2001-01-26[n年前へ]
2002-01-26[n年前へ]
2003-01-26[n年前へ]
2004-01-26[n年前へ]
■誰の中にだって佐吉はいるんだから 
マツモトさんの「強い人」とか「弱い人」とかを読みながら、こんな文章を思い出す。
（自殺した山田花子の）親父さんと話している最中、突然「藤吉-佐吉問題」というものが浮かび上がってきた。藤吉も佐吉も根本敬マンガの根本的キャラクターで、この世界は、小心で善人でいつも他人からいじめられる「藤吉」と、強烈なアッパー系でいつも自分のエゴに他人を巻き込みいい思いをする「佐吉」によって成り立っている。「どうも由美（山田花子）は藤吉は自分であると同時に、根本さんも藤吉である、と思いこんでいたフシがあるんですよ」
この話を根本敬にすると、「はーん、すると俺の中に吉田佐吉が見えて来ちゃって失望したと…。だけどね、山田花子の中にだって佐吉はいるんだから」という答えだった。
「消えたマンガ家」 大泉実成
2005-01-26[n年前へ]
2006-01-26[n年前へ]
■最初の一瞬で決まる「WEBサイトの印象」
色々なことに忙殺されて、身動きとれない今日この頃。Tech総研ブログ「平林 純@「hirax.net」の科学と技術と男と女」に、最初の一瞬で決まる「WEBサイトの印象」〜 一枚だけ目を惹く画像を使う、これがコツさ！ 〜 を書いてみました。
「内容が良いページを書いているサイトは、デザインも良いことが多い」「デザインが悪いページを作っているサイトは、内容も今ひとつ」ということなのかもしれません。 ちなみに…
■「ホーキング博士のインタビュー」
「実証と実践で宇宙に挑戦するJAXAと、イマジネーションと理論で宇宙の謎に迫るホーキング博士。アプローチの仕方は違っても、宇宙にかける強い思いに変わりはありません。JAXAの平林久教授（電波天文学）が、ホーキング博士にインタビューし、偉大なるホーキング博士の素顔に触れました」という(つまりは、私の父がインタビュアとなっている)「ホーキング博士のインタビュー」
2008-01-26[n年前へ]
■江戸時代の地図で見る「泪橋」
「泪橋」と「思川」を江戸時代の地図で眺めてみる。今の東京が、昔の海や川や沼の上に浮いていることがよくわかる。大きく姿を変えている場所もあれば、変わっていない神社や池もある。
2009-01-26[n年前へ]
■シミュレーションで学ぶ自動制御技術入門
制御工学の教科書はたくさんあって、しかもその一冊一冊が結構視点・書き方が違う。分類がすこしづつ違っていたり、言葉の定義が少しづつ違っていたり、10人の制御工学者がいれば、11種の制御工学があるのではないだろうか、と思ってしまうほどである。
」は（特に）各種PID制御を付属CDに入っている「制御システム体験ソフト」を使い納得することができる書籍である。（最近出版されている）制御工学に関する本は根こそぎ読んでいると思うが、一番最初に、制御工学を「体感する」ために買うには本書はとても良い本だと思う。
ところで、景気の落ち込みが激しい中で、景気対策として報道される内容を理解しようと思ったら、経済学と制御工学の基本を知っておくと良いような気がする。少なくとも「システム」の数的な動きというものに惹かれる人たちであれば、それでいて経済学と制御工学に触れたことがない人であれば、経済学と制御工学の本を手に取ってみることは、新鮮な経験だ思う。色んなことがどのように動き、それらを安定化させるためにどのような制御が行われているか、その制御は果たして実効性があるか、そんなことを知るには経済学と制御工学をかじっておくと面白いはずだ。
そうすれば、ニュースを、これまでとは違う視点で眺めることになるのではないか、と思う。ただし、不確かなことが多いこの世界では、歯切れ悪く単純明快ではないような感想をいつも持つようになってしまうかもしれないという、両刃の剣なのだけれども。
2010-01-26[n年前へ]
■井の中の蛙(かわず)、大海を知らず （初出：2005年09月17日）
浜辺に行くと、白い雲も少なくなって、完全に秋空になっていました。広い海と青い空を眺めていると、こんな一節が心に浮かびます。
井の中の蛙、大海を知らず
しかし、空の蒼さを知る
これは、誰かが荘子「秋水編」の有名な一節に「しかし、空の蒼さを知る」という一節を付け足したものだといいます。
井戸の中からでは、頭上に空いた丸い穴を通して、蒼い空が見えるだけです。そんな世界が限られた井戸の中からだからこそ、「空の蒼さ」を誰よりも知ることだってできることもあるのかもしれません。空しか見ることのできない井の中の蛙だからこそ、憧憬とともにその「空の蒼さ」を心に刻むことだってあるかもしれない、と思います。
そういえば、4歳の頃から6年間ほど、私は長野の野辺山高原に住んでいました。その後、野辺山高原から東京へ引っ越してから、「空が蒼くないこと」と「水道の水が冷たくないこと」に驚いた記憶があります。私がそれまで知っていた「空の色」は濃い藍色(リンク先はPDF)だったのですが、東京へ越してから見る空は「水色」でしたので、とても驚いたのでした。
長野の(少なくとも当時は)山奥で都会もろくに知らず、まさに「井の中の蛙」だったわけですが、先の詩の通り「空の蒼さ」は知っていたというわけです。
時折、自分がいる狭い世界でなく広い世界を眺めてみたい、という気持ちになることもあります。「井の中の蛙、大海を知らず」という言葉が頭に浮かぶことがあります。そんな時、同時に「しかし、空の蒼さを知る」という言葉も心に浮かびます。
あなたなら、「井の中の蛙、大海を知らず」という言葉をどんな時に思い浮かべるでしょう？そして、その言葉に「どんな一言」を続けてみたくなるでしょうか？
2012-01-26[n年前へ]
■続々？Mathematica機能を使うIronRubyコードを書いてみる
数式処理ソフトであるMathematicaの機能をIronRuby(.NetによるRuby実装)から使うRubyコードを少し書き直してみました（mathruby.rb）。具体的には、Mathematicaの計算カーネルと「やりとり」をする通訳部分に、Mathematicaから得られた値をRuby側のクラス（Array,String,Numeric 等）に自動変換するコードを付け足してみました。
このRubyスクリプトを実行するディレクトリに"Wolfram.NETLink.dll"（ここからダウンロードできるファイルを展開した中にあります）を放り込んで、たとえばこんな「２次方程式の解を求めよ」というコードを書くと、そして、そのRubyスクリプトをIronRubyから実行すると、
pp 'x^2 == 3'.Solve 'x'次のように答が得られます。
[["x -> -Sqrt[3]"], ["x -> Sqrt[3]"]]Mathematicaの計算カーネルからRubyが得る答は、もちろんRubyのArrayクラスのオブジェクトです。２次方程式の解ですから、要素が２個の配列が返されています。
あるいは、 pp [1,2,3].Sin.N というコード、つまり、配列[1,2,3]のそれぞれに「Sin関数を適用した上で、”数値化”せよ」という命令を書けば、
[0.841470984807897, 0.909297426825682, 0.141120008059867]という「数値」クラスのArray（配列）が得られます。
違う言語の間を「繋ぎ」を作ろうとすると、それぞれの特徴（売り）・個性・違いを（ほんの少しだけ）垣間見ることができるような気がして、何だか少し面白いもののです。
上記コードの動作確認は、Windows上で行っています。.Net実装であるmonoを動かしたOSX では、monoの正規表現動作不具合などにより、上記コードは動作しません(2012/01/28現在)。
2013-01-26[n年前へ]
■続 建築基準法とミニスカートの幾何学による「３５ｃｍ丈のミニスカートは絶対安全」という証明ーエスカレータ編
続 建築基準法とミニスカートの幾何学による「３５ｃｍ丈のミニスカートは絶対安全」という証明ーエスカレータ編を書きました。
さて、階段ではなくエスカレータならどうなるのでしょう？ 私たちが街中にある駅やショッピングセンターといった場所でフロアー間を移動する時には、階段でなくエスカレータを使うことも多いものです。
実は、エスカレータ上でも「３５ｃｍ丈のミニスカート＝絶対安全となる境界値」なのです。 なぜかというと…
2016-01-26[n年前へ]
■M.C.エッシャーのRelativity"を全天周で眺めてみよう!?
「手作りプラネタリウムと３D映像全国出張投影」の工房ヒゲキタさんに会いに、新宿２丁目近くの中華料理屋に行った。せっかくなので、以前から「M.C.エッシャーの立体世界を全天周プラネタリウムで眺めると面白いはず」と思っていたので、そんな雑談をするために３Dデータを（下に貼り付けた既存データを使って）作ってみた。
エッシャー自身も立体的なアート、周期的パターンが繰り返された球状の木製模型を作っていたりする。…けれど、それらは実際に眺めてみても結構つまらなく感じられてしまう。なぜかと言えば、そんな風に緻密に空間を埋め尽くしたアートであったとしても、そのごく一部しか眺めることができないとしたならば、新鮮さや面白さがほとんど消え失せてしまうからだ。
だとしたら、エッシャーの非現実かつ現実的な世界に３６０度全天周で入り込むことができればとても興味深いはず！というわけで、今朝は、幾何学的に無矛盾な "Relativity" を全天周で眺める準備をしてみた。幾何学的に無矛盾というのは、四方に配置された階段や壁は、そこに佇む人の向きが無重力で不思議なだけで、３次元空間的に特に不思議なところがあるわけではない、という意味だ。
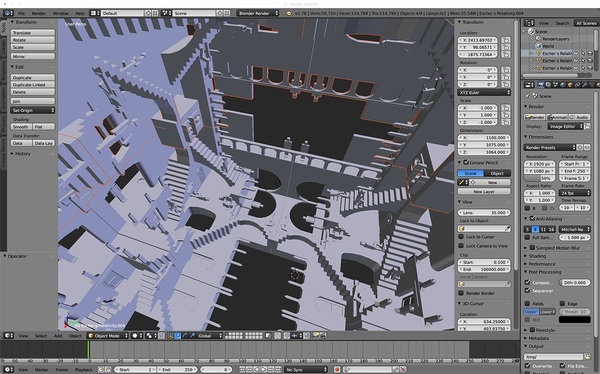
エッシャーが作り出した、非現実だけど妙にリアリティを備えた世界に入り込み、周囲の世界全てが奇妙に埋め尽くされていたとしたら…きっととても新鮮で楽しいと思う。M.C.エッシャーのRelativity"の世界は、全天周のプラネタリウムで眺めてみたら、絶対楽しいと思う。
」など。
