hirax.net::inside out::04月23日

■今日読んだ「Dreams come true」　

　進藤　「仕事で理想的なパートナーに巡り会う秘訣なんてありますか？たいていみなさん『運だ』っておっしゃるんですけど。」
　その後のドリカム中村の台詞は今発売されてる週刊アスキーの「えっ、それってどういうこと？」を読むのココロだ。それにしても、やっぱりそれは『運』じゃないよなぁ。

■円周率　

　教科書で円周率が3になるというのはデマとのこと。円周率はあくまで3.14を使うとの話。ふむふむ。 from 週刊朝日。

■今日の死兆星　

　6時〜裾野。10時に裾野出発。13時〜取手で打ち合わせ。17時取手出発。20時〜裾野でうち合わせ。諸々の作業の後24時帰宅…　夜空に輝く星、あれは死兆星か？

■ThinkpadT30発売　

　Tecra9100はデカイ。T30はパッドがちと余計。気にしなければ良いだけだけど。だけど、ちと重いかな。（リンク）

■某小説を読み通すのだ　

　寝る前のほんの一瞬に、はてなの近藤さん宅から借りてきた某小説を読み始めた。うむむ、これは…私小説なのか何なのか…。あぁ、あまりに生々しすぎるような…。読みたいような、読みたくないような…。
　というわけで、そんなこんなで時間がとれない今日この頃。

■便利ソフト　

　Windows上で現時点でのGnuPlot, GhostScript, ImageMagick, WinGraphViz, ActivePerlのインストール手順を便利ソフトにメモしておきます。手順は簡単ですから、Windowsユーザーでこれらのソフトを使ったことがない方は試しにインストールしてみませんか？どれも入れておいて損は無い(得はたくさんするけれど)ソフトばかりです。特にATOKユーザーは、これらのソフトをインストールしておけば近々とても便利な世界を手に入れることができるかも？

■道端の花　

■分杭峠「ゼロ磁場地帯」　

　分杭峠「ゼロ磁場地帯」がブーム。 from あらきけいすけの研究日誌

■Bush photomosaic of American dead in Iraq 　

　Bush photomosaic of American dead in Iraq.

■「歩いて伝わっていくこと」 その1　

　過去の富士ゼロックスの広報誌GRAPHICATIONを読んでいると、阿部謹也が「歩く文化」をめぐって算額(全国一覧)のことを書いていた。

江戸時代には、算学者というか数学者も日本中を歩き回っていましたね。これは専門の学者ではなくて、アマチュアの数学好きな(道楽)人たちです。そして、各地の神社などに数式を書いた絵馬を奉納してゆく。…誰か解く者はいないかと。そして、絵馬に書かれた問題を解いて廻って腕を磨くわけです。阿部謹也　「歩く文化」をめぐって　GRAPHICATION

■青空の"青"　

　幸田露伴の「音幻論」で言及されているという「"青"は、本来、黒と白との中間の不鮮明な色を広く表した。青、緑、藍だけでなく、灰色までも表したらしい」という一節をGRAPHICATIONの中で読む。
　「青春」とか「ブルーな気持ち」とか、色んな「青」に「黒と白との中間の不鮮明な色」を重ねてみるのも、一興か。黒から白までの幅広い色の何処かに、青という言葉を置いてみると、ふと腑に落ちることもあるかも。BGMはもちろん、ザ・ブルー・ハーツの「青空」で。

■ミクロの決死圏＠自分の鼻の穴　

　二ヶ月続いている喉の腫れを見てもらうため、耳鼻咽喉科へ。レントゲンを撮った後に、椅子に座って鼻からファイバー・スコープを喉まで入れられる。ファイバースコープの出し入れが終わったと思ったら、看護婦さんの手で座ってた椅子がクルリンと90度回転させられた。すると、そこには大きなディスプレイ。そして、撮影隊（じゃなかったファイバー経由で撮影された画面）が鼻の穴の中へと侵入していくシーンがイキナリ始まる…。あぁ、自分の鼻の穴でミクロの決死圏を眺めるのは…面白いけれど、いきなりの羞恥プレイだ…。
　関係ないけれど、「鼻」って字も「穴」って字も、何だか本当の鼻とよく似ている。「鼻の穴」なんて書くと、なんだかまるで表形文字みたい。

■ドストエフスキー「悪霊」の人間関係マップ　

　「電車の中で毎日読んでも内容把握に三ヶ月かかった」というドストエフスキーの「悪霊」を、これから読む人のために、登場する人物たちの人間関係をまとめて描いみたという「ドストエフスキー悪霊 の人間関係マップ」

■「統計はビキニ水着」で「説明文は(ミニ)スカート」の法則　

　説明文の長さに関し、実に的確なアドバイスの一つが「説明文は(ミニ)スカートだ」という言葉だと思う。

Sentence length is like a girl's skirt: the shorter the better, but it should cover the most important parts.
　（文の長さは女性のミニ・スカートのようなもので、短ければ短いほど良い。しかし、最も大切な部分はカバーしていなければならない）

　この「説明文は(ミニ)スカートだ」という言葉と良く似た表現を使って、「統計」というものをこれまた上手く現したものがある。それはこんな言葉だ。

“Statistics are like a bikini. What they reveal is suggestive, but what they conceal is vital.”
（統計というものは、女性のビキニ水着と同じだ。実に思わせぶりで意味ありげな魅力的なものがさらけ出されているがように見える。しかし、肝心な部分は隠されている）

　　Aaron Levenstein

　しかし、考えてみればこの「統計はビキニ水着」「説明文は(ミニ)スカート」といった表現は、結構何にでも使うことができるものかもしれない。
　「必要十分」が望ましいものに対しては、それがどんなものであっても「○×は(ミニ)スカートだ。長すぎても短すぎてもダメだ」と言うことができるだろう。
　また、多くの商品・技術…つまりはほとんど全てのものが「○×はビキニ水着のようなものだ。…」という風に言うことができそうだ。たとえば、"Ruby on Railsはビキニ水着のようなものだ、なぜなら…" "ダイナミックリコンフィギュアラブル技術はビキニ水着のようなものだ、なぜなら…"という具合である。
　実は、「ビキニ水着」でないものの方が少なかったりするのかもしれない。

■「高コンテキスト文化」と「低コンテキスト文化」の違い「箇条書き」　

　「高コンテキスト文化」と「低コンテキスト文化」が持つ典型的な特徴を並べたリストがなかなかに面白い。「高コンテキスト文化」と「低コンテキスト文化」の違い・特徴をリスト化したものは、派生したものがたくさん生まれている。たとえば、下に画像として貼り付けた箇条書きと、下に文章で箇条書きにしたものは、やはり少し違っている。

Low Context Communication

1. Absolute values
2. Need for precision in language - words carry explict meaning
3. Responsibility based on contract
4. Agreements written don and records kept
5. Well-timed interruptions that move the conversation forward accepted
6. Decision-making ideally logical
7. Uncomfortable with silence(indicates a breakdown of communication)

High Context Communication

1. Relative values
2. Tolerance of verbal ambiguity(non-verbal and coded communication)
3. Responsibility based on general agreement
4. Written agreements flexible according to circumstances
5. Interruptions considered rude, particularly when made by a junior
6. Decision-making allowing for feelings
7. Not uncomfortable with silence(can be communicative)

　こんな箇条書きを眺め、「（二つの文化の違いを整理した）各項目のどちらに対応するか」を確認することで、自分自身や自分の周囲の人、あるいは「集団」が、「高コンテキスト文化」と「低コンテキスト文化」のどちらのタイプに属するか、あるいはどちらの傾向が強いか、を比較・自覚してみると面白いと思う。そうすることで、コミュニケーションの中で起こる問題が「あぁ、なるほど。これは必然的に起こることなんだな」と理解できたり、その対策をとることができたりもするかもしれない。

■眠る「睡蓮（スイレン）」　

　「タンポポの花は、夜閉じる」ことが新鮮だったので、同じように夜眠る花を探してみた。すると、たとえば、（私たちがよく眺める種類の）スイレンもそういう「夜は閉じて眠り、昼には花を開く花」である、と知った。だから、「睡眠の蓮」で睡蓮と名づけられたという。

　そういうことを知ると、睡蓮で彩られた公園の池を見るとき、これまでとは違った見方をするようになるように思う。たとえば、それが昼の池なのか、それとも、夜なのかということを意識しながら眺めるようになりそうだ。

　「睡蓮」という言葉を見ると、クロード・モネを思い出す人も多いだろう。モネが一番描いたものが、「睡蓮」である。さまざまな色彩で、睡蓮が浮かぶ景色をモネは眺め、絵筆で描き出している。「光の画家」と呼ばれたモネは、光に照らされた風景がきらめくようすを、写真よりリアルに描き出している。

　睡蓮には、夜眠り昼咲く種もあれば、昼眠り夜起きる種もあるという。光を描いたモネが見たたくさんの「睡蓮」は、一体、どんな種類の睡蓮なのだろうか。それは、陽の光の下に咲く睡蓮だろうか、それとも、月光の下で咲く花だろうか。

■「黒体放射」する「自転車に乗る女子高生のお尻」　

　高校生の頃、女子高生の「制服」に心の底から憧れていました。通っていた学校は共学だったのですが、自由気ままな服を着ることができる私服の学校だったこともあり、「人（ヒト）は自分が持たないものに憧れ・好きになる」という世界の原理原則にもとづいて、それが「ブレザー」でも「セーラー服」でも「それが制服でありさえすれば、素晴らしい」という制服マンセーな太く固い背骨を得て、さらに「制服という型を守り抜く心」にこだわる精神構造を得るまでに至ったわけです。

　たとえば、建築で言えば、鉄骨建築が理系で、プレハブ住宅が文系なのである。プレハブ住宅を支えるのが壁であるように、皮膚の感覚を大事にするのが文系で、力強くそそり立つ鉄筋コンクリートのごとく、骨から組み立てていくのが理系なのである。つまり理系は骨があるのである。詩で言えば、散文詩は文系で定型詩が理系なのである。つまり、理系は型を守り抜く心を持つのである。
　だから、たとえば、理系は女子高生の制服が大好きなのである。ありとあゆる個性を持つ女子高生たちをセーラー服（あるいはブレザー）という記号で記号・集合論的に取り扱うことを可能にし、ついにはその制服を見るだけで萌えることができる、それが理系なのである。

「めがねっこ大好き。 」

　そんなわけで「女子高生の制服こそが世界の至宝の存在だ！」と信じていたわけですが、そんな風に思いつつも、ひとつだけ「これさえなければ…」と感じることがありました。その「女子高生の制服」のここさえなければ…と感じていた部分というのは、自転車通学をする女子高生は、例外なく、制服のお尻部分が実にグロッシーにテカっていたことでした。黒い色の制服が好きだったこともあって、その黒い制服に白く輝くテカリを持つことに違和感を持っていたのです。

　制服のは粗い繊維でできています。そんな制服に光があてられたとき80パーセント程度の光は繊維内部に入り・そして繊維の中で吸収され、やがて熱エネルギーに変わります。残りの20パーセント程度の光は、スカートの繊維表面で反射し四方八方に散っていきます。四方八方に散る…ということは、どこかひとつの方向に反射するわけではありません。つまり、スカートがテカって見えるということはないわけです。

　ところが、毎日自転車のペダルを漕いでいる女子高生たちの制服は、サドルとお尻で擂（す）り潰（つぶ）されて、繊維表面が真っ平らに変形していきます。表面が凸凹とした繊維からの反射光は強くありませんが（テカりませんが）、表面が平らに潰された繊維からの反射光は強く・そんな制服を育てた「女子高生のお尻」はテカり輝いてしまうのです。

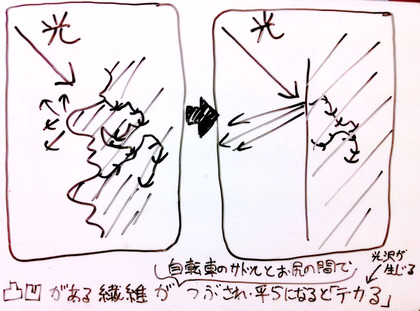
　自転通学する女子高生たちは、見るからに輝いています。そして、そのお尻もまた輝いているのです。その黒い制服が輝くようすを、極めてわかりにくく表現するならば、それはエネルギーを反映して光り輝く黒体放射にも思えます。

　ところで、女子高生の制服（スカート）は、最初から光沢仕上げの繊維で作った方が良いのかもしれない、と妄想します。最初から光沢を持っている繊維ならば、表面がもとから平滑な繊維ならば、毎日自転車に乗っていてもお尻が黒体放射してしまうこともない…と思う一方で、全身テカリまくりの制服は絶対ダメだ〜とも考えたりするのです。ということは、「自転車に乗る女子高生のお尻」は未来永劫「黒体放射」し続ける…それはそれでいいのかも、しれません。

■ぼくらが見慣れた２次方程式のグラフは…「胸の谷間」の方程式だった！　

中学生か高校生の頃、XY平面の上にy=x^2+1といった２次方程式のグラフを描き、さらにそのXY平面の上にy=0という直線を描き、そのふたつのが交点を持たないので、x^2+1=0という方程式は実数解を持たない…という説明を聞いた覚えがあります。

　けれど、２次方程式の解の公式を解けば、そのy=x^2+1という方程式は２つの解、２つの複素数の解を何処かに持っている…という説明を聞きながら、何だか腑に落ちなかったような気がします。

　先日、「複素数係数を持つ２次方程式の（複素数）解を”可視化する”エクセルシート」を作ってみましたエクセルで２次方程式の「解の配置」を図示してみる!?）。そして、x^2+1=0という方程式の解を眺めながら、ふとこんなことを思いました。

なんだ、これがぼくたちの探している青い鳥なんだ。
ぼくたちは、ずいぶん遠くまで青い鳥を探しに行ったけど…
本当は、いつもここにいたんだ。

　複素空間上に、実に単純な２次方程式が描く曲面は、ふたつの（まるで胸のような）ふくらみを見せ、…x^2+1=0という方程式こそが、人を魅惑する何よりホンモノの「おっぱい曲面方程式」だったのではないか、と思ったのです。これまでに、たくさんの「おっぱい方程式」を眺めてきたけれど…x^2+1という思春期に眺めた式こそが、本当のおっぱい方程式ではなかったか…と気づいたのです。

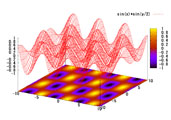
　たとえば、下のグラフは複素空間上でx^2+1という式で求められる値と０という値の間の距離（ユークリッド・ノルム）を（縦軸を反転しつつ）描いてみたものです。つまり、それはx^2+1=0という方程式への「複素空間上での解への”近さ”」をグラフにしたものです。

　i(アイ)と-i(アイ)という虚軸上に頂（いただき）、すなわち解を位置させる「ふくらみ」は、それはまさに「おっぱい曲面」を感じさせます。…というより、これが「おっぱい」でなかったら、一体何だというのだ…という姿形をしています。けれど、この「美しい曲面」は、ただ複素空間上に描かれた ”x^2+1”というだけの曲面です。

　そして、こんなグラフを眺めながら、…ぼくらが見慣れた実数で描かれたXY平面上の２次方程式のグラフは…複素空間上にあるはずの「おっぱい曲面」上に（ふたつの胸を分けるように）描かれた一本の曲線だった！…私たちが見慣れたあの曲線は「（魅惑の）胸の谷間の方程式」だった！と気づいたのです。

　たとえば、上のおっぱい曲面を２分するように描かれた黒い線こしが、黒板の上に繰り返し眺めたはずの”y=x^2+1”という、単純で見慣れた２次曲線です。

　中学生の頃、黒板の上に見た「XY平面上に２次方程式のグラフ」は「胸の谷間の曲線」であったし、その魅惑曲線の向こうには複素空間上のおっぱい曲面があった…なんて、何だか凄いと思いませんか？

ふたつの胸のふくらみは、
何でもできる証拠なの。

「魔女っ子メグちゃん」

■「ボカし処理された暗号文」の解読法を科学する!?　

　アスキーPC 6月号、「ボカし処理された暗号文」の解読法を科学する!?が届きました。内容は、いわゆるボカし処理としてガウシアン分布のボカし処理が広く用いられる理由や、そんなボカし処理された画像を「なるべく戻してシャープにする」ための方法を書いたものです。

　『読者への挑戦状！この「暗号」を解き、名探偵になってみろ！？』の「暗号」も、ガウシアンボカしが掛けられた画像です。だから、この「暗号」を解こうと思ったら、まずは「ボカしをなるべく戻す」作業をすることになります。…だから、「ボカし処理された暗号文」の解読法を科学する!?を（本屋で見かけたら）少し読んでみると良いかもしれません。

　ちなみに、『読者への挑戦状！この「暗号」を解き、名探偵になってみろ！？』の「暗号」は、画像が大幅にボカされているため、ボカしをなるべく戻したとしても、そこに書かれた「文章」がわかるほどにはなりません（下に貼り付けたのが、ボカしを”ある程度”取り除いてみた例ですが、まだまだボケています）。そこで得られた「手掛かり」をもとにして、「その条件に当てはまる文章を選び出す（見つけ出す）」という作業を行うことになります。

　というわけで、　次回、アスキーPC連載記事の最終回で解き明かす・相手にする「暗号画像」が実は『読者への挑戦状！この「暗号」を解き、名探偵になってみろ！？』の画像です。たとえば「解くための持ち時間を４５分」というように決めて（制限して）、集中して「解読」に挑戦してみると面白いと思います。

　（解答が出たら正誤確認は、こちらかこちらまで、「解答・推理」を御連絡下さい）

■国土地理院ドローンヘリ映像から、阿蘇大橋近くの３次元地形図を生成してみる…。　

　福岡県西方沖地震の後に、国土地理院がドローンヘリで撮影した動画を元にした３D地形図が公開されている。撮影動画自体もYoutubeで公開されているので、その動画を使って（自分でも）撮影されている風景の３次元形状復元をしてみた。たとえば、下のレンダリング画像は、得られた３次元メッシュを（モデラ・レンダラの）Blenderでレンダリングしてみたものだ。

　また、自分で３次元形状を生成してやれば、さらに下に貼り付けたような（国土地理院が提供している３Dマップより）高解像度な形状を得ることもできる。そのようにして得られた３次元の世界を、たとえばヘッドマウントディスプレイ（HMD）で立体視したりすれば、土砂の流れもわかりやすく感じられる。

　今や、簡易なフルカラー３次元空間程度のものであれば、スマホで撮影した動画や、TVで流れているような誰かが撮影した空撮動画などからでも、誰でも作れる時代だ。

■Ricoh Theta用の極座標自動ステージを作ってみよう！（その心は、どちらもRなθと解きます）　

　これまで、今や誰もが持ち歩いているスマホを使った手持ち移動撮影で、大径レンズを取り付けたカメラにような画像を作り出してみたり（「手持ちスマホ撮影動画からの超巨大開口レンズ撮影」に挑戦してみよう!?　）、あるいは、全天周を撮影することができるRicoh Theta Sカメラを使って、ありとあらゆる情報を手に入れてみようと遊んでみたりしてきました（Ricoh ThetaSで全天周／HDR／立体動画の撮影に挑戦してみる、Ricoh Theta S 撮影動画で３次元の世界を撮影してみよう!?）。

　今日は、それらの続きをやってみよう！というわけで、全天周カメラRicoh Theta用の極座標自動ステージを作って、いくつかの撮影＆後処理を行ってみました。

　まず、左下は試行錯誤的に作っている（途中の）自動制御ステージです。ステージを動かして違う場所から撮影した写真を使えば、もちろん立体的な映像を作り出すことができます。…というわけで、試しに作った立体視用画像が右下の画像です。

　２つの視点から見た映像を並べれば立体的な映像を感じることができるのと同様に、複数視点からの撮影画像を解析すれば、立体的な世界を再現することができます。…というわけで、自動制御ステージに載せたTheta Sで撮影した画像から生成してみた３次元映像が、下に貼り付けた動画です。

　…と、Ricoh Theta用の極座標自動ステージを作りながら、ふとと気付いたことがあります。それは、もしかしたら、あまり目的思考がなく、Ricoh Thetaを使ったRθな極座標系ステージを作ってみたかっただけかもしれない…ということです。（その心は、どちらもRなθと解きます）