hirax.net::inside out::06月21日

■スパイダー　

かまやつひろしからの連想ではなくて、動き回るスパイダーでもなくて、WEBサイトって雲の巣みたいなところがあるなぁ、と。キャバクラ(行ったことないけど)のお姉さんもそんな感じなのかな。

■青い空とビルと緑　

　新宿からICCに行く途中。（リンク）（リンク）

■美少年　

　で飲んだ。単なる大セクハラ大会になった…。今日の結論。「オッパイの主観評価、計測、定量化の三本柱で攻めるべし」

■武蔵新田　

　下丸子からでなくて、武蔵新田経由で行ってみた。駅前の昔ながらの店の感じがとても良い。いつかあそこら辺を散歩し直すと誓うのだ。

■貧血オン・ザ・コダマ　

　で、帰りの新幹線の中で貧血になった。顔が冷たい。ビックリだ。

■art.bit collection　

　私の好み的にはきっと面白いはず、と考えてICCに行った。面白かったのは"sand"と"sodaplay"くらいだった。これまで"sodaplay"は私は曽田さんが作ったと思いこんでたので、その誤解を直せたのが唯一の収穫か。
　しかし、あの係員の多さは犯罪的ですらあると思う。観客一人に対して８人位の係員がいた。あれだけ多いと、かなり不愉快な感じを受ける。（リンク）

■木もれ日プロジェクト　

　表参道 スパイラル。通路に置いてある三点ほどの展示。とても良かった。近くを通るなら、ぜひ行くべし。（リンク）

■文の長さは女性のミニスカート　

　今日見た素晴らしい名言。

Sentence length is like a girl's skirt:the shorter the better, but it should cover the most important parts. 文の長さは女性のミニスカートのようなもので、短ければ短いほど良い。しかし、最も大切な部分はカバーしていなければならない。

■今日の連絡　

　確か、去年は印刷所との打ち合わせで電話をしまくり、私用の電話とは別の領収書をもらうのが面倒で、結局二万円ナリの電話代金を自腹切ったような…。というわけで、今年もどうなることやら…。
　というわけで、環境設定が終わりました。連絡いつでもつきます。

■小田原駅の東海道線ホーム　

　三島発7:00。武蔵小杉発12:40。新横浜発13:15。小田原駅で新幹線が止まる。運休ではないけれど、当分発車のメドが立たないというので、東海道線に乗り換えて三島着15時過ぎ。箱根中腹に着くと、16時近く。
　小田原駅で東海道線を待つ間に、とりあえずパノラマ写真を撮ってみた。昨日のパノラマ写真と比べてみると、昨日西の空に感じた台風が確かに進んできていることがわかる。

■All the Colors of the Rainbow 　

ほら、…このブローチには、この世の中の全ての色が含まれている。このブローチのガラス、実は透明なんですよ。よくよく見れば、色なんてついていない

■裾野　

　たまに、「裾野って裾野市だったんですね」と言われます。「裾野」というのは地名です。箱根山の麓、冨士の裾野を見下ろすそんな場所です。

■Mathematica用統合開発環境Wolfram Workbench　

　MathematicaなどWolfram社の技術向け総合開発環境のWolfram Workbench. ソースコードエディタやデバッガ、さらにはプロファイラ・バージョン管理システムなど、重宝しそうな機能がたくさんある。Mathematicaを、最初のアイデアスケッチで使うことが多い私のようなユーザでも、重宝するだろうか…？どうだろう？

■オムニホイールで理想の「パック」を作ることができるか!?　

　「"オムニホイール"で理想の"ホッケー・パック"を作ることができるのだろうか!?」と、ふと考えた。氷の上でも、専用リンクの上でもなく、普通のアスファルトの上で滑らかに自然に動くホッケー・パック"を、"オムニホイール"を使えば作ることができたら良いな、と考えた。

　オムニホイールというのは、(omini=全方向)ホイール=車輪、つまり方向性を持たないというか全方向に進むことができる車輪である。オムニホイールを使った台車の動き(動画)などを眺めていると、極小オムニホイールを使い、さらに姿勢検知・駆動制御を極限まで駆使したならば、「まるで氷の上を滑って行くかのような自然な動きを(アスファルトの上で)するパック」を作ることができたりはしないだろうか、と考えたわけである。

　逆に言えば、そんなメカ搭載のパックが欲しくなるくらい、自然なパック操作をすることができなくて、悩んでいるということである。アスファルトの上でパックを打ってみても、進ませようとする方向にパックが上手く動いてくれることはほぼなくて、いつも思ってもいない方向に(ヘロヘロと)飛んで行ったりする。それどころか、飛ぶこともなく、コロコロと転がっていってしまうことも多い。

　理系心は気温とゴムとアスファルトの変形と…とかのせいにしたくなる。もちろん実際には単に下手だから、である。しかし、やはり、理系心はそんな物性変化のせいにしたくなったりするわけである。

　そこで、これなら、思った方向に飛ぶようなパックを作った方が早いのではないか、と思ったわけである。ざっと計算してみると、一個百万近くになりそうだけれども、そんな「（どんな状況でも）自由自在に特性を変えることができるパック」を作ってみたい今日この頃だ。

■Mathematicaライブラリをさらに「オブジェクト指向風」にしてみました　

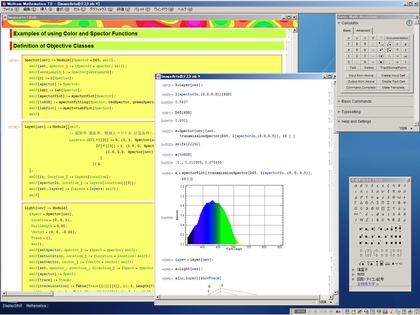
　以前、分光スペクトル・色処理用のMathematicaライブラリ（関数群）を作りました。そして、この前Mathematicaで「オブジェクト指向風」記述をすることで、括弧の対応や処理手順を見やすく・わかりやすくしてみました。もちろん、「わかりやすい」というのはあくまで主観的な話です。

　今日は、もう少し本格的な例を作ってみようと考えて、そのMathematicaライブラリに、Spectorクラス・Layerクラス・Lightクラスを作成・追加してみたのです。物体を光で照らした時に見える分光スペクトルを、モンテカルロ的に解く機能を適当に付けてみました。

　そんなわけで、スペクトルを扱うSpectorクラス、立体形状を扱うLayerクラス、そして、適当に光追跡を行う機能を盛り込んだLightクラスを仕立ててみたのです。

　たとえば、デフォルト設定をそのまま使うなら、

layers=Layer[new]
aLight=Light[new]
aLight[in,layer][showTrace]

　あるいは、

Spector[new][set,blueSpector][spectorPlot]

そんなわけで、数日後には、バグ確認・使い方の例などを加えた上で、サイトからダウンロードできるようにします。また、適当に仕立てたこのツールを使い、何か解析でもしてみようと思います。

■エクセルのグラフをマウスでグリグリ動かしながら赤青メガネで飛び出す立体動画で眺めよう!?　

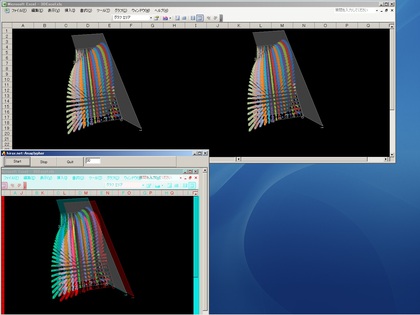
　マイクロソフトのエクセルでチャート（グラフ）を作り、そのチャートをコピーして同じチャートをふたつ横に並べさえすれば、それを外部からマウス操作で自由自在に動かしつつ・アナグリフ立体動画として眺めることができるソフトを作ってみました。その動作のようすが、下のようになります。三次元グラフをマウスでグリグリ動かしつつ（しかも複数グラフを同時に）、さらに、赤青メガネ（アナグリフ）立体画像として眺めることができてきるのがわかると思います。

　この上の動画では、画面上半分にエクセルの画面があり、左下に作成したソフトが表示している（赤青メガネ用の）立体画面があります。赤青メガネ用立体表示祖をしている画面の部分でマウス操作をすれば、立体グラフを自由自在に動かすことができる、というわけです。

　エクセルでは、残念ながら、あまり三次元的に意味のあるチャートを作ることはできません。たとえば、下のグラフはExcel 2010で作った三次元チャートですが、今一つ立体チャートのワクワク感を楽しむことができるようなものではないように思います。

　しかし、どんな道具も使う人次第ということもあるわけですから、うまくエクセルを使いこなせばきっと面白い立体的なチャートを作り出すことができるように思います。面白く・新鮮な立体グラフを、簡易な立体ディスプレイであるアナグリフ表示でリアルタイムに色々眺めることができれば、きっと面白いのではないでしょうか。

　今日作ったソフトは、ここに置いておきます。エクセルのグラフを外部から操作するソースコードのポイントは、近く、適当にまとめて公開しておきます。

■解析解より「数値シミュレーション」を好む人がいる理由　

　私は「因果関係に落とし込みづらい数値シミュレーションより、（可能であるならば）解析解の方がよっぽど使いやすい」と考えています。数値シミュレーションは、極論に言えば「こういう条件なら、こういう結果になった」「こうしたら、こうなるらしい」というものにすぎないので、「もたらしたい結果を実現するためには、どういう条件にすべきか」といった逆問題、私たちが日頃考える「どのような選択をすべきか」という問題を解くためには、「うまくない」方法であるわけです。解析解は単純明快に因果関係と対策を与えてくれるのに、数値シミュレーション結果はそれを眺めて頭を悩ませなければなりません。

　けれど、そんなことが「常識でなかったり」もします。解析的に解けるようなことに対して、（信頼性がどれだけあるかもわからない）数値シミュレーションをなぜか好んでしてみたりする、という話も非常に多くあります。「そんなことは数値シミュレーションをするまでもなく、○だから×で△になるのは当然ではないか」という印象を抱いてしまう数値シミュレーションを眺めることも多いものです。

　たいていのことには、「納得しうる理由」があります。だから、解析解より「数値シミュレーション」を好む人や組織が多いのには理由がある、と私は思っています。ここでいう「理由」というのは、「解析解を使える状況下であっても、数値シミュレーションの方を重宝がる人を作り出す」理由です。

　そこには理由があるはずだ…とも思っているのですが、その理由をなかなかシンプルに見つけ出すことができずにいます。…ひとつのポイントは、「解析解が単純明快に因果関係と対策を与えてくれる」ことに対して、その「単純明快さ」「頭を悩ます余地が少ない」ことにあるのかもしれない、とも考えています。…が、よくわかりません。

　解析解より「数値シミュレーション」を好む人がいる理由、それは一体どんなものなのでしょうか？

■「ケーニヒスベルクの橋渡り問題」 藤沢・江の島"境川サイクリングロード" 編　

　天才オイラーが解き明かした「バルト海沿いにあるロシアの街ケーニヒスベルクで、街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、（どこでも良いから）スタート地点に戻ってくることができるか？」という”ケーニヒスベルクの橋渡りの問題”」は、私たちが日々過ごす街にも溢れています。

　たとえば、神奈川県は川崎・鶴見の辺りにある『街で見かけた「ケーニヒスベルクの橋渡り問題」』や、あるいは京都の町で「鴨川源流で眺める理系風デート」…といったように、どんな町にも一筆書き問題は潜んでいるのです。

　今日は、東京都町田市近くから神奈川の江の島に流れる「境川」に掲げられていた「ケーニヒスベルクの橋渡り問題」を眺め・挑戦してきました。これまでに挑戦した「橋渡り問題」の中では、最も橋が多く・距離も長い…巨大な「一筆書き・橋渡り問題」です。

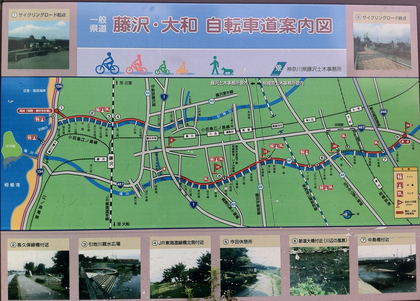
　ところで、境川の「ケーニヒスベルクの橋渡り問題」は、江の島を領域に入れてしまうと、「一筆書きできないことは自明」です。何しろ、地図上は橋がひとつしか無いので、江の島は「その場所をスタート地点としたら、戻って来ることができない、けれど、通過することもできない場所」であることが明らかだからです（本当は、江の島には橋が２本かかっているのですけどね）。

　…かつてケーニヒスベルクと呼ばれたバルト海沿いのカリーニングラードという街に、「江の島」のような島があったとしたら、オイラーのような天才でなくとも、容易に「ケーニヒスベルクの橋渡り問題」を解き明かすことができたのかもしれない、一筆書き問題が成立するための条件をいともたやすく気づいたのかもしれない、と想像したりします。

　これが、今日眺めた「理系の散歩道」です。

■立ちション後に体がブルッと震える原因は「おっしことして熱エネルギーを放出するから」じゃない!?　

　『立ちション後に体がブルッと震える原因は「おっしことして熱エネルギーを放出するから」じゃない!?』を書きました。

　あなたは「立ちション後に体がブルッと震える」経験があるでしょうか？その経験をするのは立ちション時？それとも、座りション時？…そして、そんな現象を起こす発生過程はどんなものだと思いますか？

■NP困難？な「点を結んでいくと絵が浮かび上がる」新ルールのコネクティング・ドット　

　点を結んでいくと（たとえば数字の順番にしたがって点を純に繋いでいくと）、次第に一枚の絵が浮かび上がってくる…コネクティング・ドットが好きだ。なぜかというと、意味なくばらまかれた点を、ひとつひとつ、今いる点から次の点へとただ辿っているうちに、いつの間にか何かしらのものが描かれていく、というのが人生そのものみたいで面白いからだ。

　そんなコネクティング・ドットで、たとえば明暗の階調（グラデーション）豊かな絵を細かな場所ごとに表現しようとすると、ひとつの問題に行き当たる。それは、濃い部分は密集した線で描かれることとなり、当然のように、そうした部分には（線を繋ぐための）点が密集する。…すると、密度バラバラにばらまかれた点群は、それだけで「何が描かれているか」わかってしまう（下左図）。そして、それどころか、その点群を線で結ぶと、絵はわかりにくく・汚くなってしまうのだ（下右図）。

　そこで、 Bob Bosch and Tom Wexler たちが考え・行った研究が When the Mona Lisa Is NP-Hard（モナリザがNP困難になる時）に紹介されている。彼らは、新たなコネクティング・ドットの「ルール」、「規則正しく配置された点群を、一筆書きしつつ通過しながら、目的の絵に一番似るような全景を描き出すルートで通っていく」というものを考えてみたのだ。たとえば、左下のような規則正しい「格子点」の上を、目的を思い浮かべながら描いていくと、右のような一枚の絵が浮かび上がってくる。

　本当は、意味なくランダムに見える点群を、ただ目の前の次の点へと辿った結果として、一枚の絵が浮かび上がってくる方が（人生に似ていて）好きだ。…けれど、人によっては、自分の目標を心に描きつつ、無味乾燥とした格子点の上に、自分の足で何かを描いていこうとする人もいるかもしれない。そんな人の好みを考えると、こんなコネクティング・ドットも面白いかもしれない、と思う＊。