hirax.net::inside out::11月05日

■今日の景色　

　ちょっと散歩しに行く。（リンク）（リンク）（リンク）

■波の音　

　巨大1.9MB。高速回線使ってて海の音を聴きたい人のために。QuicktimePlayerでないと画像の再生はされません(画像の方は全然変化しないのでまぁいいけど)。FinePix4700Zで撮影したMotionJPEGの画像から、音声だけ抽出する簡単な方法をどなたかご存じありません？音声自体は小さいのになぁ。（リンク）

■彼のメールを読むとカチンときてしまう　

　「引用メールは冷たく感じる」という記述を以前も見かけて、ウムム？と意外に思った覚えが。ビジネスメールでは引用無しでは何の件だったか思い出せないことだってあるぞ、と。
　それに、逆にカチンとくる方は仕事の相手に何かそれ以外のものを期待しているのか？と不思議に思ったりもする。　from お笑いパソコン日誌（リンク）

■No side　

　そしてまた、「水に流す」と言葉の英訳にふさわしいのは"let bygones be bygones"ではなくて"No side"だということに納得し、さらにそれは「何処でもないトコ」と勝手に意訳してみるのも良いのかな、と思ったのだった。

■Photoshopプラグインぼちぼちと　

作ってはいるのですけど、なかなか「できたかな?」を更新できていません。ので、明日辺りせっせと書いてみます。

■hirax.net内のユーザーページご紹介　

　サーバーwww.hirax.net内には実はユーザーページとして黒谷明美さんが作成しているDr.Hiraxのページがあるわけです。で、そちらのページを知らない方のためにそこへのリンクを貼っておきます。
　横に貼り付けてみた絵は黒谷明美さんが描いた「少女時代の黒谷明美さん」です。だんごむしと戯れているようです。小さい頃から生物が好きだったわけですね。これは、「絵でわかる細胞の世界」（講談社）の中で使われた挿絵です。

■近況報告　

　指摘して頂いているページの記述を直せなかったり、Flashのアドバイス(?)を頂いた方にお礼をできていない、とか、メールの返事をずっと書けていなかったり、とかいろいろあります。ごめんなさい、なかなか時間が作れません。

■NTTデータ、大規模な無料Blogサービスをスタート　

　というZDNetNews。約1万人の参加を見込む大規模なもの、とのこと。

■Andy Warhol's Marilyn prints　

　これは何だかはまってしまうAndy Warhol's Marilyn prints自分の色にマリリンモンローを染めてしまえ。そして、Andy Warholの言葉だって聴くことができる。 from cat@log。

■「恋愛の磁場」「神経ネットワーク」「磁場反転」　

　「恋愛の磁場」「神経ネットワーク」「磁場反転」そんなキーワードで興味を惹かれる人は読んでみると面白いだろう「恋愛脳」
　認知科学を学ぶ書き手が「神経生理学」について考えるうちにたどり着いた結論が「性愛と想像性の先にあるのが恋愛かもしれない」ということ。そして、書き手は呟く、「恋愛って一つの創発現象かもしれない」と…。さらに下に示す文章を読んで「書き手の頭に電波が飛ばされていのでは？」と考えてはイケナイ。頭に強い電波、すなわち強い電磁波が押し寄せてくるのが、それがすなわち恋愛なのだから。

神経線維に「恋愛」という情報刺激が流れると、イメージをフェアライト・コアにして電磁石が出来て、相手への思いという強い磁場を発生させてしまう…

■「毎日の記録と想い出の写真」編　

　Tech総研で「毎日の記録と想い出の写真」にまつわる「携帯電話は体の一部／家族の想い出がDVDで蘇る／他」が公開されています。ちなみに、最初は『「肉体？の一部」と「写真の記録」編』だったものですね。というわけで、「男と女にまつわる科学？ニュース」は今回はお休み、です。

■紙風船で作られた地球儀　

　堅い「地球儀」をクルクル回すのはとても簡単。だけど、それが「地球儀紙風船」ならどうだろう？そっと、抱えて扱わないとダメだろうか、それともポンポンと叩いている内に自然に膨らんでくるものだろうか？空気が抜けない地球儀ならば、チャップリンが演じるヒンケルのようにそれを強く掴むのも良いかもしれない。しかし、紙風船で作られた地球儀はどう扱うのが良いだろう？
　そんなことはさておきも、やっぱり欲しくなる紙風船で作られた地球儀。

■ホチキスサイズの簡単ミシン　

　ホチキスと区別がつかないほどのホチキスサイズの簡単ミシン。持ち歩かなくても、一個持っておくと便利かも、の2625円ナリ。本格派のほんぬいハンドミシンですら8400円ナリ。

■ブラウザで眺めてるURLを記録し続けるアプリ　

　GPSで「自分が現実世界でいる場所」「自分が現実世界で眺めている場所」を記録し続けるCGIを作ったので、今度は「自分がブラウザ画面で眺めている場所」「自分が仮想世界で眺めている場所」を刻々と記録(表示)し続けるアプリを作ってみたくなった。昨夜、サウナ＆露天風呂で休んでいるうちにそんな気持ちがとても強くなったので、今朝作ってみた(BrowerHistoryt051106.lzh 343KB)
　動作環境は（多分）Windows 2000/ XP上のInternet ExplorerとSleipnirとFirefoxで、タブ・ウィンドーにも対応させてあり、タブ切り替えもちゃんと追跡するはずだ。（Firefoxではまだちゃんと追従させていない）　これで、自分がいつ何を眺めているかがわかるかも。

■フリー・クライミング　

■昔の野球は、バッターに今よりずっと近い位置にピッチャーがいた　

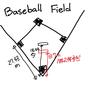
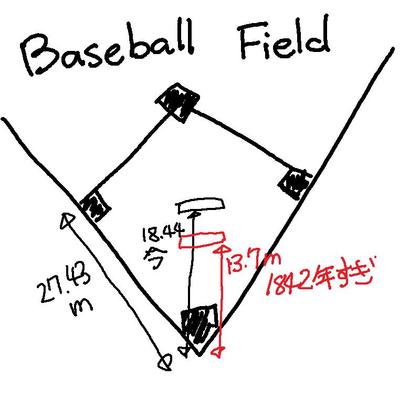　(「ダイアモンドの中心にピッチャーマウンドがあるか？」の続きです)「野球」のルーツには色々な意見がるが、現在の野球ルールの大部分は、1842年頃にニューヨーク市内の紳士クラブが作った「ニューボッカーズ・ベースボール・クラブ」という社交クラブから始まった、と言われている・・・という。「ニューボッカーズ・ベースボール・クラブは、各ベース間の距離を決めた。それが90フィート(27.431m)である。それは、今の野球規則で定められている距離と同じだから、つまり、野球場の「ダイアモンド」は一世紀半以上大きさが変わっていない、ということになる。

　しかし、ホームベースとピッチャー・プレートの距離は違う・・・らしい。書籍を調べていくと、「ニューボッカーズ・ベースボール・クラブ」が作ったルールでは、その距離は45フィート(13.7m)だったという。つまり、今より5m近く短いのである。ということは、ピッチャーは「ダイアモンド」の中心より遙かにバッターに近い位置で愛を叫んでいた、ということになる。

　それから数十年後の1881年に、ホームベースとピッチャー・プレートの距離は50フィート(15.24m)に変わり、そして、それからすぐの1893年に18.44mという現在と同じ距離に変更されたのである。ここで、ようやく「野球場のダイアモンドの中心近く」がピッチャーの位置となったのである。

　まだまだ、キャッチボール（というよりピッチング）にしかはまっていないのだけれど、ピッチングのテキストを読みあさったり、野球経験者にアドバイスを受けていると、野球の沼の奥の深さにはまりまくる今日この頃だ。

■無料のMathematica Player + IronRuby でグラフィック出力　

　無料のWolfram Mathematica Playerに付属のMathematicaカーネルではグラフィック出力ができず、グラフ描画や各種グラフィック機能を有効利用するための方法を試行錯誤していました。そんな中、「Mathematica Player+IronPython関連記事」中の、無料のMathematica Playerで画像を出力してみた（IronPythonで）」で実に技術を駆使した方法で、その問題が解決されていました。

　基本的な計算は、Mathematica Playerに付属するMathematicaカーネルにやらせ、その結果を画像にするRasterize部分を、Mathematica Playerにやらせる、そしてその結果を.NET/LINKで「操作スクリプト」に送りつける（スクリプト側はデータを受け取る）という、具合です。こういったスクリプトをさらりと書けるようになりたいものです…。

　さて、というわけで、IronRubyで同様のことをしてみました。まずは、クラスなどは作らず、ただ単に「（ネットワークからの）データ取得→計算・画像作成→Windows上でフォーム上に描画」ということを順を追って行うスクリプトを書いてみました。それが、下になります。

# c.f. http://boxheadroom.com/2009/10/30/mathematica_ipy_image
# c.f. http://d.hatena.ne.jp/arikui/20070918/1190050541

com='ExampleData[{"Geometry3D","Beethoven"}] '
width=1000

include System
require 'System.Windows.Forms'
require 'System.Drawing'
require 'mscorlib'
require 'Wolfram.NETLink'
include Wolfram::NETLink

kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
kernelLink.EvaluateToInputForm(
   '$ct={{0,0,1},{0,1,0},{1,0,0}};',0)
tmpl='$im=Rasterize['+com+
    ', ImageSize->'+width.to_s+',Background->Black];'
kernelLink.EvaluateToInputForm(tmpl,0)
k=kernelLink.EvaluateToInputForm(
    '$im=ImageData[$im,"Byte"];',0)
k=kernelLink.EvaluateToInputForm(
      '$im2=$ct.#&[#]&/@#&/@$im;',0)
kernelLink.PutFunction(
        "EvaluatePacket",1)
kernelLink.PutSymbol("$im2")
kernelLink.EndPacket()
kernelLink.WaitForAnswer()
ret=kernelLink.GetObject()

height=ret.length/width/3
form=System::Windows::Forms::Form.new()
form.width  = width
form.height = height
graph=System::Windows::Forms::PictureBox.new()
graph.width=width
graph.height=height
graph.top=0
graph.left=0
graph.image=System::Drawing::Bitmap.new(
       width, height)
height.times{|y|
 width.times{|x|
  color=System::Drawing::Color.FromArgb(
             255,ret[y,x,0],
             ret[y,x,1], ret[y,x,2])
  graph.image.SetPixel(x, y, color)    
  }
}
graph.Refresh
form.controls.add(graph)
form.ShowDialog()

　ところで、Pythonのコードを読むのは初めてだったのですが、何だか知らない言語を読むというのは「違った視点」を感じるような気がして、新鮮なものですね。

■「虹のトンネル」を時速40kmで追いかける　

　あまり意識することはありませんが、虹（主虹）の内側は明るく光っているものです。たとえば、下の写真では、道の先に虹がありますが、その虹（主虹）の内側がぼんやりと白く光っていることがわかると思います。まるで、車でトンネルの中を走っていて、その走る先に明るいトンネルの出口があるようにも見えてきます。

　こどもの頃、虹の麓にたどり着こうと、自転車に乗って虹を追いかけた記憶がある人は多いと思います。あの頃、私たちはカラフルに彩られた虹のアーチだけでなく、無意識のうちに、虹の内側に光り輝くトンネルの出口に向かってペダルを回していたのかもしれません。

　ふと、こんなことを考えました。・・・虹を見るのは、午後の夕立があがった後であることが多かったと思います。つまり、西の空が晴れて太陽の光が差し込み、東の空には雨雲と雨粒があり（雨粒がないと虹は見えませんから）、その東の雨粒に重なるように虹が浮かんでいる、という状況です。私たちは西の空の太陽を背にして、東の空に浮かぶ雨粒と虹を追いかけていたのです。

　日本の空は偏西風に支配されています。西の空から東の空におよそ時速40km程度の風が吹き、雲もそして天気も、空に浮かぶものたちは、その速度で移ろって行くのです。

　ということは、虹を映しだしている東の空の雨雲（雨粒）も、時速40kmで東へ東へと去って行ってしまうのです。こどもの私たちが、いくら必死に自転車のペダルを漕いでみても、すぐに引き離されてしまう速度です。しかも、太陽と雨雲（雨粒）とわたしたちの位置関係が、特定の幾何的関係でなければ虹を見ることはできませんから、雨雲が移動してしまうと虹も見えなくなってしまいます。つまり、東の空に浮かぶ虹には、その下にたどりつくことはもちろん、虹や虹のトンネルを見続けることすら難しかっただろう、ということに気づくのです。

　けれど、不思議なことに、こんなことを知ってからの方が、さらに虹に向かって自転車を走らせてみたい、と思うようになりました。いつか夕立が止んだあとの東の空に虹が浮かんでいるのを見つけたら、その虹のトンネル出口に向かって、（FUNKY MONKEY BABYSの「そのまんま東へ 」でも聴きながら）東へ東へとペダルを漕いでみたいと思います。「虹のトンネル」を時速40kmで追いかけてみたいのです。

■「Wolfram CDF PlayerをMathematicaとして使う方法」をRubyでもっと簡単にしてみた　

　「Wolfram CDF PlayerをMathematicaとして使う方法」を、Rubyコードを書くことで「もっと簡単」「わずか３ステップ」にしてみました。

　Wolfram Mathematicaはプログラミング言語であり、優れた開発環境です。数式処理言語としてスタートしたMathematicaですが、今では汎用言語と言っても良いくらいに、さまざまなことができるようになっています。

　しかし、そんなMathematicaの「玉にキズ」な点が「お値段」です。Mathematica を趣味で使う人たちのために295ドルで「Mathematica ホームエディション」が発売されています。今の円相場なら295ドルは２万３千円ほどになりそうなものですが、残念ながら、日本では（消費税を含めて）７万３５０円とかなりのお値段になってしまいます。

　そこで、出てくるのが「Mathematicaで作られた「処理アプリケーション」を実行させることができるWolfram CDF Player（かつてWolfram Mathematica Player と呼ばれていたもの）で、汎用的な計算をさせよう」という要望です。無料で配布されているWolfram CDF Player はMathematicaで作られたコードを実行することができまずが、ユーザが任意の数式を入力して処理させることはできません。しかし、そんな”再生専用”MathematicaであるWolfram CDF Playerは、基本的にはMathematicaと同じ処理エンジンが組み込まれていますから、このWolfram CDF Playerに任意の処理をさせてしまおうというアイデアです。 （ここでは触れませんが、CDF PlayerはMathematicaで作られたアプリケーションを実行しているに過ぎない、という点もライセンス上実は重要なポイントです）

　「Wolfram CDF PlayerをMathematicaとして使う方法」は「”決まったURL”から数式を読み込み、その数式を処理するプログラムをMathematicaで作り、そのプログラムをWolfram CDF Playerで再生させる」というアイデア・実装です。このアイデアのポイントになるのは、Wolfram CDF Playerは「”決まった一定のURL”から数式を読み込む」という「非任意」の処理をしているように見えて、実は”そのURL”が出力する数式を任意に変化させることで、任意の数式処理をさせてやる、ということです。「入力した数式をサーバに記憶させ、そのサーバからWolfram CDF Playerが数式を読み込み・処理を行う」という手順で、任意のプログラムをWolfram CDF Playerに実行させることができます。

　しかし、「Wolfram CDF PlayerをMathematicaとして使う方法」で書かれている「ローカル・コンピュータに、PHPをインストールして・HTTPサーバを動かす」という手順は少しばかり面倒です。そこで、Rubyで同じことをもっと簡単にさせることができるコードを書いてみました。つまり、与えられた数式を記憶し・返すというWEBアプリをRubyで書いてみたのです。

require 'webrick'
include WEBrick

contents = ''
s=HTTPServer.new(:Port=>80, 
                 :DocumentRoot=>'')
s.mount_proc("/shutdown"){s.shutdown}
s.mount_proc("/"){ |req,res|
  res.body = 'Work!?'
  if req.query['body'] 
    contents = req.query['body']
    res.body = req.query['callback'] + '.()'                    
  else
    res.body = contents if contents != ''
  end
}
trap("INT"){ s.shutdown }
s.start

ruby math.rb

　Universal Mathematica Manipulator 3の左側の領域で数式を入力し”TAB”キーを押します。すると、（Rubyで書かれたローカルで動く）HTTPサーバがその数式を記憶します。そして、右側の領域で"eval"を押せば、ブラウザに埋め込まれたWolfram CDF PlayerがRuby HTTPサーバへと数式を探しに行き、結果として、任意のMathematicaプログラムを処理した結果が実行される、というわけです。もちろん、前もって、Wolfram CDF Playerをダウンロード＆インストールしておくことも必要です。

　下の画像は、Universal Mathematica Manipulator 3とRubyで書いたWEBサーバで下記コードを実行させてみた際の実行結果です。音楽教室の必需品、ルートヴィヒ・ヴァン・ベートーヴェンの姿が浮かび上がります。あなたなら、どんな風に遊んでみたくなりますか？…やることは簡単「Wolfram CDF Playerのインストール・Rubyコードのコピペ保存＆実行・そしてUniversal Mathematica Manipulator 3にアクセスする」のわずか３ステップです。

ExampleData[{"Geometry3D","Beethoven"}]

■日常生活で役立つ数学の問題「マンション駐輪場割り当て数の将来予測」編　

　マンションの理事会や管理委員の役職番が回ってきたりすると、マンションの駐輪場の「割り当て数」について頭を悩ませたりすることがあります。たとえば、面積が限られているスペースに、自転車置き場とオートバイ置き場を作らねばならない…けれど、その比率は一体どのようにしたら良いかわからない…といったこともあると思います。

　あなたが住んでいるマンションが、１００戸入居できる新築マンションで、けれどまだ10世帯しか入居しておらず、その入居済み10世帯の中でオートバイを持っているのは１世帯でたった１台だけだったとします。

　残り90戸の入居がまだ行われていない現時点で、「バイク置き場」の個数を決めてしまわなければならないとしたら、あなたは一体何台程度バイクを置くことができるようにしたら良いものでしょうか？

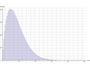
　「世帯はバイクを１台しか持つことはない」ものとして、"10世帯の中でオートバイを持っているのは「1世帯たった１台」だけだった"ということをもとにして、世帯がバイクを持つ確率pの（さらに）確率分布を(逆算して)求めてみたのが下のグラフです。

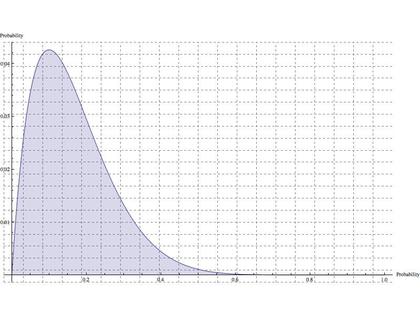
　このグラフを眺めてみると、各戸がバイクを持っている確率としては、「確率が一番高いのは1/10程度だけれども、バイクを持つ確率は、それより実は結構高いのかもね」という具合になっています。そして、バイクを持つ確率が上のグラフのような場合に、さらに「100戸全て入居済みになった時点でのバイク保有数予測」をしてみたのが次(下)のグラフです。

　10戸入居時点でバイクが１台だけだったから、全部で100戸のマンションならトータル１０台のバイク置き場を用意しておけばいいかなと思ったら…わっ！バイク置き場が全然足りない事態になってしまった ！？と冷や汗をかくことになりそうです。

　日常生活の中では、こんな「ご近所さんの間ですったもんだしがちな割り当て数に関する難問題」に出会うことも頻繁にありそうな気がします。…なんていう風に考え出すと、あぁ学校の勉強をもっと真面目にやっておけば良かった…（泣）と思ったりしそう、です。

■水が金網の上で・指に押されて転がる日　

　一週間前の夜、六本木の古民家で、いくつかの「新技術」を体験してきました。そんな新技術の中のひとつが、超撥水性の塗料材料です。疎水基が先端にあるトゲトゲ・イガイガ形状のシリカでコーティングすることで、表面付着力を通常の百分の一近く下げた…という材料です。

　「コップに水を入れて目の細かい金網で蓋をすると、コップを逆さにしても（表面張力のために）水がこぼれない」なんてビックリ実験ネタがありますが、この超撥水性塗料を金網に塗ると、その上に水を優しく載せると、水はスライムのように気持ち良く転がり動くだけで、金網をすり抜け・滴り落ちることもありません。

　周りから力が掛からないければ、水は「丸くちぢまっている」のが自然というわけで、（地球の重力はなくせないにしても）表面付着力を限りなく小さくすると、水は滑らかで何やら丸っこい塊に変身します。その水の塊が見せる不思議な風景と、その水に触れると味わうことができる心地良い感覚は、何だかとても気持ちが良くて…そんな快感をお伝えしたくて、こんな動画を撮影してみました。