hirax.net::inside out::12月16日

■構造欠陥？　

　そういえば、こんなので遊んでみたのだった。ウナギの寝床システムはStructureポイントではとても不利なようである。が、「間口が狭くて奥行が長い」というウナギの寝床システムこそが個人のWEBサイトにはふさわしいと私は思う。だって、「間口が広いけど奥行が短い」てちょっと味気ないしね。（リンク）

■おもしろモーフィングを作ろう　

　ちょっと面白いか。（リンク）

■校正・較正　

　私の感覚では計測器の場合は「較正」。校正だと頭の中で赤ペン先生が登場してしまう。
　で、新明解は、
　校正 = (1)原稿や原資料などとつき合わせて、文字や図版の誤りを正すこと。(2)〔測定器などの誤差を〕基準に照らして正すこと。( (2)のもとの用字は、「較正」 )
　ということで、語源が較正だということで。 from つっちーのよろず日記。

■手持ちマウスに無線式モデル　

　レーザーポインタは（使う人も含めて）大キライな私としては、この手の商品はうれしい限り。発売されたら、もちろん買う。 from hardでloxseな日々（リンク）

■夕日間近の海辺で　

　青と緑の混じりあったような色。とてもキレイ。海を囲む箱庭のような山はちょっと京都の山を連想させる。画面の右上がケラれているのは鏡筒が折れて？いるから。（リンク）

■船の音と波の音　

　波音と船のエンジンの音が合わさって、とても良い感じ。（リンク）

■波音の向こうの大瀬崎。　

　この直後には、波が足もとにいた。とてもゆったりとした景色と時間。（リンク）

■水平線の彼方　

　青と赤が混じりう水平線。新宿のネオンもきれいで憧れたりもするけど、こんな自然の色もとてもきれい。（リンク）

■心地良い波音　

　画面は90度回転しちゃってます。。（リンク）

■感温液晶の入手法　

　感温液晶シートですが、実験材料でなくて遊ぶのに使うのでしたら、
光洋　03-3212-1571
日比谷パークビル9F
平日8:30-5:30
JR有楽町駅近く
にあるようです。また、もっと違った実験用となると、例えば日本カプセルプロダクツTel.03-3863-3076とか専門のところがあります。
　この質問メールはとても多いのでFAQ作成。

■ポリマー磁石　

　無色のポリマー磁石というのは面白い。極低温時だけでなければ、もっと面白い。価格的にも某用途用には無理だろうなぁ。（リンク）

■ギタリスト改め山男　

　昨日、いつものように新宿のICI石井スポーツへ顔を出した。「オレなんか最近もうなんか健康的で、今年なんか夏には山登り三昧だ〜」という元バンド仲間にビックリ。何が彼をそう変えてしまったのだ？　って、仕事先に決まってるか。彼の彼女は山用品コーナー担当だし。

■課外授業 明和電機　

　「役に立たないモノ作り」　ちょっと憧れる。

■ビデオの中の飼い犬　

　三宅島から避難中の家族が飼い犬を仕方なく手放し、違う里親の手元へ。元の飼い主は飼い犬にもう会えないので、里親が撮影したビデオを見つめる。

■新サーバー稼働　

　hirax.netは12/25に新マシンに移行します。その新サーバーが今日から稼働し始めました。作業は少しづつしていこうと思いますが、各ユーザー・各ゲストにはご迷惑をおかけすると思います。また、サーバースペックが大幅に（これまでが貧しかったので…）向上するはずですので、レスポンスもよくなるのではないか、と。

■引っ越し前の大掃除　

　というわけで、引っ越し前の大掃除をしてみました。勤務先はアクセス制限でランクから（というより何処からも）消え、そして、いつものように競合他社が（少なくとも）二社ランクインしているところがなんというかかんというか…。あれ？エプソンも制限がかかっているんでしたっけ＞関係者の方。

■タイトルはいつもPukiWiki　

　新しいサーバーにPukiWikiをインストールしてみようかな、と思った。で、Pukiwiki.orgやreimy.comを眺めた。で、よしやるぞ、と思いながら、何にも知らないワタシはいつものようにGoogleで検索をかけてみた。で、思った。PukiWikiはGoogle殺しかも。というわけで、まだ今日は入れてないのでした。

■武蔵小杉で　

　今日の夕方近くに見た景色。十二月も終わりに近いのに、まるで秋半ばのような午後。

■プリントゴッコで浮世絵年賀状　

　とても面白い「プリントゴッコで年賀状 浮世絵」　from 和の心に酔いしれろ

■early apple　

　昨日、Powerbook G4を譲ってもらったので、ようやくMac OS Xビギナーになった。というわけで、眺める二十年近く前のappleのビデオを眺めたり、appleの情報を眺めたり。　from COULD

■「電子写真技術のシミュレーションに関する講習会」　

　機械学会の情報・知能・精密機器部門主催の「電子写真技術のシミュレーションに関する講習会」が来年の3月22,23日に2日間にわたり開催されます。いつものように良く言えばトリ、悪く言えばグリコのオマケで講演を行います。結構みっちり内容の詰まった感じになっていて、その割に聴講料が会員30,000円（学生員10,000円），会員外40,000円，一般学生20,000円と格安です。教材のみでも会員4,000円，会員外5,000円とこちらも格安ですが、やはり受講した方がお得か、と思われます。特に「やってみてから考えよう」症候群に陥っている人にはお勧め、かも。

■「技術者・研究者のためのすぐに役立つプレゼンテーション技術」　

　というわけで、来年1月21日(金)に開催予定の「技術者・研究者のためのすぐに役立つプレゼンテーション技術」の方も再度宣伝しておきます。

■ハーフトーン・スクリーン　

　45度ラインスクリーンと90度記念写真スクリーン。

■JavaScriptで動くスプレッドシート　

　JavaScriptで動くスプレッドシート。計算まではしなくても、これは確かに面白い。 from TokuLog! -Shibuya.pm で僕と握手-

■武蔵溝ノ口 / 東京　

　「溝ノ口でMathematicaを使うとこんなことができる」という内容の講習の講師をやった。「こんなことも簡単にできて」「あんなことも簡単にできて」Mathematicaってスゴイ、使ってみたい、というような感想を聞く。…しかし、そんなことがあるわけはない。やはり道具は単に道具なんだから。
　スキーで急なコブ斜面を滑るとき、上手い人の後を滑っていると、スムースに簡単に滑ることができたりする。上手い人が選んだ一番良いコース取りを追いかけてみれば、簡単に見えたりする。けれど、さて自分で滑ろうとすると、何が何だかわからなくなるのが普通だ。

■河辺の景色　

■「19世紀の点光源」と「21世紀の面音源の時代」　

　「遊びの博物誌」の中で、障子などに手で影を作りさまざまな形を浮かび上がらせる「影絵」が一般的でなくなったのは、「点光源」が世の中から消えたからではないか、という想像がされていた。火を灯りとして使っていた頃、あるいは、初期の白熱灯を使っていた頃、夜の部屋を照らす光源は点光源に近かった。そのため、その光を手で遮ることで生じる影絵は明瞭な輪郭をともなって浮かび上がっていた。しかし、点光源が私たちの周りから消えると同時に、影絵も姿を消した、というわけである。

　私たちは光と目を通して世界を眺める。それと同じように、音と耳を通して世界を聴く。面光源が出現したことで、柔らかな人工光が私たちを照らすようになったが、音の方はまだそうなってはいない。たとえば、駅のプラットホームや電車の中でスピーカーに近い場所にいたりすると、あまりに音が大きく閉口することが多い。その一方、スピーカーから離れていると、今度は音が聞こえにくくなり、何をアナウンスしているのか聞き取れなくなる。これは、広い面音源でなく、比較的音源が小さい点音源だからである。携帯電話のスピーカーのように「限られた人に聞こえれば良い」という用途であれば、点音源で「聞こえる人・聞こえない人」の間の差が大きい方が良いが、多くの人に等しく・うるさくなく・小さくなく聞こえて欲しい用途となると、点音源のスピーカーでは望ましくないように思われる。

　吉永小百合は、「ブラウン管テレビは20世紀に置いてきた」と言った。それと同じように、私たちは、点光源も19世紀から20世紀の辺りの時代に置いてきた。そう考えると、点音源もそろそろ「置き時」なのかもしれない。かつて点光源を捨てて面光源を得たように、点音源から面音源へ切り替わっていく時代なのかもしれない。

■「ピッチャーが踏み出す両足の間隔」と「人体のプロポーション」　

　野球のピッチャーが投球を行うとき、理想の足を踏み出す幅は「足のサイズを基準にして、およそ６足半の長さ」だという。ピッチングの教科書を見ると、そう書いてある。たとえば、足のサイズが25cmの人であれば、25×6.5=162.5cmほど足を踏み出して、ボールを投げるのが理想的なフォームということになる。

　この数字は「理想的な投球を行うためには、ピッチャーは自分の身長とほぼ同じ長さだけ、足を広げて投球を行わなければならない」ということを意味している。ダ・ヴィンチの人体の素描を思い起こせば、それはつまり、ピッチャーは両足を180°近くも開脚した状態でボールを投げるということだ

　180°近く足を開きながらボールを投げるわけないよなぁ・・・と思いつつ、ピッチャーがボールを投げているようすを見てみると、確かに両足を身長と同じくらい近く開いている。広げた両腕と同じくらいの長さに、両足を広げている。

　野球の練習のために、相撲の「股割り」を長時間続ける練習をするとも聞く。野球のピッチングは調べれば調べるほど面白い。

■エクセルでシミュレーション　Vol.10　二次元非定常熱伝導問題シミュレーション＋P(ID)制御エクセルシートを作ってみよう　

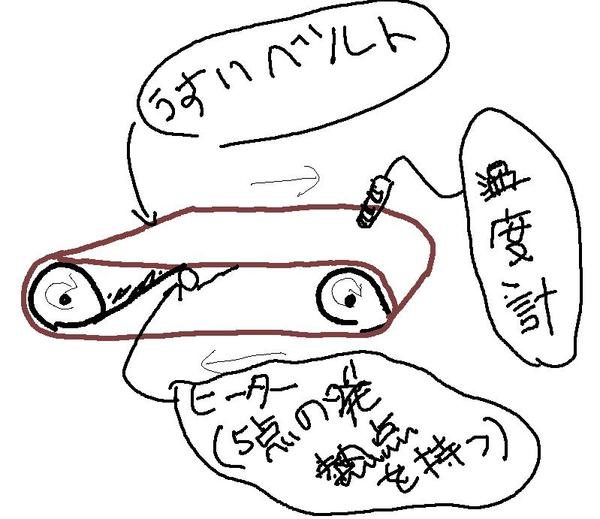　「エクセルでシミュレーション　Vol.9　二次元非定常熱伝導問題の温度変化グラフも作ってみよう」で、二次元非定常熱伝導問題を解くシートを使いながら（実用的範囲では三次元問題と大差がない）、ヒーターで回転するベルトを高温にした場合の、その回転ベルトの温度分布がどのように変化していくかを計算し、グラフ化し、さらにベルト中の一部分の温度を時系列的にモニターする機能を付けた、シートで遊んでみました。

　そこで、今回は、センシングしたベルトの温度を用いて、ヒーターの温度を簡単なPID制御を使ってフィードバック制御するエクセル・シートを作ってみることにしましょう。

PID制御とは、調整量を（現在の）出力値と目標値との差に比例＝Proportionalした量、その（過去からの）積分=Integralに応じた量、および（その瞬間に次にどのように変化するかという）微分=Differentialに応じた量にしたがって変える制御です。言いかえれば、現在（Proportional）・過去（Integral）・未来（Differential）の挙動に応じて、制御調整量を変えてやろうという制御です。比較的、古典的な制御手法ですが、現在でも、もっとも一般的な制御手法です。

　まずは、前回のエクセル・シートでヒーター部分を単純に（計算をさせ始めてから＝回転ベルトに対するヒーターを動かし始めてから）100℃にし続けた場合の計算過程を示してみます。つまり、何の制御もしない場合です。その計算結果が、下の動画です。上の動画で上に示したグラフが、回転ベルトの温度分布を示したグラフです（回転ベルトを切り開いたように温度分布を示しています）。動画中の下の折れ線グラフは（上のコンター図で灰色丸部の温度の時間変化を示したグラフです）。ちなみに、縦軸は0℃から150℃までで、横軸が時間軸です。

　下の折れ線グラフを見れば、上のコンター図で灰色丸で示した部分の、温度が時間に応じて上昇し、やがて100℃近くになっていることがわかります。

　さて、次にPID制御を行ってみることにしましょう。…とはいえ、最初は簡単のために、「灰色丸で示した部分の温度と目標調整温度である100℃との差をヒーターに足す（ネガティブ・日―ドばっく）」という「P=比例成分=現在の違い」だけを利用したP(ID)制御を行ってみます。つまり、現在の出力と目標出力の差異のみをヒーター出力に（適当な比率で）足し合わせてみるのです。言いかえれば、ベルトの温度が0℃なら、ヒーターを200℃くらいにすることで、急激にベルトを温め温度を調整し、目標温度100度と現在のベルト温度の差が小さくなってきたら、ヒーターの温度を110℃くらいに変えてやる・・・というような制御をしてみます。そんなシミュレーション計算を行ってみた結果が、下の計算結果になります。ちなみに、ヒーターの制御温度はエクセルのシートでB32セルで計算されています。また、灰色丸のセンサ取り付け部分（を示した）の温度を示す下の折れ線グラフは、先ほどと同じく、縦軸は0℃から150℃までの温度を示し、横軸が時間軸となっています。

　この結果動画を見るとわかるように、「P=比例成分=現在の違い」だけを利用したP(ID)制御（=積分成分と微分成分を使わない）制御では、ベルトの温度は早く立ち上がりますが、ベルトの温度は振動して、なかなかすぐに安定してくれません。しかも、早く温度を立ち上げようとすると、温度振動は大きくなってしまい、温度振動を防ごうとすると、なかなか温度が早く立ち上がってくれない、という相反する関係になっています。いわば、（ある程度、減衰がある）強いバネと弱いバネの振動と同じような現象が起きてしまいます。

　さて、それでは、一体どうしたら良い制御ができるのでしょうか。・・・せっかく、簡易にエクセルのような（表計算＝スプレッドシート・ソフトウェアを使った）熱伝導方程式を使ったシミュレーション計算を行うことができる環境があるわけですから、今回扱ったPID制御のような古典的な制御をもう少し復習してみようと思います。

　そして、せっかく熱伝導方程式を計算してみたりしているわけですから、そういった微分方程式（つまり現在から未来を示す式）を使うことで実現できる、最適化制御についても考えてみることにします。

■「”１画素・１フレームのみ”からの動き検出!?」のナゾを解く　

　画像中の「動き」のようすを「オプティカルフロー」という言葉で表します。そして、「道路をビデオカメラで撮影し、画像中の（各画素の）動き＝オプティカルフローから、車の速度を検出する」といったような用途に使われたりします。ちなみに、オプティカルフローを表す方程式は、（そのまんまですが）オプティカルフロー偏微分方程式と呼ばれます。

　先日、「画像中の動き＝オプティカルフロー」を「単一フレームのみで知ることができる」という技術展示を見て、ん？と首をかしげました。”動き”というのは、時間を経て画像がどう変化（移動）したかということですから、もしも、時間方向に関する何らかの手がかりがなかったとしたら、「動き」というものは知りようがない情報であるからです。

　今回展示するシステムは、時間相関イメージセンサを用いることで始めて可能になったもので、1画素、1フレームだけでオプティカルフローを検出できます。フレーム間の移動量の制限はありません。アルゴリズムは数学的に厳密な解を少数回の代数計算だけで生成します。

　技術報告パネルに書かれた数式を眺め、動作をイメージしてみて、その疑問を解決する「答」がわかりました。ここで言う「単一フレーム」は、「ある瞬間の画像」を意味する「（いわゆる）フレーム」ではなかったのです。私が首をかしげた技術、「時間相関イメージセンサ（複素正弦波変調撮像）によるオプティカルフロー検出」を（私と同じように）疑問に感じた人もいらっしゃるかもしれませんので、この「単一フレームのヒミツ・トリック」に関するメモを、下に書いておきます。

　まず、時間相関イメージセンサ（複素正弦並変調撮像）は、（たとえば1/30秒毎に映像を出力するのであれば）1/30秒の間ずっと各画素への光量を「三角波を掛け合わせた上で」積分し続けます。そのように三角波を掛け続けつつ積分し続けた結果を、１/３０秒の後に出力します。これが「１フレーム」です（図中の①「式をイメージしてみる」という部分です）。…勘が鋭い人なら、この時点でもうおわかりでしょうが、この技術報告中での「１フレーム」は「時間を止めた”ある瞬間”の画像」ではない、というところがミソであり、「んっ？」と感じる疑問・謎を解くカギです。

　もっと「わかりやすく」するために、三角波を矩形波に変え・１フレーム内の”時々刻々”を”２つ”だけ考えてみることにしましょう。つまり、「本来は１フレーム内で連続的に三角波と画素値を掛け合わせつつ・積分する」という処理を、「１フレーム内の前後２瞬間に矩形波と画素値を掛け合わせて、さらに足す」と単純化してみることにします（図中の②「わかりやすさのために、Sin波を矩形波にしてみる」という部分です）。

　すると、話が単純明快に見えてきます。なぜなら、（たとえば）１フレーム内の前半で矩形波の値がマイナス１・後半がプラス１とすると、「１フレーム内の前後２瞬間に矩形波と画素値を掛け合わせて、さらに足す」ということは、「１フレーム内の後半画像から前半画像を引く」という、まさに異なる時間の映像間で「差分画像」を計算する、という処理になっているからです。…それは、まさに普通にオプティカルフローを求める（よくある）手順そのまま、です。

　というわけで、「時間相関イメージセンサ（複素正弦波変調撮像）によるオプティカルフロー検出」を「わかりやすく」してみました。

　しかし、このカメラの「発想」は意外で面白く感じます。普通のカメラは１フレームの間光を単純に積算し続けていたりするわけですが、このカメラでは単純な積算でなく時間方向に「演算」を行います。他の用途にも色々応用ができそうですね。

■関東平野で富士山が一番綺麗に見える場所!?　

　先日、関東平野のちょうど中央辺りに位置する、埼玉県久喜市に行きました。久喜の辺りから見た富士山は、東京から眺めている時より綺麗に高く見えたのが、少し意外でした。。

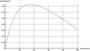
　そこで、「富士山を関東平野から眺める時、富士山からの距離に応じて、丹沢（の山）より富士山がどのくらい高く見えるか？」を調べてみました。富士山と（関東平野から見て富士山の手前に位置する）丹沢の山の高さ関係（仰ぎ角の差分）が、地球の丸さを反映しつつ、どのようになるかを計算してみました。それが下のグラフです。横軸は富士山からの距離（ｋｍ）、縦軸は丹沢の山より富士山が仰ぎ角で何度程度上に見えるかを示しています。また、横軸の最大値は200kmになっていますが、このくらいの距離が「富士山が地平線の下に隠れ・見えなくなってしまう限界距離」です。

　富士山から（というか丹沢に近い箇所から）離れるにしたがって富士山はだんだん高く見え、富士山から１３５ｋｍ程度離れた場所で「富士山が（丹沢より）最も高く見える」状態になります。そして、それ以降は地球の丸さの影響が支配的になり、富士山がだんだん低くなっていくのです。

　つまり、富士を綺麗さに驚いた埼玉 久喜の辺りは、ちょうど一番「富士が（手前の）丹沢山麓よりも高く見える場所」になっていた、というわけです。

　地図を広げて、関東平野上に富士山を中心とする直径135km程度の円弧を書いてみると、（もしかしたら）その辺りは絶品の富士山を眺めることができる場所かもしれません。そんな円弧状のどこかに、空気が澄み渡る冬の空の下で、遠く・高くそびえる富士山を眺めに行ってみるのはいかがでしょうか？

■（ラズパイとMathematicaで）膨大な世界情報が見える「視力矯正メガネ」を作ろう！　

　「ソフトウェアデザイン 2019年1月号」に『（ラズパイとMathematicaで）膨大な世界情報が見える「視力矯正メガネ」を作ろう！』を書きました。

　見上げた空に浮かぶ雲を動かす風、空を飛ぶ電波、街を包む犯罪オーラ…そんなものを景色に重ねて眺めたいと思ったことがある人なら面白いかも、と思います。

　すでに行っていた実験結果やコードをもとに、羽田・クアラルンプール・シンガポール・ジャカルタ…という移動中に書いたので、「世界の色々なものを、色々な世界のその場所で、見えないものを眺めるメガネが欲しい」という思いが少し入っている気がします。