hirax.net::inside out::2008年11月

■パラメトリック・スピーカー・実験キット　

　(下の動画のような)「パラメトリック・スピーカー・実験キット」が秋月電子で1万1800円で発売されている。5×10=50個の超音波発振子を並べ、超音波を干渉させることで指向性の極めて高い出力を可能にするスピーカーキットだ。「どういうことに使うことができるか」を考えてみるのも楽しそうだけれど、何より超音波発振子が並べられたその外観に電子工作ゴコロがくすぐられてしまう。

　特に、右上のパラメトリック・スピーカー・実験キットを使って作られたパラメトリック・メガホンが、極めつけに楽しそうだ。雑踏の中にいる人たちの中の、その中の一人だけにしゃべりかけることができる超面白グッズを作ってみたくなる。あるいは、川向こうにいる人だけに、こっそり話しかけてみたくなる。

■「雑誌DE流行マップ Lite」と月刊「理系ファッション」　

　「雑誌DE流行マップ Lite」をメンテナンスしました。Javascriptコントローラが度データ遅延・動的読み込み・各種表示を行う「雑誌DE流行マップ Pro」のような解析機能は持っていませんが、「あぁ、こんなものが流行っているんだなぁ。こんな付録に惹かれる時代なんだな、そして、こんな人が流行っているんだな」と、時折時代の流れを眺めてみるには良いかもしれません。

　自分の作ったページ群を眺めているうちに、制御回路を上手く動かすことも難しいけれど、ファッションよりは簡単かもしれないなぁ、とふと感じてしまいました。まず、ファッション用語のボキャブラリが足りないように思います。つらつら眺めてみたら、いつの間にか詳しくなったりするのでしょうか。

　月刊「理系ファッション」という雑誌でもあれば、定期購読するのに…(その必要すらないかもしれませんが)。

■hirax.net::mobileと「後で読む」　

　携帯電話からhirax.netを眺めることができるように、Railsの携帯電話用コントローラ(アクション)を書きました。アクセスURLは http://www.hirax.net/mobile/latest です。右上のQRコードがそのURLになっています。ちなみに、 上記URLからは、（結局は、「自分で作った道具」で「自分が作るもの」と「クラス分け」やコトバを集めた"Logo"クラスで書いたように、全部Contentクラスの継承クラスだ（という作りにした） というだけの理由なのですが） "insideout""Tech-logs""Logos""できるかな?"のすべてが同じように扱われます。

　画像などは送出しないようになっていますから、今ひとつ内容は伝わりにくいとは思います。そういうわけで、説明図が必要になるような内容は飛ばし読みし、つまりは、電車中でのお暇つぶしに、雑文が役に立てば幸いです。

　また、PCで「後で読む」用に、携帯電話用ページに(はてな)ブックマーク用のアイコンを設置しました。その際に登録されるURLはPC用のURLです。つまり、同じ記事に対するURLではあっても携帯電話で（その時）アクセスしているURLではありません。あくまで、後で画像付き・レイアウト付きで(つまりはPCで)読み直すためのブックマークだという判断です。

■ダイアモンドの中心にピッチャーマウンドがあるか？　

　「野球」のホーム・ファースト・セカンド・サードベースで囲まれる領域は「ダイアモンド」と呼ばれる。今日の疑問は、「ピッチャーがボールを投げる時に踏む、ピッチャーマウンドにある”プレート”はダイアモンドの一体どこに位置するのか」ということだ。最近、ピッチングにはまっているせいで、そんな疑問にはまっている。

　「自然は対称を好む」という言葉が野球のルールにも当てはまるとしたら、ピッチャープレートはホームベースとセカンドベースの中心、そして、ファーストベースとセカンドベースの中心に位置するのが「自然」に思える。実際のところ、どうなのだろうか。

　四角形のダイアモンドの大きさは、各辺の長さが90'(27.431m)である。ダイアモンドは、ファースト・セカンド・サードベースの中心、そして、ホームベースのキャッチャー側端を結んだ正方形である（ほかのベースと違って、ホームベースはダイアモンドの角に接するように設置された五角形であるために、"キャッチャー側端"ということになる’のだろう）。一体、ピッチャー・プレートはこのダイアモンドのどこに位置するのだろうか。

　野球規則に挙げられている数字、ホームベース端からセカンドベースの中央まで38.795m、ホームベース端からピッチャープレート(15.2cm長)のホームベース寄りの位置までが18.44mという数字、を見ると、ピッチャープレートは、ダイアモンド中央よりホームベース寄りに見える。

　確かに、ヤンキースタジアムを航空写真で拡大して眺めてみると、そういった「ダイアモンド中央よりホームベース寄り」の位置にピッチャープレートがあるようにも見えるような気もする。一体、「野球は対称を好む」のかそれとも、違うものを好むのか、野球の「ピッチャーマウンド」は「ダイアモンド」のどこにあるのか、ダイアモンドの中心でピッチャーは愛を叫ぶのか（古い）、それが(今日の)疑問なのである。

■昔の野球は、バッターに今よりずっと近い位置にピッチャーがいた　

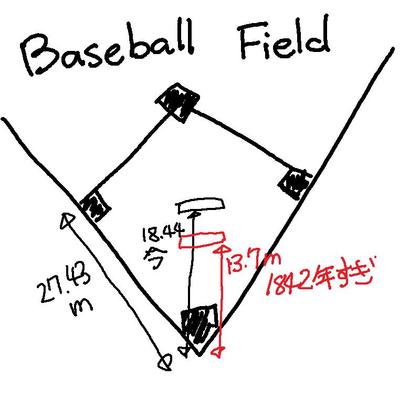　(「ダイアモンドの中心にピッチャーマウンドがあるか？」の続きです)「野球」のルーツには色々な意見がるが、現在の野球ルールの大部分は、1842年頃にニューヨーク市内の紳士クラブが作った「ニューボッカーズ・ベースボール・クラブ」という社交クラブから始まった、と言われている・・・という。「ニューボッカーズ・ベースボール・クラブは、各ベース間の距離を決めた。それが90フィート(27.431m)である。それは、今の野球規則で定められている距離と同じだから、つまり、野球場の「ダイアモンド」は一世紀半以上大きさが変わっていない、ということになる。

　しかし、ホームベースとピッチャー・プレートの距離は違う・・・らしい。書籍を調べていくと、「ニューボッカーズ・ベースボール・クラブ」が作ったルールでは、その距離は45フィート(13.7m)だったという。つまり、今より5m近く短いのである。ということは、ピッチャーは「ダイアモンド」の中心より遙かにバッターに近い位置で愛を叫んでいた、ということになる。

　それから数十年後の1881年に、ホームベースとピッチャー・プレートの距離は50フィート(15.24m)に変わり、そして、それからすぐの1893年に18.44mという現在と同じ距離に変更されたのである。ここで、ようやく「野球場のダイアモンドの中心近く」がピッチャーの位置となったのである。

　まだまだ、キャッチボール（というよりピッチング）にしかはまっていないのだけれど、ピッチングのテキストを読みあさったり、野球経験者にアドバイスを受けていると、野球の沼の奥の深さにはまりまくる今日この頃だ。

■いろんな形・いびつな形の野球場　

　「ダイアモンドの中心にピッチャーマウンドがあるか？」「昔の野球は、バッターに今よりずっと近い位置にピッチャーがいた」で気になったので、試しに近くの野球場に実際に行ってみた。そして、一塁から三塁方向を眺めてみると、やはり、一塁と三塁を結ぶ直線より、ピッチャープレートは、ホームベースよりに位置していた。

　ところで、ダイアモンドの大きさ、つまりは、内野の大きさ・位置関係などは野球規則で決まっているけれど、外野については「フェンスなどはホームベースの端から250フィート(76.199メートル）以上離れていること」という程度の決まりしかない、という。だから、いろんな大きさの、そしていろんな形の野球場がある。右上のピッツバーグ・パイレーツのホームグラウンドの変遷を眺めてみると、1909-1970年までのForbes Fieldも、2001年以降使われているPNC Parkも左右非対称だ。Forbes Fieldは、左右非対称どころか、実にいびつな形をしていて、見ていて楽しくなる。

　こういう野球場のいびつな形は、そのチームの特徴を生んで・あるいはチームの特徴に沿っている、と聞く。それが、また面白い。

　たとえば、守備面から見てみれば、Forbes Fieldは中堅手（センター）が強肩である必要があるだろうし、PNC Parkは左翼手（レフト）が強肩である必要がある。もちろん、攻撃面から見ても、それぞれの球場に応じて、有利なチーム構成がある、ということになる。

　左右非対称なホームグラウンドを持つ野球チームの、野球場の形状とそのチーム構成（特徴）を眺めてみたい。いろんな形・いびつな形の野球場の個性と、そのホームチームの個性を見てみたい。

■斜め下45度から眺める「フェルメール展」　

　東京都美術館で「フェルメール展 光の天才画家とデルフトの巨匠たち」が今夏から、12月14日まで開催されている。フェルメール展に行った時にこんなことを考えた。

　（展示されている）フェルメールの絵を普通に眺めていると、絵そのもののせいか、あるいは、照明との位置関係のせいか、まるで、綺麗な画集を眺めているような気がする。それを逆に言ってしまえば、画集を眺めているのと変わりない、写真撮影した等身大の絵を眺めているのと変わりない・・・ということになってしまう。

　けれど、絵の周囲を覆う手すりくらいの高さにかがみ、絵を少しづつ違う方向から眺めてみると、照明を反射し光る表面を通じて、絵の表面の凹凸が見えてくる。絵の中のどんな色の部分が出っ張っていて、どんな部分が凹んでいるのかが見えてくる。

　つまり、絵がどのように描かれているか・フェルメールがどのように絵を描いていたのかが、朧気ながら見えてくる。灰色・人肌じみた色でキャンパス全体が塗られ、その上に薄めの色と淡い黒が塗られ、その上にさらに荒い黒と白が描かれているような感じが見えてくる。下地やモデリングやグレージング、そして、その上に画家が描いたハイライトと濃い黒い領域が見えてくる。

　「絵が描かれた手順・方法」に興味を持つタイプの人は、レゾネと違う絵を見てみたい人は、フェルメール展を斜め下45度から眺めると面白いと思う。正面から見ると同じ黒が違う黒に見えてきたりと、少し違う立体的な絵が見えてきて面白いと思う。そして、立体的な景色から、その絵が描かれた時の空気が流れてくるように感じると思う。

■ケータイ用 hirax.net 機能追加　

　先日、携帯電話からhirax.netを眺めることができるようにしましたが（トップページ URL は http://www.hirax.net/mobile/latest で右上のQRコードがそのURLです）、関連記事表示やタグを含む記事の一覧表示といった機能を追加しました。ｹｰﾀｲから使う・読む分にはひとまず使いものになる・・・と良いなと思っています。

　あとは、リンク先のケータイ対応化処理や、縮小画像表示機能、あるいは、他マルチメディア機能の記事プレビュー機能でも作ってみたいですね。

■最近のThinkpad（の加速度センサ）に対応した万華鏡ソフト　

Thinkpadで動く万華鏡ソフト、Thinkpadを傾けるとそれに応じて色とりどり綺麗な模様が見える万華鏡ソフトのアップデート版を作って、ここ(kaleidoscopes20081108.lzh 1.4MB)に置きました。最近のThinkpadでも動くようにしています。このソフトウェアを動作させると、下に貼り付けた動画のように画面に万華鏡の中野景色が映し出されます。こういう模様の動きには、何だか不思議なくらい見とれてしまいますね。

■"What Happens in Vegas"　

　少し前、"What Happens In Vegas"(「ベガスの恋に勝つルール」)を観ました。決してA級の映画ではなく、それほど時間が経たないうちにタイトルを忘れられてしまうB級映画なのかもしれません、・・・けれど、面白い映画でした。ひとことでストーリーを表現してしまうと、主人公（キャメロン・ディアス演ずる）ジョイとジャックを中心に繰り広げられるラブコメディ、というものになってしまうのでしょう。しかし、同時に、何かふと考えさせられる、そして、そこで感じたこと・楽しんだことが湯冷めしないままに記憶（けれど、記憶の底）に残るような映画でした。

Ultimately, Jack and Joy discover and identify each other's admirable and loving traits. ・・・ Using a gambling metaphor, Jack tells Joy, "You bet on me and you made me want to bet on myself."
(from here.)

　ジャックが、スロット・マシーンでジャック・ポット、それはまさにジャックの場所です、を当てたことから始まるストーリーは、（些細だけれどもとても的確な異性間の違い・他者への過剰な意識と自分の可能性を信じることができないといったこと・他者と自分の間で自分が自然に立つことができる場所といったものを、スクリーンに自然に浮かび上がらせるように思います。“What happens in Vegas, stays in Vegas”　そんなラス・ベガスのキャッチフレーズとは違い、ラス・ベガスでの出来事がラス・ベガスでで終わらずに、その後も続くのです。

　エンターテイメントとして誇張されて描かれてはいたとしても、スクリーンに映し出されている男女の姿、現代の等身大の男性と女性の姿そのままだと思ったのです。

"I'm really interested in stories about finding love or getting to know someone through dysfunction or adversity," says screenwriter Dana Fox. "I first came up with this story about two people who strangely get to know each other while divorcing. Around that time, I kept hearing the phrase 'What happens in Vegas, stays in Vegas' and thought, if it wasn't already taken, it would make a great title for a film.
(from here.)

■ケータイ版「雑誌DE流行マップ」　

ファッション雑誌を適当につらつら読んで、世間の流行＝ファッションなどを少し眺めてみよう、という「雑誌DE流行マップ Lite」のケータイ版を仕立ててみました。URL は http://www.hirax.net/fashions/mobile/titles.html （右のQRコード）です。

　小悪魔 ageha の最新号の紹介文なんかを読んでみると、

　みんなの兄弟姉妹ってどんな人！？ー新事実発見・age嬢の53％がおねーちゃんだった！！

　あるいは、「好奇心(モバイル用リンク)」なんていう言葉が載っているのはどんな雑誌・・・？という風に好奇心を持って眺めてみるのも面白いかもしれません。「流行」から遠い人ほど、「流行」を知らない人ほど興味深く感じられるのかもしれない、と思ったりするのです。

■「ボールレンズ」のネックレス　

　たとえば、凸レンズの形を描いてみると、その形が球形のガラス玉とよく似ている形であることがわかります。つまりは、ガラス玉は一種の凸レンズです。球形の形をしたプラスチックやガラスは、ボールレンズという名前のレンズであるわけです。曲率が極めて高い凸レンズなのです。

　ボールの直径に応じて拡大率が大きくなるので、大きなボールレンズを使えば、大きくものを拡大することができます。・・・といっても、もっとも、球面収差がとても大きいので、周辺部はボケてしまいます。

　ちなみに、屈折率が2.0のもので作ったボールレンズが球面収差が一番小さくなります。ランタン系ガラス材料のS-LAH79は屈折率が2.003と2.0にとても近いので、球面収差が小さなボールレンズを作ることができます。

　ところで、光学カタログを眺めていると、サファイヤやルビーで作られたボールレンズも載っています。サファイヤ/ルビーは屈折率は1.8弱なので、球面収差は小さくないのですが、その硬さからキズがつきにくいということで、商品化（つまりはよく使われている）されているのです。

　サファイアで作ったボールレンズも、ルビーで作ったボールレンズあっても、どちらも直径1cm程度で七千円くらいです。拡大鏡・マイクロスコープを持ち歩く人も多いと思いますが、サファイア・ルビーで作ったボールレンズを持ち歩いてみるのはいかがでしょうか。透明なサファイアで作った「ボールレンズ」をネックレスにしてみたら・・・あるいは指輪にしてみたら・・・お洒落な光学技術者になれるかも？・・・それとも、単に変な光学技術者になってしまうかも？

■シャーロック・ホームズにもわからない「青い紅玉」のナゾ　

　（「ボールレンズ」のネックレスの続きです）ルビーもサファイヤも、酸化アルミニウム（Al2O3）の結晶「コランダム」です。結晶中にクロムが混じると赤色のルビーになったり、鉄やチタンが混じると青色のサファイア（赤色以外のコランダムをサファイヤと呼びます）となったりします。

　サファイヤとルビーという言葉を聞くと、コナン・ドイルの「青い紅石」""THE ADVENTURE OF THE BLUE CARBUNCLE""を思い出す人も多いと思います。知らない人は青い？紅石？と思うかもしれませんが、「青い紅石」というのはシャーロック・ホームズが主人公のミステリの題名（の一番有名な邦訳の一つ）です。

　コナン・ドイルが「青い紅石」"THE ADVENTURE OF THE BLUE CARBUNCLE"を書いた当時、「カーバンクル」"CARBUNCLE"は「丸く磨いた赤い宝石」を指す言葉でした。それと同時に、その当時はまさに青いコランダム、つまりサファイヤが各地で産出され、広まり始めた時代でもありました。とはいえ、その科学的な定義や名前などはまだ定まっていない時代でもあります。

　ですから、シャーロック・ホームズが「青い紅石」で扱った宝石は、「本来は赤色であるはずなのに、青く輝く珍しい貴重な宝石」であるのかもしれませんし、あるいは、現在と完全に同じ意味での「青いサファイヤ」なのかもしれません。

　万物に通じていて・信じられないほどの推理力を発揮するシャーロック・ホームズでも、その「青い紅玉」"BLUE CARBUNCLE"が何なのかは、きっとわからない時代だったことでしょう。そう思うと、「青い紅玉」が何なのかというナゾに、とても興味を惹かれてしまいそうです。・・・というわけで、「青いガーネットの秘密―“シャーロック・ホームズ”で語られなかった未知の宝石の正体」を読んでみようと思います。

■「色が変わるガーネット」と"Spectrum Color Conversion"　

　深紅のルビーや青や緑のサファイヤ、つまりは宝石「コランダム」を眺めていると、宝石「ガーネット」に目を惹かれました。コランダムにも色々な色のものがあるのと同じように、ガーネットにもさまざまな色を呈するものがあります。そんな中で、目を惹かれたのは”色が変わる”カラーチェンジガーネットです。

　陽の光の下や白熱灯の下で、あるいは、蛍光灯の下で・・・つまり、その時々の照明光・環境光に応じて違う色姿を見せる「カラーチェンジガーネット」は実に魅力的に見えます。

　ガーネットを照らす光の波長強度分布の関係と、ガーネットの光吸収率分布と、さらにそのガーネットを見る人の色覚・色認識の機構が掛け合わされることで、カラーチェンジガーネットはその色を状況に応じて変えるのでしょうか。そして、その色の変わり具合が激しいのがカラーチェンジガーネットなのでしょうか。

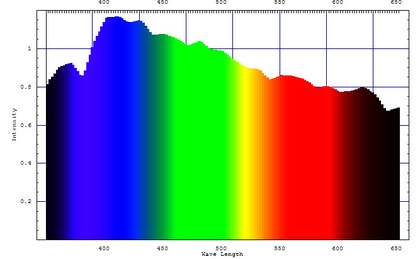　そういえば、以前光スペクトルデータ操作用のMathematicaライブラリを作ってみたり、そのWEBアプリケーション版のSpectrum Color Conversionを動かしてみました。こんなカラーチェンジガーネットを見ると、その色がどのようなもので・どのように感じているのかを、自分の指でMathematicaのコードで書き下ろしてみたくなります。そして、その「色」の仕組みを頭の中でも納得してみたくなります。

　・・・と思いを巡らせているうちに、ふとそんな色を楽器でコードで奏でたら、指で弦をつまびいてみたら、それは一体どんな音になるのだろうか・・・とふと思ったりもしました。

■「多体問題」と「政治」　

　社会学者の橋爪大三郎の言葉としてこんな一節を聞いたことがある。

二人の人間の関係は「力関係」だが、
三人以上の人間関係は「政治」だ。

　その時、妙に納得した理由の一つに「多体問題」が頭に浮かんだことがある。「相互に影響を与えあうものの挙動を扱う問題」を連想し、２つのものの間の問題、つまり「二体問題」は解くことができるが、三体以上になると（極めて少ない例外を除けば）一般的に解くことができなくなる。

　ここで、振り返って橋爪大三郎の言葉を読み直してみると、それはこんな風に変わる。

二人の人間の関係は「力関係」だが、
（それは力関係で厳密に決まる）
三人以上の人間関係は「政治」だ。
（それがどのように動いていくかはわからない）

　この言葉を聞いてから、「政治」の話を聞くたびに、頭の中でその多体問題を図示してみたくなった。そして、どんな相互作用が働いて・どんな関係にある多体問題なのかを描いて眺めてみたいと感じるようになった。

　たとえば、今のさまざまな政治問題を図示して見ると、一体どのような図になるのだろう。どんな眺めになるのだろうか。

■「色を変える"宝石"ガーネット」と「"変化"するMathematica」　

　「色を変える"宝石"ガーネット」の光吸収スペクトルを探すうちに、こんなページやこういったページに出会いました。こういうページを眺めていると、単純な色名では表現できない宝石の光吸収スペクトルを(数式処理プログラムの)Mathematicaで関数にして、さまざまな照明の中で、宝石が外に見せる色を計算するライブラリを作りたい、と思ったりします。

　光吸収スペクトルは変わらなくても、照明光スペクトルや視覚スペクトルに依存して「見た感じ」が変わるようすをMathematicaで描いてみたいと思ったわけです。

　そんなことを思いながら、もうすぐ公開される Mathematica の新バージョン、バージョン7を見ました。そのMathematicaが"変化"し続けるさまは、なぜか「色を変える"宝石"ガーネット」を連想させました。さまざまな機能が追加され、姿・見た目が大きく変わっているように見えても、少しその新たな装いを脱がしてみると、その下にはこれまで同じ「HEADで表現される構造が組み合わさったオブジェクト」が見えてきて、そこに色を変える宝石と同じさまを感じたのです。

　色鮮やかに映える機能をとても魅力的に感じる人は、多いことでしょう。その一方で、特に変化するわけでもない内部の光吸収スペクトルや基本オブジェクト構造に不思議に心惹かれる人もいるように思います。「さまざまな機能を使って何かをしたい」と思う人もいれば、「基本構造を組み合わせて何かを作ってみたい」と思う人もいそうな気がします。

　もちろん、その時の気分で「どっちが好き」かは変わることも多いかもしれません。このページを読む人は技術系の人が多いと思いますが、（この瞬間の）あなたなら「どちら」を好むのでしょう。どちらを選ぶのでしょうか？

■Ruby版 Win32GuiTest クラスを作りました。　

　（この記事の続きが「続：Ruby版 Win32GuiTest クラスを作りました。」）になります。

　Ruby版 Win32GuiTest クラスを作りました。PerlのPerlのWin32-GuiTestと同じような機能を集めたものです。つまり、MoonWolf　さんのWin32::GuiTestと同じようなものです。

　夕方からPerlのWin32::GuiTestの関数リストを見て、それと同じようなものををつらつら書いていき、私自身が使いそうにない関数・機能が続き始めた辺りでやる気が下がってきたので、とりあえずソースコード(guiTest.rb)をここに置いておくことにします。

　(コードにも入っていますが)サンプルコードは下記のようになります。これは、「ワードパッドを立ち上げて、ウィンドーを全面に持ってきて、適当に文字を入力して、その文字をコピーして数回ペーストした後に、保存せずに終了する」という具合に動きます（'RichEdit20W'の部分は、クラス名からの子ウィンドゥ検索を示すために入れたので、実際にはなくても構わない部分だと思います）。

  gui=Win32GuiTest.new
  gui.run('wordpad.exe')
  sleep 2
  gui.setForegroundWindow(
    gui.findWindowLikeName('ワードパッド').first[0] )
  gui.setFocus( 
    gui.findWindowLikeClass('RichEdit20W').first[0] )
  gui.sendKeys('This is a sample.{ENTER}',1)
  gui.sendKeys('^a^c')
  5.times do |i|
     gui.sendKeys("#{i} ...{ENTER}")    
     gui.sendKeys('^v')    
  end
  gui.sendKeys('%f',2)    
  gui.sendKeys('x',1)    
  gui.sendKeys('n',1)

■続：Ruby版 Win32GuiTest クラスを作りました。　

　（この記事は「Ruby版 Win32GuiTest クラスを作りました。」）の続きです。

　 Ruby版 Win32GuiTest に関数・機能を追加しました。下の動画は「ペイントを立ち上げて、ウィンドウの場所を動かし、絵を描いた上で、ビットマップファイルを保存する」という作業をRuby版 Win32GuiTestを使ってRubyで自動で行ったものになります。

　実際のコードはソースコード(guiTest.rb)に入っているように、下記のようになります。次はリサージュ図形でも書いてみることにしましょうか。

  gui=Win32GuiTest.new
  gui.run('mspaint.exe')
  sleep 1
  w=gui.findWindowLikeName('ペイント').first[0]
  gui.setForegroundWindow(w)
  gui.moveWindow(w)
  r=gui.getWindowRect(gui.getForegroundWindow)
  sleep 1
  360.times do |i|
    rad=i*2*3.14/360.0
    x=r[0]+200+100*Math.cos(rad)
    y=r[1]+200+100*Math.sin(rad)
    gui.mouseMoveAbsPix(x.to_i,y.to_i)
    gui.sendLButtonDown if i==0
  end  
  gui.sendLButtonUp
  gui.sendKeys('%f',2)    
  gui.sendKeys('x',1)    
  gui.sendKeys('y',1)    
  gui.sendKeys('TestBitmap.bmp',2)    
  gui.sendKeys('{ENTER}',2)    

■ペイント automated by Ruby Win32::GuiTest　

　というわけで、リサージュ図形(もどき)を「ペイント automated by Ruby Win32::GuiTest」で描いてみました。ペイントソフトでリサージュを（マウスを使って）描くのは大変ですけど、自動化すれば簡単ですよね。・・・簡単・・・ですよね・・・？

■0.2×11-2 = …？のヒミツ　

　前に何度も見たことでも、久々に見たり読んだりした時、新鮮に面白く感じることは多いように思います。

　Mathematicaのデモ中で、「計算の丸め誤差」をエクセルで見ました。数値計算の有効桁数や丸め誤差を気にする人は多いでしょうし、エクセルや多くの計算プログラムやあるいは言語で「誤差がどんどん重畳されていくようす」を眺めたことがある人も多いと思います。いえ、実際のところ、技術系の人であれば、そんなデモを眺めたことがない人の方が稀少ではないでしょうか。とはいえ、前に何度も見たことでも、やはり新鮮に面白く感じることは多いように思うのです。

　そこで、(Mathematica のデモンストレーション中で演じられていた)エクセルで「0.2×11-2」の計算を繰り返していったときのようすを動画として再現して貼り付けてみました。

　まず、エクセルで、0.2×11-2を計算します。そして、『「(0.2と表示された)その答え」×11-2』と計算するのです。そして、その答えにさらに…と計算を繰り返していくわけです。

　すると、あっという間に丸め誤差が積み上がっていって、20回も計算を繰りかえすと値が1000くらいになってしまいます。こういったことは、浮動小数点の精度を考えれば当たり前な話です。しかし、「タネがわかっていても面白い手品」があるように、こんなデモンストレーションも（たまに眺める分には）見ていてとても楽しく感じてしまいます。

　もしかしたら、特にこの手のデモを楽しく感じるのは、「キカイが動いている仕組み・仕掛け」を感じることができるからかもしれません。アレ？と感じ、その興味を入り口として、目の前の現象を眺めていくうちに「キカイが動いている仕組み・仕掛け」が見えてくるからかもしれません。

　そして、いつも「それってとても楽しいと思わない？」と感じるのです。

■ペプシコーラ NEX の食玩で「イルミネーション・ライト」を作ってみる　

　一時期、まるで、どのペットボトル・ジュースにも食玩が着いているように感じました。たとえば、ペプシコーラには、右の写真のような小さなロボットアクセサリがオマケとして着いてきていた時期がありました。

　ペットボトルに小さな可愛いロボットが入っていて、捨ててしまうには名残惜しい感じでした。そんなこんなで、ずっと色とりどりのロボットたちが机の上に並んでいたわけです。

　ふと、赤く光る発光ダイオードをその小さなペットボトルの中に入れてみました。そして、点滅させてカラフルなロボットたちを照らし出してみたのです。それが下の動画です。名付けて、コカコーラ・ライトならぬ、「ペプシコーラ NEX・ライト」です。20色のロボットが光るイルミネーション・ライトです。

■Rubyで「シリアル通信スレッドクラス」を作る　

　Rubyで「(Ｒｕｂｙシリアル通信ライブラリ（Windows用）TEXCELL を使った)シリアル通信スレッドクラス」を作りました。ソースコードとサンプルはここに置いておきます。”Microsoft Windows VISTAではほとんど見捨てられているような”シリアルポートでの送受信をRubyでスレッドを使って行うクラスです。Queueにデータを突っ込めば「シリアル通信スレッドクラス」から自動的に送信されます。また、受信した文字列が「（指定した改行コードで）一行になるたびに」receiveイベントが呼ばれるので(また、その際にQueueを指定しておけば受信行が自動的にそのQueueに追加されていきます)、読み込みのタイミング・必要な情報がまだ途中までしか読み込まれていない場合などの処理を気にすることなく使いたい、と考えながら作ってみた「シリアル通信スレッドクラス」です。
　たとえば、COM3で受信した内容をコンソールに出力するだけであれば、このようなコードで動くはずです。

require 'comThread'
receiveComThread=ComThread.new({:icomno=>3})
receiveComThread.start({:receive=>true, 
　　　　　　　　:receiveMonitor=>true})
sleep 60
receiveComThread.stop

  require 'comThread'
  q=Queue.new
  receiveComThread=ComThread.new({:icomno=>3,:rq=>q})
  sendComThread=ComThread.new({:icomno=>4,:sq=>q})
  receiveComThread.start({:receive=>true,
　　　 :receiveMonitor=>true})
  sendComThread.start({:send=>true})  
  sleep 60
  sendComThread.stop
  receiveComThread.stop

　以前、こんなことを書きました。

　「計測・解析ソフトウェア/ハードウェアのハック」が実験系技術者の一番のLifeHackかもしれない…と思っています。その思いを逆に言うならば、実験系技術者が費やす多くの時間を、計測・解析処理が消費していると思っているからです。そして、一番時間を消費している部分の高速化をすることが、全体の高速化に効果的だろう、と思っているわけです。

　そんなこんなで、何を今更…という、Perlで「シリアル通信とユーザインターフェース自動制御」のやり方を整理しておくことにしました。なぜかというと、経験的に(既成機器をを使わざるえないことが多い)「計測・解析ソフトウェア/ハードウェアのハック」は、シリアル通信制御とユーザインターフェース自動制御でほとんどの場合対応できる、からです。

■DSサイズの水彩画セット　

　文房具屋で「DSサイズの水彩画セット」を見つけ、思わず買ってしまった。実際には、任天堂のDSよりもっと小さくて、ずっと昔に流行った「ゲームウォッチ」とほぼ同じサイズの、筆記用具入れの中に、さらにケースごと入ってしまうほどに小さな「水彩画セット」だ。

　初めてカメラを手にした時には、誰もが景色をとても新鮮に眺めるようになる。目の前にある小さなもの一つ一つに興味を感じてしまうように思う。

　それと同じように、・・・もしかしたら、それ以上に「お絵かきセット」を手にすると、目の前の景色をとても新鮮に眺めるようになる気がする。目の前を通り過ぎていく人、振り返った時に見える街、前にある道・・・そんな色んなものがとても不思議に見えてくる。どういう風に世界が見えているのか、どういう風に筆を動かせば、一体全体、その世界を手元に再現することができるのだろうか、と不思議な気持ちにおそわれる。

　と、頭で考えるだけでは答えが出てこないので、とりあえずいつも持ち歩いて、目の前のものを描いてみることにする。

■Googleで(((0.2 * 11) - 2) * 11) - 2...　

　Excelで計算した「0.2×11-2 = …？のヒミツ」と同じことを、Googleで(((((((0.2*11-2)*11-2)*11-2)*11-2)*11-2)*11-2)*11-2)*11-2を計算（検索）してみるとどうなるでしょうか。・・・やっぱりそれは同じ結果になります。この計算結果を眺めてみれば、色んな「仕組み・仕掛け」が、かいま見えてきます・・・よね。

　やっぱり、それってとても楽しいと思いませんか？

■「ニューシネマパラダイス完全版」と女と男　

　20年前に作られた映画「ニューシネマパラダイス」を、何度目になるのかわからないけれど見ました。見たのは、劇場版でした。エンディング近くでは、完全版で描かれた風景を思い浮かべながら、これも何度目かわからないくらいに泣いてしまいました。

　この映画は本当に男性泣かせの映画だと思っています。どうして、男性泣かせだと感じるかというと、女性にはきっと「当たり前」のことが（特に完全版では）描かれていて、そんな当たり前のことが、私たち男にはわかりづらいからなのかもしれない、と想像しています。だから、その当たり前のことに泣くのかもしれない、とふと思います。

　この映画は手に入れた者の映画ではない。手に入れることができなかった人間の映画だ。

　しかし大多数の人間は何かを失って生きてきた。むしろその離別や喪失の後にその場所に固執せずに、いかに歩みを進めることができるかが、人の成長ではないか。この映画はそれを淡々とつづっているような気がする。

　from ニュー・シネマ・パラダイス 完全オリジナル版 スペシャル・エディション [DVD]

　エンディングシーン、エンディングロール、そして、 その間にはさまれる"FINE"の文字は、劇場公開版と完全版では、ずいぶんと違う印象になります。エンディングシーン、エンディングロール、その間の"FINE"の文字、そのどれも強く否定のしようのないものに変わります。

　もしも、20年前に映画館でニューシネマパラダイスを見た人がいたら、20年の時を経て、またもう一つ別の物語を完全版で見ると・・・また違うものが見えてくることと思います。ラストシーンでスクリーンに映し出されるフィルムと、そのフィルムを見る主人公の表情を見ながら、そんなことを考えたりします。

■「探偵ナイトスクープ」と「地表の重力」と「電子天秤の体重計」　

　「探偵ナイトスクープ」を観ていると、北緯45度25分に位置する稚内と北緯25度20分に位置する那覇では(もしかしたらこの数字は「度・分」ではなくて、単に「度」だったかもしれない)、地球の自転の遠心力のために、重力加速度がそれぞれ9.8062273m/s^2と9.7909942m/s^2と、0.155341%ほど違っている。だから、40キログラムの人が稚内から那覇に行くと62.136グラム軽くなる・・・という小ネタを扱っていた。体重40キログラムのマネキン人形を稚内から那覇へ移動させ、電子天秤でその体重を計り、マネキン人形の体重が軽くなるさまを見せていた。

　実際には、緯度によるの違いを生む過程はそう単純でないと思いながらも（参照）、画面を観ていて何より面白かったのが、撮影に使われていた電子天秤だ。40kgを1g未満の誤差で計っていて、つまり、6桁近くの精度を持っているのである。

　その桁数をたとえるなら、「1.6トンの車に、おちょこでお酒を1盃と少しかけた時の重量の違い」がわかるくらい、といことになる。・・・そんな体重計があったら、とても小さな体重の増減に、つまりはとても小さなことに一喜一憂してしまって大変そうだ。体重計に限っては、有効桁数が大きいことが必ずしも良いとは限らないのかもしれない。

■続 「探偵ナイトスクープ」と「地表の重力」と「電子天秤の体重計」　

　（「探偵ナイトスクープ」と「地表の重力」と「電子天秤の体重計」の続きです）探偵ナイトスクープで「稚内と那覇で（マネキン人形の）体重を計る」回で、電子天秤は地域ごとに校正されているという話をしていた。1キログラムの質量の分銅を乗せたときに、それが1キログラムと表示されるように、電子天秤の方を調整するというのである。

　電子天秤は確かに地域ごとに校正をしそうだけれども、体重計はそんな地域ごとに校正をするものなのだろうか。精度保証のために「生産工場で校正をする」ことは当然あるだろうが、使用場所に合わせて校正をしたりするものなのだろうか。

　さらに、「体重計は何を計りたいものなのか」とい宇疑問が頭に浮かんだきた。私たちは「（体の）質量」を計りたいのだろうか、それとも「（体の）重量」」を計りたいものなのだろうか。将来、月面ステーションができて、さらに月面ホテルができ、月旅行ができるような時代になったなら、その月面ホテルのジムにある体重計はどのような校正がされているものだろうか。

　地球で体重42キログラムの人がいたら、月面ホテルのジムの体重計もやはり42キログラムと表示するのだろうか。それとも、そのおよそ1/6の7キログラムと表示するのだろうか・・・？

　月面の観光地にある体重計なら、きっと旅行気分が味わえる「7キログラム表示」を採用しそうだ。けれど、ホテルのジムならどうだろうか。この場合になると、体重管理をしたい人のために、「42キログラム表示」を採用しそうな気もしてくる。

　未来の体重計はどんな風になっているのだろう。・・・いや、違う。「未来の何かがどんなものか」がわからないと思うくらいなら、それを作ることに力を注いだ方が良いのだった。

The best way to predict the future is to invent it.
Alan Kay

■「ブランド」だった「ノートPC」の物語　

　「ブランド」には必ずそのブランドを神格化する伝説があります。たとえば、それが車のロールス・ロイスなら、「砂漠の中でロールス・ロイスが故障した時、ロールス・ロイスはヘリコプターでその車を修理しにやって来て、その上で”ロールス・ロイスは故障しません”という言葉とともに去り、修理代金を請求することを拒否した」といった類の伝説が必ずあります。逆に言えば、そういった物語があって初めて消費商品はブランド品となるのです。

　ノートPCで「ブランド品」と(かつて)言えたものは、どのメーカのどのノートPCだろうか・・・と考えてみました。すると、それはかつての東芝のDynabookとIBMのThinkpadであるように思います。Dynabook(ダイナブック)には、Xeroxのパロアルト研究所にいたアラン・ケイが提唱した、個人が持つ・持ち運び可能なコンピュータ”ダイナブック”の名を受け継いでいる、という物語がありました。そしてまた、IBMのThinkpadには、それこそさまざまな伝説が作られていました。下の動画はそんな「伝説」のひとつです。

　今、「ブランド」と言えるようなノートPCはあるでしょうか。もしあるとしたなら、それはどのメーカのどのノートPCになるのでしょう？

　少し考えて思いつきそうなAppleのノートPCはとても魅力的です。けれど、ここでいう「ブランド」というよりは、「デザイナーブランド」というようなものに見えます。今現在、「ブランド」と呼べる伝説・物語を持つようなノートPCは今の時代に存在するのでしょうか？あるとしたら、一体それはどんな・どのノートPCなのでしょうか。

■「範囲(スコープ)」が決まると「構図(レイアウト)」が決まる　

　目の前にある景色を絵に描こうとすると、「構図（レイアウト）」を決めることがとても難しいことに気づかされます。少し見る方向を変えるだけで、その瞬間に姿を変えてしまう景色を、つまりはありとあらゆる方向に広がっている世界を長方形の平面に描くという作業はとても難しい、と思うのです。

　特に一番難しいと感じることは、ありとあらゆる方向に広がる目に見える世界を適当な「範囲」に切り取る、という作業です。もしも、写真機を手に持っていたならば（あるいはデッサンスケールといった道具を使うならば）ファインダーを覗くだけで「世界を切り取る範囲」を確認することができます。けれど、そういった道具がない場合、目の前の景色は本当にありとあらゆる方向に広がっていて、その限りない世界をどのように切り取るか・どんな範囲で描くかを、自分で決めるしかないわけです。

　その切り取り方を決めるということ、言い換えると、「範囲(スコープ)」を決めるということをとても難しく感じてしまいます。「範囲(スコープ)」を一度決めてさえすれば、「構図(レイアウト)」はきっと自動的に決まると思うのですが、最初の「切り取る範囲・描く範囲」を決めるということが本当に難しくて、できなくて困ってしまうのです。

　もしかしたら、画を描くということだけでなくて、技術的な題材も「範囲(スコープ)を決めれば構図（レイアウト）は自然と決まる」ことが多いのだろうか、とふと考えました。描く（作る）ものの範囲が決まれば、その時に使うことができる技法で描かれるものの配置・繋ぎ方・作り方が自然に決まるのかもしれない、とふと連想しました。さて、実際は一体どういうものなのでしょうか。

■温泉の匂いを味わえるムトウハップ（六一○ハップ）が消える。　

　「温泉の匂いを味わえる温泉の素、武藤鉦製薬のムトウハップ（六一○ハップ）が消える」というニュースが流れていた。

　赤褐色の液体を浴槽の中に入れると、次第に白濁していくようすは見ていてとても不思議に綺麗で、しばらくして広がってくる硫黄の匂いは、まさにどこかの温泉に旅行しているような気分にさせられた。

　「匂い」というものは、首をかしげたくなるくらい、記憶やイメージと直結している。ムトーハップが作る匂いと白濁した湯は完璧に「温泉のイメージ」を再現してくれた。温泉の匂いを味わえる六一○ハップが消えた。

■ビル・アトキンソンの円描画の高速化　

　以前、Andy Heartzfeldの「Revolution in The Valley 」を読んだ。apple Macintoshが生まれる前後の物語であるこの本を読むのにはとても時間がかかった。それを言い換えれば、とても長い時間楽しめた、ということだ。

　たとえば、こんな一節がある。この数行で書かれていることが、どのように使われて、どのように効果を上げたのかを考えながら読んでいかなければならない。つまり、楽しいギミックがたくさん詰まっていて、そんなパズルを解き、読み進めるのに時間がかかるのである。もちろん、それはとても楽しいひとときだ。

「連続した奇数の合計は、常に次の完全平方になる」という事実を使い、Bill AtkinsonはQuick Drawの円描画を早くした。
1=1^1, 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2

　「Revolution in The Valley 」

■片づけやすい部屋はどれ？「名作マンガの間取り」～懐かしのヒロイン編～　

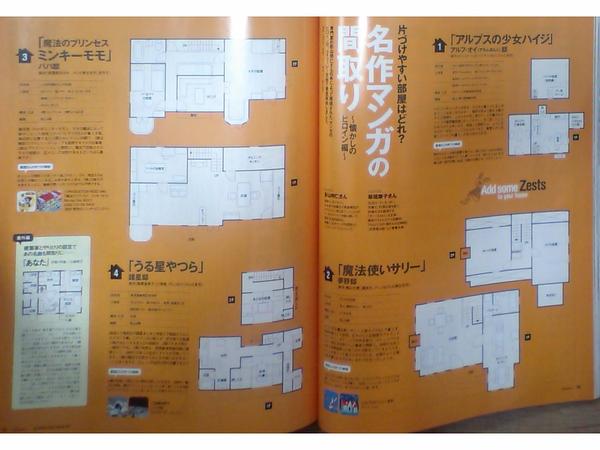
　雑誌 Lucere ! (ルチェーレ) 2008年 12月号（ルチェーレ）を読んでいると、『片づけやすい部屋はどれ？「名作マンガの間取り」～懐かしのヒロイン編～』という記事がありました。「アルプスの少女ハイジ」「魔法使いサリー」「ミンキーモモ」「うる星やつら」といった、名作マンガのヒロインたちが住んでいた家の間取りと、その家（部屋）は片づけやすいのか？といったことを考察している記事でした。

　マンガ(アニメ)のヒロインたちですから、現実にはなくてはならないようなモノたち、つまりは、部屋の中に散らかりがちなものたちも、別にいなくても構わないわけです。だから、部屋が雑然としてしまうこともなく、綺麗な部屋が多いわけです。けれど、その替わりといっては何ですが、収納場所は少なそうです・・・。

　なんだか、この記事の「ファンタジー」さに少し興味を惹かれたので、ここに切り取ってスクラップしておきます。

■「平等の錯覚」文化と「不平等の錯覚」文化　

　以前、異文化間コミュニケーションの話を聞いた。それは、少し想像していたような内容だけでなく、意外に感じること・意外な度合いに感じることもとてもたくさん詰まっていて、とても新鮮に話を聞くことができた。

　新鮮に感じたトピックの一つが、"Illusion of Equality"「平等の錯覚」というものだった。「現実には平等でなく・個人間の差異が多いがために、コミュニケーション上で、ファーストネームで呼び合うなどで、まるで平等が存在するような錯覚を持たせる文化」と「現実には皆が似たり寄ったりの中で、相手の立場を相対的に高くするために、自分を低く見せる文化」という、大きく分ければ2つの文化があって、前者は「平等の錯覚」文化で、後者は「不平等の錯覚」文化である、というものだった。

「平等の錯覚」文化からすれば、「不平等の錯覚」文化が見せる謙遜は「見せかけの不実」に見えてしまうこともある。また、「不平等の錯覚」文化からすれば、「対等・同じ」という位置に居心地の悪さを感じ、ほんの少しの差異に違いを見い出そうとする・・・といった内容が、実に面白かった。

■雑誌の「モノクロ広告」と「カラー広告」の価値は1.5倍しか違わない　

　雑誌の広告費を調べてみると、カラー広告は白黒（1色）広告の1.5倍程度である。雑誌によっては2倍以上違うものもあるけれど、平均的には大体そんな比率になっている。

　カラー印刷が4色もインクを使っているのに対し、白黒印刷は1色だけで刷っていることを考えると、印刷コストの違いが1.5倍に収まるとは思えない。

　けれど、その印刷による「広告」に値段を付けて売りに出そうとすると、つまり価値をお金で計ってみると、モノクロとカラーの価値の差は1.5倍程度に落ち着いてしまうということになるのだろうか。

　モノクロ広告に対する「カラー広告」の付加価値、カラーがモノクロの「5割り増し」ほどだというのは、意外に少ないようにも思える。けれど、「広告として情報を伝えた効果の量」がカラー化することで一体何割増すだろうか、と考えてみると、せいぜい「5割り増し」程度だという数字も納得できるようにも思えてくる。

　雑誌の広告費だけでなく、色々なものを考えたとき「モノクロ」と「カラー」をお金に換算して「価値」という値にしてみたとき、一体どの程度の差になるものだろうか。