hirax.net::inside out::2010年04月

■「マティス」と「状態遷移」と「描かれなかった可能性」　

　マティスの「大きな横たわる裸婦（ばら色の裸婦）」の制作過程を、1935年5月3日の第1ステートから眺め、1935年10月30日の第21ステート、そして、1935年10月30日の最終ステートまで眺めていると、何度も何度も描き直されていることがわかる。その過程を写真で眺め、マティスが何を考えながら、変更・修正を加えていったかを想像することができて楽しい。

　ところで、第1ステートとか、第2ステートと「ステート」といった言葉を眺めていると、「状態遷移(State Transition)」とか「State Flow」なんていうものを連想してしまう。

　たとえば、「ばら色の裸婦」では、私たちが見ることができるマティスのステート（状態）はたかだか22ステートに過ぎない。

　しかし、このステート以外にもたくさんのステートが存在しただろうし、あるいは、存在することはなかったけれども存在する可能性があったことだろう。

　マティスが描いた作業過程を、あるいは、マティスが感じたけれど描かなかった構想を、描かれなかった可能性を、状態遷移図にしたとしたならば、それは一体どんな世界になるのだろうか。

■「対談の準備」と「文章にする作業」　

　松井孝典と南伸坊による対談（というより南伸坊が松井孝典に色々なことを教わるといいう体のインタビュー）をまとめた『「科学的」って何だ! (ちくまプリマー新書) 』を読みました。読んだ理由は、内容、少なくとも章だてが「とても興味ある内容」だったからです。

1. 未来はなぜわかるわけがないのか？～血液型性格判断から科学とは何かといった話題
2. 宇宙の果てはあるのか？～宇宙科学から「わかる」「わからない」といった話題まで
3. 日本はなぜ不合理がまかり通る社会になったのか～選択や格差社会の話題など
4. 人間の欲望はなぜ尽きないのか～豊かとか欲望ととは何か
5. 研究するとはどういうことか？

　しかし、読み進めながら考えたことは、この本の中で語られていることとはまったく関係のないこと、でした。それは、松井孝典と南伸坊と編集者の３人が、どのような風に文章を作ることに関わったのだろうか、ということです。対談の前に「どういうことを話すか」のアウトラインをある程度決めるだろうと思うのですが、そのアウトライン決めを誰がどのように行っていたかを知りたい、と思ったのです。そして、どのように「テープ起こし」をしたテキストを本としての「文章」にしていったかを知りたいのです。

　この本の中では、見事過ぎるくらい南伸坊は「素人役」「うなづき役」に徹しています。「そうですね」「はい」「ええ」「あー」「そうなんですか」…とここまで挙げると、南伸坊の台詞の過半数になるのではないか、と思うくらいです。この「見事過ぎる」度合いは、一体どういうプロセスで作られたのでしょう？

　私の想像では、編集者が「（著者２人に確認した上で）こういう内容で対談してもらいたい」という内容のアウトラインを作り、そのアウトラインを見ながら、南伸坊と松井孝典と編集者が喋ったのだろう、と思います。そして、南伸坊は「素人視線での聞き役」としてり、そして、文章修正の際も、（自身も編集者としての感覚・視線を交えながら）話の流れを邪魔しないように自身の発言部分を単純化し・編集者の言葉なども自身の発言部分に入れていったのではないかと感じます。その一方、松井孝典は、自分の発言部分に間違いがないようにという視点から、自身の発言部にのみ修正を加えていったのではないだろうか、と想像するのです。それが、この対談文章を作ったのだろうか、と想像します。

　…プロの意見など聞いてみたい、今日この頃です。

■「見えるコビト」と「照れるコイビト」　（初出：2005年08月31日）　

「日本科学未来館」で開催されていた「インタラクティブ東京2005(i-tokyo)」の記事を読みました。 記事中で紹介されていた、東京工業大学ロボット技術研究会の「Kobito -Virtual Brownies-」が、とても興味深く感じられました。

　たとえば、「Kobito」(mpg動画や動画のページ)は複合現実感(Mixed Reality, MR)もしくは、人工現実感(Augmented Reality, AR)という言葉で知られるような、現実の世界と「現実ではないが、不思議でリアルなモノたち(働くコビト)」をオーバーラップさせた世界を眺めることができるもので、「なかなか見ることができないモノを実際に眺めることができる」不思議なカメラです。

　この「なかなか見ることができないモノを実際に眺めることができる」不思議なシステム「Kobito」を眺めた後、最近知った「非接触温度測定機能付きデジカメ（製品紹介PDF)」を思い出しました（その非接触温度計付きデジカメが右上の写真のピストル型のグッズです）。

　何でも好きなものを銃口で狙って撮影したり、その銃口で狙った先の対象物の温度変化を調べたりすることができるのです。

　このピストル型デジカメで好きな相手を狙って撮影すると、相手の姿が撮影できるだけではありません。相手が「照れてアツく」なっているのか、それとも、「(あなたに)冷めている」のかを知ることができるわけです。つまり、「なかなか見ることができない相手のお熱（≒自分への気持ち…!?）というモノを実際に眺めることができる」のです。

　当然、ピストルの銃口を自分に向けてみれば、自分が相手に熱くなっているようすだって見せることができるわけです（見せられる方も困ってしまうかもしれませんが…）

　技術系男子は、「相手の気持ちが読めない」とよく言われます。それならば、こんなピストル型デジカメをホルスターに下げ、いつでも必要な時にはピストルを握りしめ、そして温度計のメモリを読み・相手の気持ちを測定してみるのも、「技術系らしくて」良いかもしれません。

　ピストルで狙われた相手がどう思うかはわかりませんし、そんなことをした結果として、ヒュルルル～と気持ちが冷めてしまうかもしれませんが…。

■「過去の卒業アルバム」と「未来の2010年」　

　川合さんのブログを見ながら、ふと思い出したことがある。

　先日、部屋の掃除をした。その時、高校の「卒業アルバム」が出てきた。サイズがとても大きくてかさばるので、捨てるかどうか悩みながら、「あの頃の景色」が映っている頁を、少し、眺めた。そして、捨てるのも変なような気がして、本棚に戻した。

　「生ビール」のポスターを背景に（高校生だから残念なことにビールを飲めるはずはないけれど）、みんなでお好み焼を何かの打ち上げで食べている写真や、学園祭の写真や、四季の校舎を映した景色、つまりは、毎日毎日過ごした風景がそこには写っている。

　その中には、たくさんの同窓生たちがそこにはいる。3年A組から順に頁をめくっていくと、若かりしGaucheの作者もそこに居た。そして、とても不思議な気持ちに襲われた。時が流れるというのは、自然だけれど、とても切なく神々しい。

　「2010年」と聞くと、遥かに先の未来に思える。私たちはそんな世代だ。…いや、違う。そんな世代だったような気がする。けれど、確かに「2010年」という、そんな時代に立っていることが、今でも不思議でしょうがない。

■Windowsディレクトリが壊れて、「Rubyコード」になっていた。　

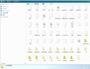
　Windows マシンで、ディスクの一部にアクセスできなくなりました。正確にいえば、ディレクトリにアクセスはできるのですが、そのディレクトリの中身が「ワケがわからない状態」になってしまっているのです。それが、下の画像です。

　何だか、とても奇妙な状態です。まるで、何やらRubyのコードのようなファイル・ディレクトリ名が並んでいる…ような気がします。このディレクトリには、Rubyのコードなどないはずなのですが、何やら、Rubyでスレッドを使って書いたシリアルポート制御プログラムが透けて見えるような気がする感じです。

　こういう現象というのは、一体どういう時に起きるものなのでしょう？そして、どうしたら、こんな現象を回避することができるのでしょうか？

　ディレクトリが壊れるたび、そのディレクトリが色んな言語の化身に変身したら「面白いだろうな」と少し思いおかしくなります。１時間ほど作業した内容がすべて消えたので、結構ショックなのですが、消えたファイル群が「Ruby プログラム」になっていたりしたので、少し楽しくなったのです。

■「メディア・ディペンデント」　

　十年ほど前、ある本の「あとがき」に、こんな文章を書きました。

　インターネットにあふれるWEBページのことを「便所の落書き」と呼んだ人もいます。もし、インターネットのWEBページが「便所の落書き」なのだとしたら、この本は「便所の落書き帳」ということになります。ただ、思いつくままに「便所の落書き」を描き続けていたら、いつの間にかこんな本になりました。

　その後に出した本を考えてみると、たとえば「論理的にプレゼンする技術 聴き手の記憶に残る話し方の極意 (サイエンス・アイ新書) 」は最初から書籍として作ったもので、（本としての）ページの割り付け・ページ内のデザインなど、最初の最初から考え・設計して作り上げたものです（だから…というわけではないですが、この本は、プレゼンが苦手な人から「自分は上級者だ」という人まで幅広い人たちが、それぞれ楽しめる本になっている、と思っています）。

　そしてまた、たとえば（個人的にはとても思い入れのある）「理系サラリーマン 専門家11人に「経済学」を聞く! (Kobunsha Paperbacks Business 17) 」はWEBサイト用の記事として作ったものを、書籍用の手直し・書籍化に際して追加しておきたかったものなどを詰め込み（あるいは削り）、作り上げたものになります。

　もしも、後者を最初から「書籍」として考えて作ったとしたら、一体どういうものになったのだろうか？と思うことがあります。そして、それでは「企画自体通らない」ものだろうな、と思ったりします。やはり、「書籍」と「WEB記事」は違います。メディアによって、作り方も作り始めのカタチもきっと違うのだろうと思います。

　どんなものでも、「（コミニュケーションという）底の部分は同じだよ」と言われるような気もしますが、その舞台・調理法（表現方法）が異なる「メディア」である以上は、やはり違うものにならざるを得ないのかもしれない…と思います。

　そんなことを考えながら、久々に昔書いた「便所の落書き」を読んでみたりしたのです。

■中国名産「コピー商品」のヒミツ　

　前に、「純正A-bike より 8インチ空気タイヤ版 A-bicycle の方が断然イイ！の不思議」で、「（パッチモン＝コピー商品の）8インチ空気タイヤ版 A-bicycle はさまざまな部分で改善がされていて、純正品A-bikeより（現時点では）遥かに"良い移動道具"になっている」と書きました。その時に感じたこと・その時コピー商品って面白いな、と感じたことを、遠藤健治の「中国コピー商品対抗記 (日経ものづくりの本) 」を読んでいて、思いだしました。

　コピー商品の中には、オリジナルの真正品をそっくりそのまま模倣したものだけでなく、そこに造り手のいろいろな意思や、考え、工夫が盛り込まれたものもあるからです。

コピーメーカーは作業性よりも、とにかく低コストになる設計を重視するのです。人件費が低い中国では、作業の効率が多少落ちたとしても、コストが下がるのであれば躊躇せずに部品を削り、その分、人手でカバーする方法を採ることがわかりました。

　「（パッチモン＝コピー商品の）8インチ空気タイヤ版 A-bicycle はさまざまな部分で改善がされていて、純正品A-bikeより（現時点では）遥かに"良い移動道具"になっている」は、たとえば、こんな感じの良い例です。

　まず、コピー商品メーカーは、真正品メーカーの手の届かないところや、企業努力が足りずにつくれなかった市場を見つけ出すことに長けており、その「見えない市場」にコピー商品を投入して市場を開拓すること。

　もう一つは、コピー商品そのものよりも、それで荒稼ぎした利益を再投資するコピー商品メーカーの方が、真正品メーカーにとって脅威であり得るということ。

■あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる　

　あみだくじを作ったとき、「アタリ」がどのような分布になるかは、大雑把には、拡散方程式で解くことができます。もし、あみだくじに横線があれば、右へ行ったり・左に行ったり、酔った人がさまよい歩く酔歩（ランダムウォーク）のように「アタリ」を選ぶことができる場所が、推移するわけです。

　たとえば、拡散方程式を横軸を縦線感覚で離散化し、縦軸は…これまた適当に離散化し、縦方向単位長さ移動するときに、どれだけ左右への移動が生じるか（＝横線が縦線に対して、どの程度の頻度で存在するか）を考えてやり、そしてその離散化された拡散方程式を解いてやれば「あみだくじ」のアタリ分布を計算することができます。

　左端と右端の「境界条件」では、そこで「折り返されたような」動きをするわけですから、ノイマン条件を適用してやればよいことになります。また、時間ステップは、いつものように「循環参照による手動再計算」を用いて実現してやれば良い、ということになります。

　というわけで、エクセルでプロトタイピングして、作ってみたのが下の計算シートです（作成したエクセルシートはここに置いておきます）。たとえば、下のグラフは、アタリが左から３番目縦下部にあった場合に、一体、どの縦線を選ぶの良いかを示す確率分布になっています。今のこの状態なら、左から１番目、２番目、３番目が大体同じアタリ確率になっていて、もう少し細かく眺めてみると、左から２番目を選ぶのが一番アタリをひく可能性が高い、ということがわかります。

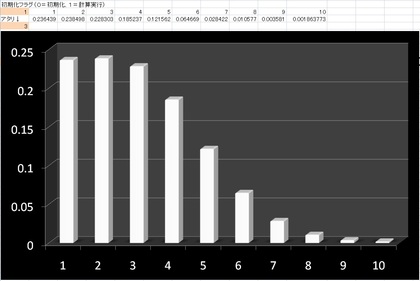
　上の例の場合には、一番アタリをひく可能性が高い線が、アタリのある真上より少し端側に寄りました。この「アタリをひく確率が高い線が端に寄る」傾向は、横線が多いほど激しくなります。…とはいえ、あみだくじを作る時のことを考えると、実際にはあまり横線の数が多くないように、つまり、手抜きあみだくじが多いように思います。

　そんな時は、手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれませんね。

■桜咲く季節の中を「限りない可能性の缶詰」たちが歩いてる　

　早稲田近くに、色んなビールを美味しく安く飲めて、ガラス張りの窓から外をずっと眺めることができる…という３拍子揃った安い店があった。今週、久しぶりにその店に行くと、決して安くはない店になっていた。

　けれど、窓際の席から見える通りはそのままで、料理も美味しかったので、ビールをずいぶん飲んでしまった。「2010年の今だからこそのFortran講座」とか「懐かしきAVSの歴史」といったことを話しながら、ガラスの向こうにある通りを歩く早稲田の新入生たちを眺める。日暮れも過ぎ、照明に照らされた通りを、歩く「可能性の塊」たちを羨望ととも眺める。

　早稲田大学　理工学部の隣、戸山公園の桜は、とても綺麗で、風が吹くと花びらが吹雪のように舞っている。新学期が始まるキャンパスというのは、いつの時も、どこの場所でも、限りない新鮮さが詰まっている。

■「プログラマブルなサイコロ」が欲しい!?　

　Wikipediaのサイコロの項目を眺めていると、各種多様なサイコロが並んでいて、とても面白く思います。特に、面が百個もある100面体ダイスなんていうものを見ると、思わず欲しくなる気持ちを抑えることができません。

　今、一番、私が欲しいと思うサイコロは、面に書いてある数字を書きかえることができる、そんなサイコロです。任意のある「ルール」にしたがった数字群を作りだし、そして、その数字群を各面に表示する、そんなサイコロです。また、できれば、選ばれた面（＝賽の目）以外に書かれている数字はぼんやりとしていてわからない、そんな機能も備えたものが欲しいな、と思っています。

　それなら、数字をディスプレイに表示する電子サイコロでも良いではないか、と言われるような気もします。しかし、電子サイコロだと、「賽を振っている」感じがしないように思われて、今一つ面白くないのです。それでは、「実感・体感」できなくてつまらないのです。

　そんな多面体の形を持って転がすことができる、けれど、プログラマブルで色々な機能を持っている、そんなサイコロがある、という情報、あるいは、この辺りの道具を使ってる来ると良いよ、といった情報などありましたら、教えて頂ければ幸いです。

■「桜吹雪」の「おすそ分け」　

　あまりに桜吹雪が綺麗だったので、「桜吹雪」の「おすそ分け」です。

　桜吹雪があまりに激しく吹いたので、景色の中で激しくたくさんの花びらが舞ったので、私のケータイで撮影した動画圧縮コーデックでは、そのチラツキに対応することができずに、一部見にくい動画になってしまいました。

　桜がたくさん散っているのを眺めているうちに、風が吹き、まさに桜の花が散る「吹雪」のような景色に包まれました。遠くでチラチラ散っている桜の花びらが、自分の方に向かってきて、風の流線に並び沿う桜の花びらの中に立っている、そんな感覚です。 　あるいは、桜の風下にいたので、まるで、雪嵐の中を車を運転して走っているような、桜の花びらが降りしきる雪に見え、そんな錯覚も覚えました。それは、とても心地良く、そして、ほんの少し怖さを感じるくらいの美しさでした。

桜の森の満開の下に立ち、そんな不思議な気持ちに襲われました。そんな気持ちの、おすそ分けです。

■拡散方程式で考える「あみだくじ空間」と「空間ワープ」　

　「あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる」で、あみだくじの（平均的な）動き方を１次元の拡散方程式で解き、アタリを引く確率分布を考えてみました。

　そのことに関して会話をしている中で、「とても新鮮で、着想が面白いな」と感じることがありました。そのアウトラインはいずれ平易な形で紹介させて頂くこととして、ここでは、マニアックで一般受けしそうにない部分を、マニアックで一般受けしそうにない記述で、そのとても面白かった話題を書いてみようと思います。

　といっても、hirax.netを読みに来る人は、これすなわち、一般的ではないとってもニッチ（≠リッチ）な変わりものであるわけですから、そういった方には、ちょっと面白いのではないか・楽しめるのではないか、と思います。

　前回紹介したように、あみだくじのアタリの場所がわかっている時には、その（平均的な）動き方を１次元の拡散方程式で解くことで、（平均的には）ここがアタリやすい場所だ、ということを求めることができます。アタリの場所が中央でなく、横線が十分にたくさんある場合には、アタリが左に寄っているなら左端、アタリが右に寄っているなら、右端がアタリやすい場所になります。横線の数が少なく、アタリが端にそれほど近くない場合には、アタリの真上がアタリの確率が高くなります。

　端っこが確率が高くなるのは、両端がノイマン条件になっていて、両端で折り返される部分多重に重なるから、ということになります。部屋の中のゴミの動きをランダム・ウォークで考えたとき、四隅にゴミが滞留しやすいのと同じ具合です。

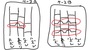
　そんな話をしているとき、「じゃぁ、こんな線を引いたら？」「あるいは、こんなのは？」と言いながら、下図のような２つのケースのあみだくじ（の横線）を引かれました。…これは、ちょっと、とても面白い新鮮で面白い着想だと思いませんか？　確かに、そういう線を、私たちはよく引きます。けれど、そういうことを、年を経るうちに、いつの間にか忘れてしまっていたことに気づかされました。

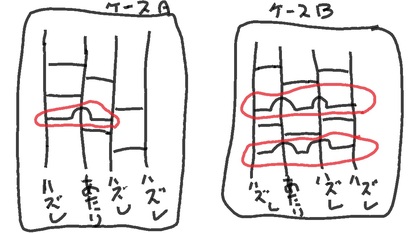
　ちなみに、上図のケースＡのような場合、あみだくじを表現した１次元の拡散方程式で言うと、拡散の速さが速くなることになります。短い時間（あみだくじで言うなら、縦方向の距離で）で、アタリの場所が遠くまで移動していくことになります。つまり、遠くと遠くの空間を結び付ける、これは一種の”ワープ”する線です。

　そして、上図　ケースＢの場合には、左右の両端が、「ノイマン条件」でなく、「周期境界条件」に（線の数がある分だけ）変化していきます。この場合も、結局は、一種の”ワープ”する線であって、それが空間の「反対側」どうしを結び付けている、という具合です。

　結局、これらの”縦線をまたぐ”ような線は、離れた場所を強引に結びつけ、その空間どうしを”ワープ”できるようにすることで、隣り合った空間にさせてしまう、という恐ろしい効果をもっていることを、その当たり前のことを、空間内の拡散現象を表現する拡散方程式を解く、ということをする中で眺めると、ことさらに強く印象付けられます。

　拡散方程式で考える「あみだくじ空間」と「空間ワープ」…何だか、そんなことを考え始めると、ルイス・キャロルの「不思議の国のアリス 」のように、不思議で魅力的な迷路のような空間中を探検しているようで、とても面白い心地になりませんか？

　この話題、もう少し、続きます。

　だってそうでしょう？箱は開けてみなきゃ、中身はわからない。電話は出てみなきゃ、相手はわからない…　少なくとも、旧式の電話はね。
　人の心だってそうよ。…こうして…ノックしてみないと、わからないの。

加納朋子「螺旋階段のアリス 」

■拡散方程式で考える「あみだくじ空間」と「（見えない）時空間ループ」　

　拡散方程式で考える「あみだくじ空間」と「空間ワープ」の続きです。前回は、”縦線をまたぐ”ような線が、離れた場所を強引に結びつけ、その空間どうしを”ワープ”できるようにすることで、隣り合った空間にさせてしまう、という何やら不思議な存在であるのかもしれない、ということを考えてみました。

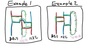
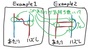
　それでは、次は、こんな場合ならどうしたら良いでしょう？今度は、横線同士が交差していたり(下図のExample1)、同じ縦線同士を繋ぐ線があるような場合(下図のexample2)です。

　あみだくじを拡散方程式で解くときには、縦線の「横方向」が「空間」を意味します。それに対して、「縦方向」はすなわち「時間」を意味することになります。「横線同士が交差する」ということは、異なる縦線の間で「時間」が共通のものでなくなってしまう「奇妙な線」であるように思えますし、「同じ縦線同士を繋ぐ線」はまるで過去や未来へ「タイムトリップ」する「不思議な線」に見えます。

　今回考えてみたいのは、こういったスペシャル技を、ちまり時間軸を捻じ曲げるような「線」をどう扱うか、ということです。「どう扱うか」というのは、「どう考えると、単純に思えるか」ということです。「単純で共通なルールで記述できるか、と言い換えても良いかもしれません。

　なぜかというと、この「線」について考え出すと、少し「スッキリしない」というか「気持ちが悪い」ことが出てくるからです。具体的には、「どの経路を考えてみても、通らない線がある」とか「横線に対して、（両方向に進む経路があって欲しいのに）片方向に進む経路しかない」、あるいは、「線を追いかけていくと、下から上に遡らなければいけない部分がある」ということです（下図参照）。

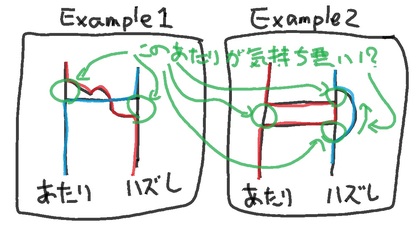
　この「時空間を歪ませるようなスペシャル線」は一体どう扱う・どう考えれば良いのでしょうか？そんなに考え込むことでもないのかもしれませんが、あみだくじというものを考えるとき、「通らない線がある」「横線に対して、（両方向に進む経路があって欲しいのに）片方向に進む経路しかない」「線を追いかけていくと、下から上に遡らなければいけない部分がある」というのは、あまりに「おさまりが悪いこと」であるように思われます。

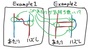
　そこで、こう考えてみることにしました。下図のように、時間を捻じ曲げるているような線の部分には実は「縦線が隠されている（そういう仮想縦線を考えてみる）」と考えてみるのです。そして、その（仮想）縦線は最下部と最上部が繋がっていて、最下部からさらに下にさがると…アラ不思議、最上部にワープして、そこから下に降りていく、という具合に考えてみるのです。それが、下の図です。

　すると、例外的な現象に思えていた不思議なことが、ごく当たり前の普通のあみだくじに見えてきます。あみだくじを辿る線は、いつでも下方向にしか移動しません、つまり、「線を追いかけていくと、下から上に遡らなければいけない部分がある」という現象は消えますし（仮想線の最下部でも、（仮想線の最下部と最上部が連結されているだけで）その空間上は下に落ち続けているのみです。）、「（いろいろな経路を考えたとき）通らない線」というものもなくなりますし、「横線に対しては、両方向に進む経路が必ずある」という、ごくあたりまえのあみだくじに思えてきます。（下図参照）

　というわけで、横線同士が交差していたり、同じ縦線同士を繋ぐ線がある時には、そこには実は見えない縦線が隠されていて、その縦線はたとえるなら上下両端が繋がったことで「明確な端を持たない」ということだけが特殊だ、と考えてみるのです。「実は目には見えづらい空間（縦線）があり、そこでは時間軸は永遠のようでなぜかループしている」というわけです。

　こんな風にあみだくじを、あみだくじの「スペシャル線」から考えてみると、何だか不思議なくらい惹かれます。そして、考えていくうちに、変に思えていたものが、いつの間にか、ひとつの綺麗な星座のように見えてきます。それは、とても面白い感覚です。

　数字がバラバラに書いてあって、その数字を順番になぞっていくと最後に絵ができる"Connecting Dot"ってパズルがあるじゃない？　バラバラだったりしても、途中で間違っているように思えたりしても、色々と続けていたら最後に何か浮かび上がってきたりしたら、それで良かったりするのかな？って時々思ったりするの。

種ともこ　「どこかの学園祭コンサートで」

　（目の前にいる人・目の前にある悩みを）ボーと見ていると、おもしろいものが見えてくる。その面白いものが見えてくることを"コンステレーション"と呼びます。"コンステレーション"というのは「星座(を意味する言葉)」です。

河合隼雄 「河合隼雄 その多様な世界―講演とシンポジウム 」

　星が散らばっている時、その星を結んだ瞬間が一番楽しい。

浅草キッド　水道橋博士

■気付かないことを教えてくれる解説や説明　

　久世光彦　主催の「久世塾 」単行本を読んでいると、滅多に手放しでドラマを褒めることがないという久世光彦が「ビューティフルライフ 」を、シナリオが上手い、演出が上手い、そして、木村拓哉が上手い、映像監督が、カメラマンが、関わった人すべてが上手い、と非常に評価していた。

　僕はあのドラマを非常に評価するのです。めったにドラマは褒めませんけれども、あれはみんながうまいのです。

特に、印象的だったのは、木村拓哉についてこう書いていた部分だ。

　それと木村拓哉がうまい。あの木村は半端でなくうまかった。（中略）そのぶんをちゃんと木村が背負ってやっている。あれが何か妙な間で、悲しいのか悲しくないのかわからないじゃないかというようなことがうまいのです。

　こういった解説がされて、ようやくわかること、というものは数多くある。こういう解説文を読んだ時には、自分では汲みとることができなかったもの、あるいは、自分では見ることができない「それがどのように生み出されたか」を知ることができて、少しトクをしたような気持ちになる。そして、もう一度、それを味わい直したくなる。

　例えば、「ビューティフルライフ」は、いかにもトレンディドラマの代表みたいな木村拓哉と常盤貴子をくっつけて設定を合わせただけだろうとけなす人もいるけれども、そこには戦争があってドラマになっていた。それは見てわかる。ディレクターと北川悦吏子さんとの間でかなり熾烈な戦争があったような気がします。

久世光彦

■雑貨ショップで「レーザーライト」の内部を覗く　

　雑貨ショップに、音に連動して適当な模様を描くレーザライトがありました（右上のようなものですが、右上のものとは違い、回折格子などは取り付けられていないものです）。気になったので、店頭でレーザライト内部を覗いてみることにしました。

　レーザー照射口周りを外して、中身を覗いてみると、緑色レーザーと赤色レーザーに、小さなガルバノミラー2個とミラーが1個の光学系を付けたような具合になっていて、マイクからの音入力でガルバノミラーを動かしている、という具合です。

　なぜ、内部を見たかったかというと、レーザ駆動部分と、ガルバノミラー駆動部分を改造して、（好きな模様を描くことができる）格安レーザースキャナを作れそうかを確認してみたかったからです。このレーザライトが、9千円くらいだったということもあり、部品代を考えるとリーズナブルに思えたのです。

　内部を覗いた結果、これは改造してみる価値があるかもしれない、と判断したのですが、さらに、今度は自分の財布の内部を覗いた結果、買うのをあきらめてしまいました。

　100円ショップにでも行って、部品をかき集め、レーザースキャナを980円くらいで作れないものでしょうか。スピーカーを買って格安ガルバノミラーを作り、レーザポインターを買って、自由自在に絵を描くことができるレーザースキャナを980円くらいで…作れないものでしょうか。

■「あみだくじ無限ループ」を生み出す「（見えない）時空間ループ」　

　「なぁ、あみだくじで無限ループって作れるとおもうか？」という面白いスレッドを読みました。

　なぁ、あみだくじで無限ループって作れるとおもうか？

　けれど、普通のあみだくじでなく、拡散方程式で考える「あみだくじ空間」と「（見えない）時空間ループ」で扱ったような、横線同士が交差していたり、同じ縦線同士を繋ぐ線があるような、普通ではないけれど「よくやりがちな」あみだくじなら、どうでしょうか。しかも、前回考えたように、そういう特殊線には実はゴールとスタート地点が繋がっている縦線が隠れているとしたら、どうでしょうか？たとえば、前回描いた下のような例です。

　「ゴールとスタート地点が繋がっている縦線」があるとするならば、「終わらないあみだくじ」は存在する。けれど、そのスタート地点もゴール地点も表には出てこない（隠されている）からその存在を意識しないだけ、ということになります。具体的には、上図に緑色の線で描いた経路です。この経路は、「終わらない」「無限ループ」になっています。ただし、その経路は（あみだくじの参加者にはスタート地点が）見えない「仮想縦線」なので、その存在に気付かないだけ、という具合です。

横線同士が交差していたり、同じ縦線同士を繋ぐ線の後ろに「仮想縦線」が隠れていると考えてみると、あみだくじの「（スタート地点とゴールとの）一対一対応といった特性はそのままに（それ以外の特性も前回考えたようにそのままに）、「あみだくじの無限ループ線」が存在しうる、ということになります。

　何だか、ちょっと面白いと思いませんか？

■「チョンマゲ」始めました。　

　お笑いコンビ「ロザン」の片割れ、「芸人として成功するために、相方の宇治原を京都大学に入れた」管が綴る「京大芸人 」を読んでいて面白かったのが、この一節だ。

　席に座りなにげなくまわりを見渡すと、僕の右斜め前に信じられない光景が目に入った。サムライがいた。
　正真正銘のサムライがいた。茶色の着物を着て、腰に刀を差していた。頭を見てみるとかつらではなく、地毛でチョンマゲを結っていた。
　そのサムライはおもむろにカバンからパソコンを取り出して何やら作業を始めた。まるで、（中略）Ｂ級映画のワンシーンを見ているみたいだった。

　このごろ都にはやるもの、勧誘、貧乏、一目ぼれ。葵祭の帰り道、ふと渡されたビラ一枚。
　腹を空かせた新入生、文句に誘われノコノコと、出向いた先で見たものは、世にも華麗な女(鼻)でした。
　このごろ都にはやるもの、協定、合戦、片思い。祇園祭の宵山に、待ち構えるは、いざ「ホルモー」。「ホルモン」ではない、是れ「ホルモー」。戦いのときは訪れて、大路小路にときの声。
恋に、戦に、チョンマゲに、若者たちは闊歩して、魑魅魍魎は跋扈する。

■「さがしもの」は何ですか？見つけにくいものですか？　

　何年か前、「自分探し」が流行った。「自分」というものがどういうものなのか、よくわからないままに、そんなよくわからない「自分」というものを探すブームがあったような気がする。

　何かを求める人がいるなら、何かに対するニーズがあるのなら、つまり、需要があるのなら、そこに供給者が現れる、というのがよくある状況だと思う。

　自分を探す人が数多くいるのなら、「（その人たちが求める）自分」を、よりどりみどりに並べ売る、そんな供給者が現れるに違いない。そんな「自分」を売る店は、さぞかし繁盛するに違いない。「自分」というものは、きっと売れる「商材」に違いない。

　…と、そんな風に考えてみると、本屋に並ぶ自己啓発本は、まさにそんな「（その人が求める）自分」を売る本であるかのように思えてくる。本屋に並ぶ本の多くは、自分探しをする人のために、「その人が求める自分」を提供するための本なのかもしれない。それを、言い換えるなら、本屋で私たちがそんな本を手に取るとき、無意識のうちに（かつて流行った）「自分探し」をしているのかもしれない。

　「自分探し」ブームの頃、同時に、「自分隠し」ブームも流行っていたような気がする。「自分隠し」ブームというものがあったとしたなら、そこには一体どんなものを供給するものが現れるのだろう。何かを隠す森のようなものを供給するものが現れるのだろうか。

　それとも、供給者でない何かが、そこでは必要とされるのだろうか。

■「NET USE」コマンドと「Google」と　

　「PerlでWindowsネットワーク内のフォルダ内ファイルを操作したい時はどうする？」と知人に聞かれた。いくつか案を出した後、最終的に答えたのは、「WindowsのNET USEコマンドを使って、Windows内でネットワーク上ディレクトリ・ファイルをローカルにあるものと認識させて、Perlからは何も考えずに普通にアクセスするのではどうでしょうか？」という”とりあえず”な”逃げ案”だった。知っていると、苦労しないで済むWindowsのコマンドというものが、結構あるようにも思うけれど、この―Windowsのファイル共有やプリンタ共有と，ローカル・ドライブやローカル・プリンタといったデバイスへのマッピングを管理する―NET USEコマンドは、古いWindowsネットワーク内で作業する時には、知っておいても損はないコマンドのひとつだと思う。

　とはいえ、そんなコマンドを活用できる環境がいいのか悪いのかはよくわからない。先の知人は、梅雨が始まる前くらいに、Googleに入社するという。

　WindowsのNET USEコマンドを使い、Perlを使う、そんなことは新たな環境ではきっともうないことだろう。そんな切り貼りだらけの、不便で不細工な工作をするようなことはもうないに違いない。

　桜咲く季節は、新しいものと出会う。無限の可能性にワクワクさせられる。そして、桜の花が散った後の新緑が見える頃には、出会いがあれば、別れもある。

■正規表現と「美しいコード」　

　しばらく前のことだったと思う。正規表現の書き方の話題になり、「美しいコード」とか「目的に対する実装のバランス」といった話になった。

　その時、「コンパイル(NFA->DFA)にどの程度の時間がかかるか」という観点からのアドバイスを受けた。これまで、そういった基本的なことを考えたこともなかったので、今さらながら、そのアドバイスを消化するために、正規表現とNFA・DFAについて、さらってみた。

　DFA:Deterministic Finite Automaton=決定性有限オートマトン、やら、NFA：Nondeterministic Finite Automaton=非決定性オートマトンといった文字列を眺めながら、こんなワクワクさせられる面白いことを、なぜ今まで楽しむことができなかったのだろうと、そんなことを切実に感じさせられた。

　なお、オートマトンの日本語訳は、自動機械であって、自動羊肉ではないらしい。

■「星新一　一〇〇一話をつくった人」の350頁から次の頁にある言葉　

　最相葉月の「星新一〈上〉―一〇〇一話をつくった人 (新潮文庫) 」を読んで、坪内祐三が書いた書評のラストがこの文章である。

　先に私は、誰もが星新一を読んだことがあるはずだ、と書いた。逆にいえば、みな、星新一を卒業してしまう。
　それから星新一の苦悩がはじまる。それがこの評伝の一番の読み所とも言えるラストスパートだ。

「文庫本を狙え！」 616　週刊文春　「文春図書館」

　下巻の三百五十頁から三百五十一頁にかけてを私は何度も読み返している。

　この文庫本は、三年前に出た単行本「星新一　一〇〇一話をつくった人 」を文庫として出版したものだ。文庫版は、先日出たばかりの本だから、「私は何度も読み返している」というのは、ひと桁程度の「何度か」なのかもしれないし、あるいは、単行本を読んでの「何度も」なのかもしれない。

　「星新一　一〇〇一話をつくった人」は単行本で読んだ。単行本を読みながら、最相葉月が書く星新一の物語は、愛が感じられていい、と思いつつ読んだ記憶がある。この単行本の一体何ページ目が「文庫本の下巻の三百五十頁から三百五十一頁」にあたるのだろう。坪内祐三が何度も読み返している、と書く文章は、一体、単行本ではどの頁にあるのだろう。

■タンポポの花は、夜閉じる　

　昼間、道を歩いているとタンポポの花が満開に咲いていた。思わず、太陽の光の下で黄色に輝くタンポポの一群を写真に撮った。

　ところが、夕方、同じ場所を歩いていると、あれだけ強烈に景色を彩っていたはずのタンポポが見当たらない。

　これは一体どうしたことだろうか…と思いながら、その辺りの草むらを、よくよく眺め直してみる。すると、そこには花をキュッと蕾（つぼ）めて閉じたタンポポたちがいた。

　昼間あったはずのタンポポの花が消えたのではなくて、ただ満開に咲いていた花たちがその顔を隠していただけだったのだ。

　タンポポの花は、夜閉じる。花びらを閉じて蕾のような状態で眠る。タンポポの花は朝になると咲き、夕方近くになるとそっと閉じる。そして、花が咲き終わり時間が経つと、白い綿毛を輝かせ、それを飛ばす。

　タンポポの花は、２から３日間咲き続けます。しかし、夕方になると、次の朝まで花を閉じます。

今までずっと、こんな不思議で魅力的なことに気付かないまま過ごしてきた。…もしかしたら、こどもの頃はそんなことを当たり前のように知っていたのかもしれないが、それなら、いつの間にかそんな秘密を忘れていたのかもしれない。

　気付かないだけで、そういうことが実はとても多い、のかもしれない。

■眠る「睡蓮（スイレン）」　

　「タンポポの花は、夜閉じる」ことが新鮮だったので、同じように夜眠る花を探してみた。すると、たとえば、（私たちがよく眺める種類の）スイレンもそういう「夜は閉じて眠り、昼には花を開く花」である、と知った。だから、「睡眠の蓮」で睡蓮と名づけられたという。

　そういうことを知ると、睡蓮で彩られた公園の池を見るとき、これまでとは違った見方をするようになるように思う。たとえば、それが昼の池なのか、それとも、夜なのかということを意識しながら眺めるようになりそうだ。

　「睡蓮」という言葉を見ると、クロード・モネを思い出す人も多いだろう。モネが一番描いたものが、「睡蓮」である。さまざまな色彩で、睡蓮が浮かぶ景色をモネは眺め、絵筆で描き出している。「光の画家」と呼ばれたモネは、光に照らされた風景がきらめくようすを、写真よりリアルに描き出している。

　睡蓮には、夜眠り昼咲く種もあれば、昼眠り夜起きる種もあるという。光を描いたモネが見たたくさんの「睡蓮」は、一体、どんな種類の睡蓮なのだろうか。それは、陽の光の下に咲く睡蓮だろうか、それとも、月光の下で咲く花だろうか。

■続　エクセルにおける循環参照時の計算順序　

　「エクセルにおける循環参照時の計算順序」で書いたような反復計算がおこなわれるのは、あくまで「循環参照」がされているセルに対してである。この「循環参照がされているセルに対して」ということは、えてして忘れてしまいやすい。つまり、シートの一部に「循環参照」がされているセルがあれば、シート全体が反復再計算されるのだ、という勘違いをしてしまいやすいように思う。

　反復計算がされるのは、あくまで「循環参照」がされているセルだけ、である。「循環参照」がされているセル群だけが反復計算の対象になり、それらのセル群の（前回計算結果との）変化量が所定値以下になるまで、それらのセル群に対して再計算を（前回記事のような順番で）行うことになる。

　シート上で「循環参照がされていないセル」に関しては、再計算されることはなく、初回の計算時の値がそのまま使われる。だから、たとえば、どこかのセルに乱数値を返すようなものが含まれていたとしても、つまり、計算ごとに明らかに変化するようなセルが含まれていたとしても、（循環参照がされていない限りは）そのセルの値は初回の計算で決まり、変化することはない。考えてみれば、当たり前の話だが、油断するとその当たり前を忘れてしまう。

　えてして、反復計算が行われる時には、シート全体が再計算されるという勘違いが頭の中に忍び込むことがある。そして、その間違った先入観のもとに、エクセルでプロトタイピングをしたりすると、思ったような計算がされず、ラピッド・プロトタイピング、すなわち、素早くたたき台を作とうと思ったはずなのに、多量の時間を費やす羽目になってしまったりする。

　エクセルの基本的な機能だけを、しかし、その基本的な機能を深く解説した本を読んでみたい。

■Ruby で書いた計算プログラムの実行速度　

　「入門レベルの問題ですが」と前置きをされた上で、プログラミングの「問題」を出された。「5分間でコーディングして下さい。あと、プログラムの実行時間が2秒を超えるなら誤答です」と言う、厳しいオマケの言葉付きで、そんなお題を出された。

　とりあえず、頭を雑巾のように振りしぼり、単純そうな解法のRubyコードを書いてみた。…しかし、2秒で計算を終えることはどうしてもできそうにない。少なくとも、その100倍以上の計算時間がかかる。

　「これは見当違いの解法アルゴリズムだったか…」と思いながら、出題者におそるおそる提出してみると、「アルゴリズムは合っている」という。とりあえず、「解法を思いつかない」という最悪の自体は避けられたが、それにしても、もう少し高速化して提出したかった。

　Rubyで書いたのは、こんなコードだ。このRubyコードを高速化しようと思うなら、どのようにすれば計算時間を短くすることができるだろうか。また、同じ解法を他言語で実装した場合、Rubyコードとどのくらい計算速度が違ってくるものなのだろうか。

def makeRect(n)
  data=[]
  n.times{ data＜＜[rand(),rand(),rand(),rand()] }
  return data
end

def makeMesh(rects)
  xg=[]
  yg=[]
  rects.each do |xt,xb,yt,yb|
    xg＜＜xt＜＜xb
    yg＜＜yt＜＜xb
  end
  xg.sort!
  yg.sort!
  mesh=[]
  (xg.length-1).times do |x|
    (yg.length-1).times do |y|
      cx=(xg[x]+xg[x+1])/2
      cy=(yg[y]+yg[y+1])/2
      area=(xg[x+1]-xg[x])*(yg[y+1]-yg[y])
      mesh＜＜[cx,cy,area] if area＞0
    end
  end
  return mesh
end

rects=makeRect(1000)  
mesh=makeMesh(rects)
area=0 
mesh.each do |x,y,a| 
  rects.each do |xt,xb,yt,yb|
    if xt＜x&&x＜xb&&yt＜y&&y＜yb
      area+=a
      break
    end      
  end	
end
puts area

　「お題」を書け、と言われそうですが、どこぞのプログラミング・コンテストで出題されるかもしれないということもあり、「お題」自体は書かないでおきます。また、「お題」がわかりづらいように、コメントを削除してあります（といっても関数名・変数名から、ある程度は想像できそうにも思いますが）。というわけで、回答コードをもとに、「お題」の内容を逆に想像してみると、そしてより良い解法を考えてみたりするのも、面白いかもしれません。ちなみに、上記コードで、makeRect(1000) としている部分は、問題が訂正され、数百程度になりそう、ですね。

■Mac OSXをインストールできるVirtualBox 3.2.0 Beta 1　

　VirtualBox 3.2.0 Beta 1がリリースされました。見どころのひとつ、とても興味深い部分は、"Experimental support for Mac OS X guests"という点です。つまり、Mac OS XをゲストOSとして、バーチャルマシンとして、任意のホストマシン（ＯＳ）上にインストールすることができる、という機能です（下のスクリーンショット参照）。

　「試験的」と断り書きがついているにせよ、正式にMac OS XをゲストOSとしてインストールすることができると謳った仮想PCソフトウェアは、このVirtualBox 3.2.0 Beta 1が初めてだと思います。VirtualBox上でMac OS Xを動かした場合、どのような機能が使え、どのような動作速度になるのでしょうか。

　なお、VirtualBox 3.2.0 Beta 1は”Windows 7 64 bit”がホストOSの場合、動作しないという既知のバグがあります。

■野球の硬式ボールと軟式ボールの重さの違い　

　陽の光が柔らかく当たる公園横のグラウンドで、米軍の関係者らしき人たちが野球をしていた。ボールを久々に投げてみたい気持ちになり、一瞬だけ混ぜてもらい、ノックを受け・送球をした。

　その後、野球に興じる人たちを横目で見ながら、「速球を投げられない」と同行者にこぼすと、「硬式と軟式のボールの重さ」の違いについての話をしてくれた。硬式ボールの方が軟式ボールより重いので、硬式ボールを使うプロ野球の選手が軟式のボールを投げた時には、空気抵抗のため硬式ボールほどの速球を投げることができないのだ、という。

　なるほどそうだったのかと思い、帰ってから、ボールの重さの違い・規格を確認してみた。すると、硬式ボールが141.7-148.8gとなっていて、軟式ボールは134.2-137.8g（A号）となっている。なるほど、10%弱ほども重さが違うのであれば確かに球速に影響を与えるに違いない。

　それにしても、春が過ぎ初夏の前、梅雨が来る前のこの季節、野球をしている人たちは心から気持ち良さそうに見えた。「幸せって何だっけ？」という問いへの答えのひとつが、こんな景色だったりするのかもしれない。

■始まる前からよく喋ると、たいていダメ　

先日、聴いたこんな言葉が心に残っている。

「始まる前に、よく喋っている場合はたいていダメですね」
「逆に、全然喋らない人の方が化けますね」

　どんなことであっても、「貯める」ということは大事なのかもしれない。小さな川を堰（せ）き止め作るダムのように、吐き出さず貯めないとできないもの、ということもありそうだ。

　この「始まる前に、よく喋っている場合はたいていダメですね」というひとことは、何だかとても的確なアドバイスのように思える。…問題は、「始まる前から喋る場合はたいていダメ」というのは、「肝心な時以外は口を開かなければい」ということを必ずしも意味するわけではない、というところだろうか。