hirax.net::inside out::2010年05月

■女子学生の恋人選び方　実験編　

　少し前、女子学生相手に、こんな実験をしてみた。実験として出した「お題」は、「これから20人が登場します。順々に人が登場します。といっても、登場するのは”あなたとの相性を数値で表したもの”だけです。あなたは、（順に出てくる相性数値を眺めながら）この人を恋人に選ぶ、と決めたところで、手を挙げてください。あなたは、手を挙げた瞬間の相手を選ぶことになりますから、すでに登場した前の人を選ぶことはできませんし、それ以降に登場する人を選ぶこともできません」というものである。この「お題」を出した時に、どのような選び方をするのかを知りたかったのである。

　ちなみに、女子学生に見せる数値は、２０人１セットの実験を始める前に、平均値と分散を適当に決めた正規分布乱数である。２０人１セット内では平均値と分散は変化しないとはいえ、その平均値や分散は、相性数値を眺める被験者はわからない、という条件である。

　面白かったのが、女子学生が全員「最初の数人分の数値に関してはただ眺め、どういう相性数値が出てくるのか、つまり、平均値はどの程度でバラツキはどの程度なのかを、最初の数人を眺め・見極めた上で、相性数値が上位に入る人のところで”手を挙げる”という選び方をした、ということだった。とても興味深い事に、被験者はみな同じような選び方をしたのである。この選び方は、数学が導く理想の選び方、とほぼ同じである。

　その結果、被験者全員が「（コンピュータが用意した）20人の相手の中から相性数値がベスト３に入る相手を見事に選んだ」のだった。

　女子学生の直感（あるいは、推論・予測能力というべきか）は、恐るべき精度を持つものだと驚かされたのである。

■女子学生の恋人選び方　”あなたも挑戦してみよう”編　

　今日は、女子学生の恋人選び方　実験編でやってみた「これから20人が登場します。順々に人が登場します。といっても、登場するのは”あなたとの相性を数値で表したもの”だけです。あなたは、（順に出てくる相性数値を眺めながら）この人を恋人に選ぶ、と決めたところで、手を挙げてください。あなたは、手を挙げた瞬間の相手を選ぶことになりますから、すでに登場した前の人を選ぶことはできませんし、それ以降に登場する人を選ぶこともできません」というお題を、あなたも試してみる・体験してみることができるようにしてみました。

　下にあるのが、その道具（フォーム）です。JavaScriptの正規分布乱数関数を使い、20人分の「相性数値」をボタンを押すたびに順々に（1人分の数値づつ）出力します。出力される「相性数値」は数値が大きい方が「相性が良い」ということを示します。20人分まで出力すると、一旦止まり、また初期に戻ります。

　正規分布乱数の平均値と偏差は固定されています。だから、この記事のソースを眺めれば、どんな正規分布乱数であるかがわかってしまうことになります。つまり、どんな「人たち」が登場するのかを、おおよそ予想することができてしまいます。とはいえ、そんなカンニングはせずに、ぜひ、順に並ぶ数値群から、どんな人たち（数値群）が登場するのか想像してみてください。

そして、20人目まで（20人目を含む）の間で、「この人（数値）を選ぶ」と（相性数値が出た瞬間に）決めてみてください。そして、さらに、自分が選んだ数値が20個の数値の中で一体上から何番目に位置していたか、ということを調べてみてください。その結果が、あなたの「選び方能力」ということになります。

　「（コンピュータが用意した）20人の相手の中から相性数値がベスト３に入る相手を見事に選んだ」女子学生たちを、あなたは超えることができたでしょうか？それとも、全然ダメだったでしょうか…？

　ところで、登場する相性数値から平均値・分散を直感で刻々予想し、あなたが想像した予想平均値・分散の変化推移を眺め直してみても面白いかもしれません。そうすると、自分がどんな風に考え・予想をしていたかを、自分自身で改めて知ることができ、ちょっと不思議な気持ちになることでしょう。

■ダイソーの「自転車タイヤ・パンク修理セット」を使ってみた　

　100円ショップのダイソーの「自転車タイヤ・パンク修理セット」を使ってみました。もちろん、「よし、今日こそ使おう！」と思ったから使ったわけでなく、昨日、情けなくも道路の段差でタイヤをパンクさせてしまったので、しょうがなくパンク修理をすることにしたわけです。「自転車タイヤ・パンク修理セット」100円ナリをダイソーで買ったのは、良くも悪くも時流に沿って、お財布の中身が大幅なデフレーションをし続けているからです。それはまるで、パンクした自転車のタイヤ・チューブのようにヒュルヒュルと萎（しぼ）むデフレが続けているからです。

　自転車屋さんに行ってパンク修理をしてもらうと、1000円くらいの修理代金がかかります。その1000円が（ゴムのりやゴムパッチが何回か使えることを考えると）100円以下でできるのは、財布も私もうれしい限りです。しかし、その値段の差はゴムパッチの品質が（自転車屋さんが使うものと100円ショップで売っているものでは）違うだろうことや、何より自分自身の人件費（時間）をゼロ円として、勘定に入れていないことが大きいように思います。

　…ということは、100円ショップで買った道具を使って自分で修理するのは経済学的に眺めると一体どういうことになるんだろう？とか、こういうお財布の選択が景気には一体どんな影響を与えるのだろう？とちょっと考えてみたりする今日この頃です。

■IronRubyとJavaScriptでMathematicaフロントエンドを書いてみる（修正してみる）　

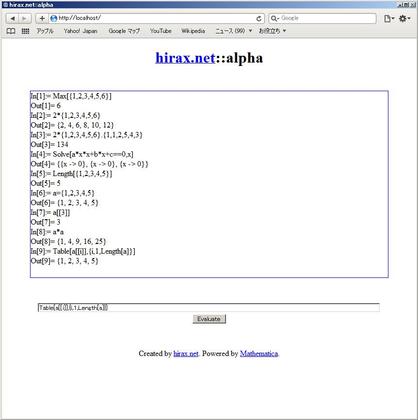　以前、IronRubyでMathematicaのフロントエンドを作ってみました。以前作成したコード(JavaScript部分)にバグがあったこともあり、今日は少し手直しをしてみました(Mathematica Playerでも動作するコードになっていますが、Mathematicaのライセンス上、PlayerでないMathematicaに付属するKernelとともに使うことを前提にしています)。今日書いたコード・ファイル類は、ここに置いておきます(mathnode.rbの6行目には、あなたの環境のMathematicaKernel.exeパスを記述してください)。また、（ファイルに添付してあるリンク先から）Wolfram.NETLink.dll　をダウンロードし、スクリプトと同じフォルダに入れておく必要があります。

　今日修正した部分は、「処理する数式をエンコードするJavaScriptコード(encodeURIComponent関数) を書き忘れていたこと」「WEBページのカスタマイズをしやすいように、RubyコードとHTMLコードを分離したこと」「（前述対応およびスレッドが１つしかないことによるデッド・ロックを防止するように）Webrickのコードを書き変えたこと」になります。ちなみに、前回作成したコードだと、処理する数式をきちんとエンコードしていないため、演算子などの処理に誤りが生じ、たとえば、3+2を解かせると、（恐ろしいことに）6という答えが返ってきてしまいます。

　また、今日作成したHTMLコード（index.html）の冒頭部分には、スタイルシート(css/hatena/hatena_ryukyu-green/hatena_ryukyu-green.css)読み込みの記述がありますが、これは、はてなの（GPLライセンスにもとづいている）スタイルシートを使うことができるようにしてあるためです。ですから、それらのスタイルシートをダウンロードしてない場合には、その部分をコメントアウトしておいて下さい。

　このことを逆に言えば、（こんな風に）CSSとJavaScriptを使って自分の好きなようにカスタマイズできるMathematicaフロントエンドを作ることができる、ということになります。JavaScriptとCSS、そして、Mathematica（とRuby）を使い、自分好みのデザインや（外部サービスと連携させるような）各種機能を備えた数式処理環境を作成してみるのも、面白いかもしれません。

■続　IronRubyと JavaScriptでMathematicaフロントエンドを書いてみる（修正してみる）　

　IronRubyと JavaScriptでMathematicaフロントエンドを書いてみる（修正してみる）で書いたコードをさらに使いやすくしてみることにします。といっても、私が書いたコードの「使いにくい」部分を、もう少しまともに「使いやすくする」というわけです。

　自分で使ってみて、一番最初に「使いにくい」と感じた部分は、ボタンを押さない処理が行われない、というところです。そこで、昨日のコードに付属する"index.html"中の＜input type="text"＞の部分を、

＜input type="text" name="q" id='q' size=100 onChange="calc()"＞

　プリポストプログラムを作るのは、自分の書いたコードが「見た目」や「動き」に直接反映されるので、わかりやすく楽しいものです。…というわけで、（私と違い）JavaScriptを使い慣れている人、あるいは、（私と同じく）JavaScriptを使い慣れていない人でも、こんな具合で、色々いじってみると楽しいかもしれません。そして、斬新なフロントエンド環境を作ったりしたならば、その楽しさをおすそ分けして頂ければ幸いです。

■上岡龍太郎と岡部まり　

　「探偵ナイトスクープ」の秘書役だった、岡部まりが参院選出馬のため、降板するという。

　ずっと昔、20年以上前から、気になっていることがある。それは、初代の探偵局長の上岡龍太郎が、彼が忌み嫌った心霊・霊媒師・超能力・オカルトなどと、文化・信仰、あるいは、宗教をどのように分けて考えていたのだろう？ということだ。そして、「探偵ナイトスクープ」で心霊ネタの扱いに対して立腹し、鋭い言葉を放つ上岡龍太郎に対し、その横にいる岡部まりはどんなことを考えていたのだろうか？ということだ。その二人とを、私自身ずっと好きだったこともあり、ずっと気になっていた。

上岡：「霊がいる、いないということを何も解明せず、単にふざけたVTRを流しただけで、TVに出せば除霊師が認知されたと勘違いしてしまう。面白かったら良い訳ではない。面白くても、それによって何らかの影響力を与えてしまう。それを常々、考えないといかん」
岡部:「確かに仰る通りなんでね・・・」

探偵ナイトスクープ「オカルト嫌いによる騒動」

　岡部まりには、彼女自身の考え方・信じるもの・信じる対象 があり、上岡龍太郎には、また別の考え方・感じ方・信じないものがある。この収録の瞬間に、特に、岡部まりが何を考え・何を感じていたかを、つねづね知りたいと思い続けてきた。

　あの時、彼女はどんなことを考えていたのだろう。そして、今、彼女と彼はそれぞれどんなことを考えているのだろうか。

■ラブホテルのバックヤードから見上げた空　

　関東で、テキ屋のバイトをしていたのと同じ頃、関西でラブホテルのバイトをしていた。夏の祭りの昼と夜、水に浮かぶスーパーボールをすくおうとする子どもを眺めていたのと同じ頃、おとなたちが訪れる春過ぎのラブホテルの中で、昼や夜に空を眺めていた。

　暇な昼は、駐車場から青空を眺め、夕方から数時間の忙しい時間には、部屋の回転を速くするために「客から退室するという電話が入ると、客からは見えないスペースに立ち、部屋を出た客が部屋の入口を見えない場所に移動する瞬間には部屋に入る。客が駐車場から車を出すと同時に、次の客へ青信号を出し、駐車場に入れる。次の客が駐車場に車を留め、部屋に行きつくまでの時間に、部屋の掃除を完了させる。

　短時間で部屋の掃除を終わらすために、部屋に入った瞬間に、まずは風呂に行く。湯船にお湯が入っていたら、何よりさきにお湯を抜く。バスタオルで湯船や便器を拭き、ついでにそのバスタオルでコップを拭き、清掃済みの半透明袋でコップを覆う。ベットの上のシーツは、使いまわせないようであればシーツを交換し、そうでない限りは、シーツを四方から引っ張りビシッと貼る。掃除を終えて身を隠した瞬間、客の影が廊下の向こうに見える時もある。

　そして、夜、12時を過ぎ「休憩タイムから宿泊タイム」へと変わることを確認し、自転車でラブホテルの駐車場を出る。駐車場の出入り口のビニール暖簾を自転車で抜け、高速道路のインターチェンジを横目に、京都駅の方角、北に向かう。夜空に浮かぶ、東寺のシルエットや京都タワーを眺めながら、さらにペダルを漕いで北に向かう。

　テキ屋をしながら見上げた空も、ラブホテルのバックヤードで待ち時間に見上げた空も、どちらも日常のようで非日常のようで、時間割で割り切れないような不思議な感覚で、それがとても心地良かった。

■Rubyで数独ソルバを書く（が、動かない…）　

　数独で見るRuby（と Mathematica）のパワーと表現力を参考に、Rubyで数独ソルバを書いたのですが、まともに動作してくれません…。もちろん、「書いた通りに動作している」わけですから、書き方が悪いわけですが、どうにもこうにも上手く書くことができません。そこで、Rubyコードをここに貼り付け、とりあえず「わかる」ようになるまで、放置しておこうと思います。

require 'pp'
class Array
  def replaceAtXY x,y,v
    a=self.dup;a[y][x]=v;a;
  end
end

def search b
  (!b.flatten.include?(0)&&!pp(b)&&exit)||(deepen b)
end

def deepen b
  l=b.flatten.index 0; x=l%9; y=(l/9).floor
  candidates(b,x,y).each{|v| 
    search b.replaceAtXY(x,y,v) }
end

def candidates b,x,y
  cand=Range.new(1,9).to_a
  ym=3*(y/3).round;xm=3*(x/3).round;
  (ym..ym+2).each {|i| (xm..xm+2).each {|j| 
    cand.delete b[i][j]} } 
  b[y].each{|v| cand.delete v}  
 # (0..8).each {|i| cand.delete b[i][x] }
  cand
end

search [[0,0,0,0,0,7,0,9,0],
[0,3,0,0,2,0,0,0,8],
[0,0,9,6,0,0,5,0,0],
[0,0,5,3,0,0,9,0,0],
[0,1,0,0,8,0,0,0,2],
[6,0,0,0,0,4,0,0,0],
[3,0,0,0,0,0,0,1,0],
[0,4,0,0,0,0,0,0,7],
[0,0,7,0,0,0,3,0,0]]

[[1, 2, 4, 5, 8, 7, 6, 9, 3],
 [5, 3, 6, 1, 2, 9, 7, 4, 8],
 [7, 8, 9, 6, 3, 4, 5, 1, 2],
 [2, 4, 5, 3, 1, 6, 9, 7, 8],
 [3, 1, 7, 5, 8, 9, 4, 6, 2],
 [6, 8, 9, 2, 7, 4, 1, 3, 5],
 [3, 2, 5, 4, 6, 7, 8, 1, 9],
 [1, 4, 6, 3, 9, 9, 5, 2, 7],
 [8, 9, 7, 1, 2, 5, 3, 4, 6]]

■Rubyで数独ソルバを書いてみる　

　「Rubyで数独ソルバを書く（が、動かない…）」のコードを見直したところ、なぜ動かなかったがわかりました。理由は簡単で、Arrayに2次元行列を格納しているときには、 "a=self.dup" というコードでは2次元行列のディープ・コピーがされない、ということでした。ごく初歩的な間違いです。

　そこで、コードを修正し、また、少しコード量を短くしてみたのが、下のRuby ソースです。関数は全部で3つ、「解答であれば出力し、そうでなければ探索をする」という関数 "find" と、1～9野数字で埋まっていない部分（すなわち、0が入っている部分）を、周りおよび該当行・列を見た上で候補を上げ、候補数値で埋めた上でさらに探索を再帰的に行う関数 "deepen"と、候補数値群を作りだす関数、"candidates"です。

require 'pp'
def find b # isGoal or serach (b=boad)
 ( !b.flatten.include?(0) && !pp(b) ) || deepen(b)
end

def deepen b
 l=b.flatten.index 0; x,y=[l%9, (l/9).floor]
 candidates(b,x,y).each{ |v| a=b.map{|c| c.dup};a[y][x]=v;find a}
end

def candidates b,x,y
 h,v=[3*(y/3).floor, 3*(x/3).floor]
 (1..9).to_a-b[y]-(0..8).map{|i| b[i][x]}-
     (h..h+2).map{|i|　(v..v+2).map{|j| b[j]}[i]}
end

find [[0,0,0,0,0,7,0,9,0],
[0,3,0,0,2,0,0,0,8],
[0,0,9,6,0,0,5,0,0],
[0,0,5,3,0,0,9,0,0],
[0,1,0,0,8,0,0,0,2],
[6,0,0,0,0,4,0,0,0],
[3,0,0,0,0,0,0,1,0],
[0,4,0,0,0,0,0,0,7],
[0,0,7,0,0,0,3,0,0]]

[[1, 2, 3, 4, 5, 7, 8, 9, 6],
 [4, 3, 1, 5, 2, 9, 6, 7, 8],
 [2, 7, 9, 6, 1, 3, 5, 8, 4],
 [7, 6, 5, 3, 4, 8, 9, 2, 1],
 [5, 1, 4, 9, 8, 6, 7, 3, 2],
 [6, 8, 2, 7, 9, 4, 1, 5, 3],
 [3, 5, 6, 8, 7, 2, 4, 1, 9],
 [9, 4, 8, 1, 3, 5, 2, 6, 7],
 [8, 9, 7, 2, 6, 1, 3, 4, 5]]
[[1, 2, 3, 4, 5, 7, 8, 9, 6],
 [4, 3, 1, 5, 2, 9, 6, 7, 8],
 [2, 7, 9, 6, 1, 3, 5, 8, 4],
 [7, 6, 5, 3, 4, 8, 9, 2, 1],
 [5, 1, 4, 9, 8, 6, 7, 3, 2],
 [6, 8, 2, 7, 9, 4, 1, 5, 3],
 [3, 9, 6, 8, 7, 2, 4, 1, 5],
 [9, 4, 8, 1, 3, 5, 2, 6, 7],
 [8, 5, 7, 2, 6, 1, 3, 4, 9]]
・
・
・

　コードは、およそ12行ほどですから、（「数独で見るRuby（と Mathematica）のパワーと表現力」の10行にはとてもかないませんが）比較的コンパクトと言えそうです。また、本来のアルゴリズムとは関係のない、2次元のArray要素を検査・操作する部分に行数を費やしてしまっているので、（そういったよく使いそうな）メソッドをArrayクラスに追加するライブラリを書きたくなります。

　それにしても、プログラムのアルゴリズム・コードを作り・書くという作業は、とびきり面白いパズルを解くのと同じ楽しさ（そして辛さ）を与えてくれます。ハマると、止められません…。

■初心者向け「Mathematicaで書かれた数独ソルバ」　

　「Rubyで数独ソルバを書いてみる」では、Mathematicaで書かれた数独ソルバを前に、そのコードをRubyで写経してみました。

　MathematicaのコードをRubyに翻訳しようとするときに、一番最初は、Mathematicaでよく使われる「短い書き方」からでは、（私の単純で小さなあたまでは）動作の手順を見通しづらかったので、まずはじめにしたことはMathematicaのコードを冗長な記法で打ち直すことでした。私が写経がてら打ち直した、（自分向けの）冗長なMathematicaのコードが下のようになります。

　"deepen"関数は上記の"冗長"コードではずいぶんと長くなっていますが、オリジナルのコードでは下記のように実に簡潔です。

deepen[x_] := With[{pos = First@Position[x, 0]}, 
  Or @@ Map[search, (ReplacePart[x, pos -> #] & 
      /@ candidates[x, pos])]]

　一体、どういう記述の仕方であれば、自分にとって「わかりやすく・書きやすい」のだろうか？と、少し、頭を捻っているところです。

■VirtualBoxでMacOSXゲストマシンを作ってみる　

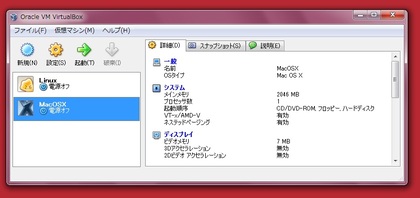
　仮想PCソフトウェアのVirtualBoxのBETAバージョンは、ゲストマシンとしてMac　OS Xをインストールする機能を謳っています。そこで、（Mac　OS Xをインストールするところまではしませんでしたが）MacOSXゲストマシンを作ってみました。

　VirtualBoxでは、Mac OS Xの仮想PCとして、64 bit　カーネルの"Mac OS X 64 bit"と（実際のMacintoshであれば、6+4押し起動時に相当します）、互換性重視の32bit カーネルの"Mac OS X"という2つの設定で仮想PCを作ることができます。その設定は、仮想PCの「設定」タブから、いつでも切り替えることができるようです。

■オブジェクト指向のRubyに、数式処理ソフトウェアMathematicaの機能を自然な形で取り入れてみよう!?　

　「Rubyで数独ソルバを書いてみる」でMathematicaで書かれたコードをRubyに翻訳してみました。その作業をしながら考えたことは、「Mathematicaの機能をRubyに自然に取り込むとしたら、一体どういう言語仕様になるのだろうか」ということです。すべてのものが「リスト」であり、基本的に関数型言語であるMathematicaの機能を、多くのものを「オブジェクト」として扱うオブジェクト指向のRubyに（Rubyになじんだやり方で）取り入れるとしたら、一体どんな記述になるのだろう？という疑問です。

　RubyとMathematicaを繋いだものとして、Ruby/Mathematicaがあります。Ruby/Mathematicaで「Cos(x)をxで積分した結果」を求めるコードは下のようになります。

math=Mathematica::Mathematica.new.start
puts math.eval_foreground('Integrate[Cos[x], x]')

　そこで、頭の整理がてら、もしもMathematicaのコードをRubyに溶け込ませるとしたらどうなるかを考えながら、「Mathematicaの機能を(.NETベースの)IronRubyに取り込むコード」をつらつら書いてみました。

　書いたコード（ライブラリ）は後述することとして、まずは、そのコードを使った例を紹介してみることにします。たとえば、「Cos(x)をxで積分した結果」を求めるなら、こんな感じの記述になります。

p 'x'.Cos.Integrate 'x'

　あるいは、'2 x + 3 == 0'という方程式を、xについて解くなら、

'2 x + 3 == 0'.Solve 'x'

　同様に、「（Rubyネイティブの!）配列"[[1,2,3],2,3]"について、それぞれのサイン関数を求め、数値化する（その結果を出力する）コード」なら、こんな具合です。

p ([[1,2,3],2,3]).map.Sin.N

p 3.Times(10).Plus 5

　さて、オブジェクト指向のRubyにMathematicaの機能を自然な形で取り入れるために、試しに書いてみたコードは、下のようになります。

　…下のコードを要約すると、メソッド名が見つからない場合に呼ばれるmethod_missingで、「見つからないメソッドがあった場合には、その命令をMathematicaに投げちゃえ」というだけのコードです。つまりは、単に(Ruby上で)未知のメソッドを「右(Ruby)から左(Mathematica)に受け流す」という「ムーディ勝山」方式…ということになります。しかも、オブジェクトの総本山、Objectクラスにその「ムーディ勝山」メソッドをいきなりMix-inしてしまう…という、とんでもないコードです。一発ネタ的コードとして、楽しんで頂けたら幸いです。

# 2010/05/12 jun hirabayashi jun@hirax.net

class Mathematica
  require 'Wolfram.NETLink'
  include Wolfram::NETLink
  # ここにMathKernel.exeへのパスを記述する
  PAR="-linkmode launch -linkname 'C:...\\MathKernel.exe'"

  def Mathematica.to_m(array)
    strArray=[]
    array.each do |item|
      if item.kind_of? Array
	strArray＜＜Mathematica.to_m(item) 
      else
	if item.kind_of? String
	  strArray＜＜'"'+item+'"'
	else
	  strArray＜＜item
	end
      end
    end
    '{'+strArray.join(',')+'}'
  end
  
  def Mathematica.to_a str
    require "JSONParser" 
    jsonParser=JSONParser.new
    s=str.gsub(/, ([^{]{1})/,',"\1')
    s=s.gsub(/([^}]{1}),/,'\1",')
    s.gsub!(/\{([^{]{1})/,'["\1')
    s.gsub!(/([^}]{1})\}/,'\1"]')
    jsonParser.parse s    
  end

  def Mathematica.callback
    proc {
      @kernelLink.EvaluateToInputForm 'MVClose[]',0
    }
  end

  def initialize()    
    ObjectSpace.define_finalizer self,Mathematica.callback
    @kernelLink=MathLinkFactory.CreateKernelLink PAR
    @kernelLink.WaitAndDiscardAnswer
  end
  
  def do(q)
     @kernelLink.EvaluateToInputForm q,0
  end
  
end

module MathematicaModule
  def method_missing(name, *args)
    $mathematica=Mathematica.new unless $mathematica
    if self.kind_of? Array
      obj=Mathematica.to_m(self) 
    else
      obj=self 
    end 
    if name.to_s
      results=$mathematica.do( [name,'[',
          ([obj]+args).join(','),']'].join('') )  
    end
    return results
  end

  def To_a
    Mathematica.to_a self
  end
end

class Object
  include MathematicaModule
end

■続 オブジェクト指向のRubyに、数式処理ソフトウェアMathematicaの機能を自然な形で取り入れてみよう!?　

　「オブジェクト指向のRubyに、数式処理ソフトウェアMathematicaの機能を自然な形で取り入れてみよう!?」で書いたコードに、Mathematicaの「リスト」をRubyの配列に変換するメソッドTo_aを追加しておきました。たとえば、

pp ('i'.Table '{i,1,3}').To_a.join('-')

"1-2-3"

　MathematicaのリストからRubyの配列に変換する部分は、下のようなコードになっています（全体像は先日の記事を参照ください）。

  def Mathematica.to_a str
    require "JSONParser" 
    jsonParser=JSONParser.new
    s=str.gsub(/, ([^{]{1})/,',"\1')
    s=s.gsub(/([^}]{1}),/,'\1",')
    s.gsub!(/\{([^{]{1})/,'["\1')
    s.gsub!(/([^}]{1})\}/,'\1"]')
    jsonParser.parse s    
  end

　こんなことをしてみると、MathematicaとRubyを繋ぐために、JavaScriptで使うJSONを利用してみたりすると…何だか言語間が繋がってくるような気がして、何だか少し楽しいですね。

　なお、今回使用したJSONParserが文字列内にカッコ([])があるときに、JSON配列のパースを行えないため、今回のコードでは、Mathematicaの出力結果リスト中に[]があるときには、たとえばSin[x]といったものがある場合には、このTo_aメソッドは利用できません。それが、暗黙に自動で型変換を行わせていない理由です。

■Hodrick-Prescott フィルタのナゾ!?　

　経済オンチ解消のため、まずは景気動向を眺めてみようとふと思い、景気データを解析する手法について調べてみました。その作業をする中で、景気データから周期成分を取り除き、トレンド成分を導く手法の"Hodrick-Prescott filter"が気になり、頭から離れなくなりました。

　" Hodrick-Prescott filter"というのは、離散的な時系列データy(t)が与えられたとき、そのトレンド成分をτ(t)とすると、下記のような評価関数を最小化するようにτ(t)を定める、というものです。ちなみに、y(t)、および、τ(t)は、景気データを対数(log)値で示したものになります。

　この式を眺めれば、第二項は二階微分を中心差分でとり、その結果をデータ全域にわたり積分したものだということがすぐわかります。つまり、（景気データを対数軸で示したときの）直線からのズレ・ジグザグ度合いです。その直線からのズレ度合いに定数λを掛けたものです。ちなみに、このλは離散データが三か月ごとのデータであれば、（多くの場合）1600が使われます。もしも、サンプリング間隔が密になれば、二階微分の結果が小さくなるので、それを補うように大きな値が用いられます。また、サンプリング間隔が疎であれば、二階微分の結果は大きくなるということで、ラムダには小さな値が用いられます。たとえば、サンプリング間隔が１年なら、（多くの場合…は以下省略します）λは100が用いられますし、月ごとのデータであれば、14400が用いられますが、これは「二階微分値に対し自乗をとっている」ことを考えれば（その自乗分に比例定数λを合わせようと思うなら）、なるほど、と思えるはずです。

　また、第一項目は、トレンド成分と実データのズレ＝取り除きたい周期成分、をデータ全域にわたり積分したものです。ということは、このHodrick-Prescott フィルタは、「実データにトレンド成分がなるべく沿うようにした上で（第一項）、トレンド成分がなるべく対数軸上で直線になるようにする（第二項）」というものであることがわかります。そして、その第一項目と第二項目に対するバランス（評価関数の重み）が、第二項に掛けられてるλで与えられる、というわけです。λが大きければ、「実データから”周期成分”を大きく取り除く＝対数軸上で直線になるようにする」ことになりますし、ラムダが小さければ、「対数軸上での直線からのズレが大きくなってもいいから、実データに沿う＝”周期成分”をあまり取り除かない」ということになります。

　解説論文を読んだ印象は、この式のλは「米国景気データをもとにした合わせ込み（上手くつじつまがあうようにλを設定する）」で求められた結果であり、また、「対数軸上で景気動向は直線になる」という前提（背景）のもとに作られている、という具合です。（参考：「トレンドとサイクルの分解」の「実際には単位根の問題や成長率を問題にすべき点から、対数階差を原系列データにほど こしてから分析すべき」という辺り）

　このHodrick-Prescott フィルタが頭から離れなくなったのは、「Hodrick-Prescottフィルターをかける前の変数変換」という、専門の先生による記事を読んだからです。この記事では、Hodrick-Prescottフィルタは「そのままの値」にかけるのか、「対数変換した値」にかけるのか、それは「対数変換した値」が一般的だろう、と説明された上で、

　そのままの値にH-Pフィルターをかけた結果と対数変換した値にH-Pフィルターをかけた結果は基本な形状は変わらないはずですが、スケールが変わってしまうので注意が必要ではないかと思います。

　疑問を何とか形にしてみると、それはHodrick-Prescottフィルタの評価関数が「対数軸上で景気動向は直線になる」という考えのもとに作られているの（ように見える）に対し（しかも、評価関数の第二項目は単に景気のトレンドを（与えられた軸で）直線にしようとする働きしか持たないにも関わらず）、線形値に対してHodrick-Prescottフィルタを掛けた場合、「対数軸上で現した場合に景気動向が直線になる」ようなトレンド成分が得られるのだろうか？本当に「基本な形状は変わらない」のだろうか？という疑問です。この評価関数を最小化しようとした場合に、対数軸でも線形軸でも「基本な形状は変わらない」のはどうしてだろう？という疑問です。

　きっと、式を追いかけてみれば、あるいは、いくつかの例を解いてみれば、この疑問は解消する（理解できる）はず…と思えます。というわけで、とりあえず、この「Hodrick-Prescott フィルタのナゾ!?を解く（きちんと理解する）」ことを、メモ帳のTo Doリストに書き入れておこうと思います。

■ハードウェアのサービス・メニューをいじってみよう!?　

　多くのハードウェア、あるいは、ソフトウェアには「隠された機能」が搭載されているものです。それはたとえば、デバッグや調整をするための特殊メニューといったものです。サービス・メニューとかサービス・モードといった名称で、YouTube内を検索すると、そういった機能をいろいろ眺めることができます。たとえば、トヨタ　Lexusのサービス・メニューや、BMWのサービス・メニューといった車に搭載された機器の「隠された機能」や、iPodのサービス・メニューなど、多くの隠された機能を知ることができます。

　下の動画は、hpのプリンターに隠されている"Easter Egg"のゲーム機能です。

　イースター・エッグ（Easter egg）は、コンピュータのソフトウェア・書籍・CDなどに隠されていて、本来の機能・目的とは無関係であるメッセージや画面の総称。ユーモアの一種。 多くの場合、企画・開発スタッフの一覧などが隠されているが、ゲームなどの場合もある。アニメーションや音楽を伴って表示されることもある。

イースター・エッグ

　身の回りにある、ありとあらゆるハードウェア・ソフトウェアに、こうしたサービス・メニューや"Easter Egg"が隠されています。あなたの身の回りにある機器・日頃眺めている機器の”サービス・メニュー”をYouTubeで探してみると面白いかもしれません。秘密のメニューをいじってみれば、まるでスパイ映画の登場人物になったような気持ちになることができるかもしれません。

■柔道技にはタイミングが重要だ!?　

　衆議院内閣委員会での三宅雪子議員の話ですが、遠くから足元を写した動画を見れば、(A)押されて、よろめいた初鹿明博議員の右足が(B)三宅雪子議員の少なくとも右足を後ろから払いのけ、足を後ろから払われた（おそらく(C)押しつ押されつでバランスが不安定になっていただろう）三宅雪子議員が前に転ぶ、という順序だということがわかりやすく納得できるように思います。
　これら、(A)(B)(C)のいずれも、結果を生んだ原因と言えば原因ですが、三宅議員の転倒は、それらが組み合わさって生じた偶然が生んだ現象という気もします。また、(A)の遠因もさらにあるわけですから、足元を写した動画を丁寧にテレビで放映し直せば、話が想像話で空回りせず、すぐに話題が収束するだけような気がします。

　タイミング次第で、格闘技の技は見事なくらいに決まるのだろうな、とこんな動画を見るとつくづく感じさせられます。大の大人を見事なダイブをさせてしまうことも、呼吸が合えばいともたやすくできるのだろうな、と思わされます。

■ジャックの枝豆　

　先日、畑に大豆を植えた。ビールならぬ発泡酒のつまみを安上がりに済ませようと、枝豆として塩茹（ゆ）でにしようと考えているからである。

　数日前、大豆の芽が地面から顔を出してきた。そこで、土を割って生えてきた大豆の芽をマクロ撮影してみると、何だか巨大な建造物をミニチュア写真風に撮影したかのようだ。これは何だっけ、そうだ童話の「ジャックと豆の木」とともに描かれている挿絵のようだ。

　そのあくる朝、ジャックは目をさまして、もう夜があけたのに、なんだか暗いなと思って、ふと窓の外を見ました。するとどうでしょう、きのう庭に投げ捨てた豆の種子（たね）から、芽が生えて、一晩のうちに、太い、丈夫そうな豆の大木が、見上げるほど高く伸びて、それこそ庭いっぱい、うっそうと茂っているではありませんか。

　今度、ガラクタ箱から小さな人形でも探して、豆の芽の横に置いて写真を撮ってみることにしよう。そうすれば、置いた人形はジャックに見えて、豆の芽は空高く伸びる「ジャックの豆の木」のように写るに違いない。…と、そんな風にただ眺めているだけではダメだと、「ジャックと豆の木」は語るのだけど。

　豆の木を見て、どこまでも登って行こう、と思ったことが、ジャックの運が開く始まりだったのです。それを、ただぼんやりと、不思議だなあと思い眺めて過ごしていただけなら、…あなたたちは、あいかわらず貧乏のまま暮らしていたはずです。

■大人がすなる植物観察日記　

　朝、顔を出した豆の芽（ジャックの枝豆）は、日暮れが近づく頃には、色も形も大きさも変わっている。朝は薄い黄緑色だったはずが、濃い緑色になって、下の方を向いていた芽も上を向いている。

　小さい頃、学校の宿題で植物の観察日記を描かされたような気がする。すくすく伸びる植物を眺め記録をつけるという作業は、大人の方がハマるのではないか、と思わされる。自身が育ち盛りのこどもより、なかなか成長しない大人の方が、意外に嬉々として観察日記をつけそうな気がする。

　ジャックの豆の木は一晩で雲の上まで伸びていったが、豆の芽がみるみる間に姿を変えていくさまを眺めていると、あのジャックの豆の木も、荒唐無稽な話ではないな、と考えたりするのである。

■「ピカソ」を記憶のままに描いてみる　

　ふと、「ピカソ」を記憶のままに描いてみるとどうなるかと思い、テキトーに描いてみた。描いてはみたけれど、頭の中にイメージした題材が「ピカソ」であることすらわからない絵になってしまった。これではまるでシャガールか、…いやそんなことを言うとシャガールが窓の外から怒って襲ってきそうだ。とにかく、これ以上ないくらい下手くそなラクガキだ。

　記憶にまかせて、「有名な画家」の絵を描いたら、一体人はどんな絵を作り出すものだろうか。たくさんの人が、たとえば、「ピカソ」の絵を描いたら、どんな絵の集合ができるのだろう。

■ペットボトルのキャップで小さな小さな「家庭菜園」　

ペットボトルのキャップの中で、 種を発芽させ・成長させる 「Merry Farming」キットを買ってみたい。これ以上ないくらいに小さくて、どんな狭い部屋でも、その小さな「畑」をひとつ増やすことも気軽にできる。ペットボトルのカラフルなキャップに、バジルの種を植え、日光が差しこむ窓の近くにでも置いて飾ってみたくなる。

　キャップだから省スペースで、持ち運びもカンタン。何よりキュート。バジルやブロッコリー、マスタードなど育てられるものもたくさん。カラフルなキャップ を集めて、自分だけのキッチンガーデンも良いかも！

■「目の前に飛び出す立体映像」は…老眼にはツラい!?　

　3時間ほど液晶シャッター眼鏡をかけ、スクリーンに映し出された立体画像を見ながら打ち合わせをした。最初は、画面から目の前に飛び出す物体を新鮮に感じていたのだが、ふと恐ろしいことに気がついた。目の前に物体が飛び出してくるたびに、どうも頭を後ろに持っていこうとする自分がいる。飛び出す物体を眺めようとするとき、その物体との距離を、無意識に離そうとしている自分に気がついた。

　近くのものを見ると、目が疲れるように感じる・・・つまり、老眼が入ってきていると感じている。しかし、そんな老眼というものは眼のピントを合わせる筋肉が老化し、近くのものにピント合わせをすることだけがツラいのだと思っていた。だから、立体テレビのような「実際には遠くに映し出されているものを」眺めるのであれば、たとえ老眼が入ってきても全然関係ないと思っていた。しかし、哀しく、恐ろしいことに、「目の前に飛び出す立体映像」も…老眼にはツラいようだ。立体映像は、そんなところは真に迫らなくとも良いのに、悲しいかな、「近くにくると見えづらい」というところまで真に迫っているのである。

　「目の前に飛び出す」けれど、老眼の眼に優しい、眼の筋肉に優しい「立体映像」ができないものだろうか。

■「注文の多い料理店」を好きな人・苦手な人　

　食べること・飲むことが好きだ。自分が飲食するのも好きだし、人が美味しそうに食欲大魔神になっているのを見るのも好きだ。…しかし、それはあくまで、食べたいもの・飲みたいものを、自分たちのペースで口に入れている場合である。

　秋葉原で、軽く夕飯を食べようと、串揚げの店に入った。最初に、苦手なものを聞かれ、「苦手なものはありません」と答えると、もう食べられなくなったらストップと言ってくださいと言われ、ひたすらにおまかせで色々な「串揚げ」が次々と出てくる。どれもこれも、間違いなくとても美味しいのだけれども、食事の場としては何だかとても良くない。

　全席カウンター形式というのも、好きなタイミングで好きなものを注文できる限りは最高だが、「苦手なもの」以外は自分の選択肢がないとなると、いや、唯一頼めるメニューが「ストップ」しかないとなると…何だか自分が人工餌をひたすら食べ続けるブロイラーになったような気持ちになってくる。50cmの眼の前に、ひたすらに具を揚げ続ける人がいると、その人に聞こえないように、「この店、今一つ良くないから、すぐ出て違う店に行きません？」と、連れの人たちにその意思を伝えることも難しい。

　また、一緒にいる人たちと話をしていて、串を出されるスピードと食べるスピードが合わないと、揚げた串が食べる前に冷えてしまうこともある（それはとても残念だ）そして、自分の気持ちだけでなく、食べ物にも悪いし、料理を作る人にも悪い。客の回転率を上げ、売上を上げることに関してはとても良いシステムだと思うのだが、それ以外のことを考えると、すべてに悪いシステムであるような気がする。

　美味しい串揚げをお腹いっぱい堪能し「ストップ」と言い、満足して店を出た。しかし、こういうシステムの店には二度と入るまい、とも誓ったのである。「料理の食べ方」が指定されているような注文の多い料理店には、これから気をつけようと思う。

■赤青メガネで眺めるPowrePoint立体スライド　

　立体ディスプレイで科学現象を解説する打ち合わせをした後に、赤青（シアン）メガネで立体的に眺めることができるPowerPointスライドを作ってみたくなりました。スクリーンから眼の前に飛び出してくるように見えるプレゼンテーション・スライドを見たならば一体どんな風に見えるのだろうか？と思ったのです。

そんな「赤青メガネで眺めるPowrePoint立体スライド」が下の画像です。黒背景デザインのスライドに、PowerPoint Slides in 3Dや、アナグリフ写真を貼り付けてみたのです。

赤青（シアン）メガネが手元にある人ならば、右目に青（シアン）色、左目に赤色で、眺めてみると面白いと思います。基本、王道からはとても離れた、まさに「色もの」プレゼン・スライドですが、意外に立体感を楽しく眺めることができると思います。

　PowrePointに加法混色の色エフェクトを実装させることができたなら、立体の飛び出すデザイン・テンプレートを作ってみると楽しいかもしれません。PowrPointの裏技を色々いじってみたくなる、今日この頃です。

■「陰日向に咲く」　

　ずっと観たいと思っていたけれど、ずっと観ないでいた、「陰日向に咲く」を観た。

　物語というのは、こういうものなのかと思う。そして、映像というものはこういうものなのか、と知る。

文字を綴（つづ）った文章で、描かれる対象が小刻みに入れ替わってしまえば、その意味を追うことができないものになってしまいそうだ。しかし、それが映像ならば、私たちはそこに写る映像の印象とともにそれを見分けつつ、そして、それと同時に、それをひとつに溶け合った大きな物語として感じることができるようになる。

　物語の縦糸を紡ぐのは、人と人とが出会うことの奇跡。偶然オレオレ詐欺の電話に出た老婆と心を通わせ、自らの過去と向き合うことになるシンヤ。寿子は、シンヤと共に母のかつての恋を追う過程で、自らの殻を破っていく。鳴子は雷太との、リュウタロウはモーゼとの出会いをきっかけに、新しい生活に足を踏み入れる。そして、みゃーこを一途に応援し続けるゆうすけにも、思いがけない「再会」が…。

　小さな出会いが重なり合い、やがて忘れかけていた家族の絆や初恋の切なさが浮き彫りになっていく。そして、彼らが明日への一歩を小さく踏み出す瞬間に見せる清々しい表情。そこに待ちうけるのが必ずしも「日向」でないことはわかっていても、人生に無駄な出会いなど決してないと、深くうなずかされるはず。

■iPadで眺めるHTML5 Youtube　

　iPadでYouTubeを眺めようとする場合、Flashが搭載されていないために、試験的に提供されているHTML5を介してを眺めることになる。そうすれば、レンダリングのバランスが崩れている部分もあったりするけれども、普通にYouTubeを楽しむことができる。YouTubeに格納されている膨大な動画群は、ネットが持つ大きな資産なのだから、それらをiPadで楽しむためにはこのHTML5経由のYouTubeは欠かせない。もしも、HTML5経由でYouTubeを眺めることができなかったとしたら、iPadを使ってみようとも思えないくらいである。

　ところで、iPadはどれだけ売れるのだろう。どのようなコンテンツが提供され、どんな用途に使われ、そんな風に楽しむためには一体どのくらいの維持費がかかるものだろうか。iPadは、生活の中にどんな姿をして入ってくるのだろう？

■トラックポイント付きの小型ワイヤレス・キーボードをiPadで使う!?　

　iPadでbluetoothマウスを使う記事を読む。

So the other day, I gave BTstack Mouse app a go on my jailbroken iPad and was pretty impressed with the result. Not only did it worked with Apple Magic Mouse, but also with almost all the other Bluetooth enabled mice I had. For those of you who don’t know, BTstack Mouse is a free utility which was first released earlier this year for jailbroken iPhones and iPod touch.

　持ち運ぶことを意識した、トラックポイント付きの小型・ワイヤレス・キーボードがないものだろうか。できれば、右画像の「lenovoのThinkPlus USBトラベルキーボード ウルトラナビ付（英語）」のタッチパッド・パームレスト部分をなくし、bluetooth対応にしたようなキーボードがいい。そんなキーボードがあったなら、それをiPadに繋げれば、手をキーボードから離さなくとも操作できる環境ができあがる。

　しかし、トラックポイント付きキーボードで操作するiPad…では、まるでiPadを使う意味がないような気もする。こんなことを考えるなら、キーボードから手を離したくないと考えるなら、iPadでなく英語キーボードのThinkpad でも使えばよいのである。

　iPadを上手く使いこなしている人を横から観察してみたい。そして、その使いこなし術を学んでみたい、と思う。

■タブレット・デバイスの未来　

iPadを眺めると、「それを、歴史はどう判断するのだろう」と思う。スティーブ・ジョブスは、タブレット型のコンピュータ・デバイスについて、今とは違うことを、ずいぶん長い間、言っていたはずだ。技術でなく営業戦略が主の発言だろうから、その一貫性を考えることは無駄なこととしても、iPadが出た今とはずいぶん違うことを、かつては語っていたはずだ。

いくつもの新技術・製品の誕生に関わったジョブスの言葉は、その時代背景・立場に応じて、その内容がずいぶんと変わり続けているように思う。ジョブスが語る言葉はあまり頼りにならないけれど、実際に市場に出てきた製品には、言葉とは違う次元の力がある。

タブレット・デバイスの未来は、どのように私たちの生活の中に溶け込んでいるのだろう。私たちは、それを一体どんな風に使っていくのだろう。そして、新しい製品を選ぶ変わりに、どんなものを私たちは捨てていくのだろう？