hirax.net::inside out::2012年01月

■「未来を想像する力」で「旧暦のお正月」気分を楽しもう!?　

　「こんなものいいな、あったらいいな」と思うものを作りたくなることがあります。作れないことも多いけれど、ごくたまに、欲しいと思った時・その瞬間には「なかったもの」を作り出すことができることもあります。

　そんな時、ほんの少しだけ「未来」を作り出すことができたような、気持ちになります。「こんなものがあったらいいな」という願いは「未来を見て・感じて・味わいたい」という気持ちに似ていて、そして「何かを作り出すこと」は「未来を一部手元に引き寄せる感覚」に、少し似ています。そんな「ほんの少し先の未来」を思い浮かべ・想像し、そしてそこに辿り着くということを、わたしたちはいつも続けているのかもしれません。

　お正月は旧暦に祝いたい、と思うことがあります。旧暦の正月というと、年によって違いはありますが、一月下旬から２月中旬くらいです。日に日に日の出が早くなり、梅の花がもうすぐ咲き始める、そんな頃が旧暦のお正月です。俳句の季語なら一月は「春」の始まりになる、そんなことを実感できる時期です。

　けれど、新暦の１月１日には、そんな「春」を実感するのはまだ少し難しく、まだ寒い冬があって・春はもう少し先のこと…とも思えてしまいます。だから、新春という言葉が交わされる正月は、旧暦でこそ祝いたい、と思ったりします。

　その一方で、「ほんの少し先の未来」を思い浮かべ・想像し、ほんの少し先の未来「旧暦のお正月」までタイムワープをしてみれば、春の風がもうすぐ訪れる・陽気もほのかに香ってくる「、まさに新春」まっさかり…そんな心地にもなってきます。

　2012年、今年の春も間近になりました。さてさて、今年はどんな年になるんでしょう？　今年をどんな年へと、私たちはしていくのでしょうか。

■キッチンでできる「おっぱいの科学」!?　

　豆知識がたくさん詰まった『おっぱい（プリン）食べ終わるまで帰れまテン〜AAAカップからGカップまで…キッチンでできる「おっぱいの科学」!?』です。下の動画は、映画「おっぱいとお月さま」に影響されて作ってしまった（本編とは全く関係ない）予告編です。

■これはビックリ！「手打ち式蕎麦のヒミツ」　

　『これはビックリ！「手打ち式蕎麦のヒミツ」』を書きました。色んなキマリを眺めてみると、意外なくらいに面白い内容が書かれていたりします。…そんなものを眺めたり・楽しんでみたりすることも、昔からハマっている趣味のひとつです。

　さて、ここで問題です。一般的に「手作業で作ってない蕎麦」を、次の中から選びなさい。

1. 手打ち風蕎麦
2. 手打ち蕎麦
3. 手打ち式蕎麦

　さてさて、「○×風」と「○×式」…その違いに思いを馳せるのも、何だか面白いものですね。

■同じバカなら、踊らにゃ損々!?　

　「男の子はバカ。そのまま大きくなるので、オトコという生き物も基本的にバカでヘン。女の子は意地悪。バカと意地悪が共に暮らす人間社会、いろいろあって当たり前」…そんな言葉を読み返すと、「そもそも、意地悪やバカってどういう意味だっけ？」と、根本的なところがわからなくなりました。そこで、辞書をひいてみると、こんな風に書いてあります。

バカ：サンスクリット語 moha の音写。無知の意。愚かな人。道理・常識からはずれている人。用をなさないこと。

意地悪：わざと人を困らせたり、つらく当たったりすること。

　サンスクリット語と言われると、何やら「ありがたいお言葉」のような錯覚すら覚えますが、そのお言葉が言うとおり、「無知」で「愚か」で「道理・常識をわきまえず」「役に立たないこと」ばかりしている自分を（イヤイヤながら）振り返ってみると、少なくとも「オトコという生き物も基本的にバカ」という投票箱に（自分に割り当てられた）一票を（やはりイヤイヤながら）入れざるをえないのかもしれない…という気持ちになってきます（いえ、オトコという生き物も、意地悪な部分をたんまり持ち合わせていると思いもするんですが）。

　オトコはどうせアホでバカ、となれば、「踊るアホウに見るアホウ、同じくバカなら踊らにゃ損々」…そんな声も聞こえてきます。そうはいっても、生まれがラテンな南国からほど遠いせいか、「見るだけのアホ」「勝手なことを呟くだけのおバカなコメンテータ」にもなってしまいがちの自分がいたりもします。

　…というわけで、そんなところを直すこと、つまり、「聞くだけ・見るだけ・言うだけのアホを脱皮して、踊るバカへと変身しよう！」が今年２０１２年の目標です。（アホ・バカという言葉が混在しているので、「バカ・アホ蝸牛考地図」を右に貼り付けてみました。アホもバカもタワケもダラも…色んな踊るアホウがいるものですね）

■コンパクトデジカメを３D深度撮影可能なKINECTモドキにしてみよう!?　

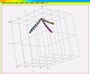
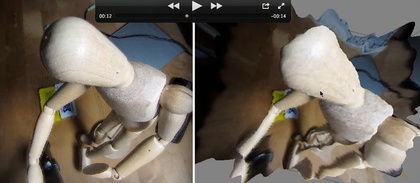　（一万円ちょっとで買った）コンパクト・デジカメを簡易三次元（形状）計測機にしてみました。ピント位置を（輪切り状に）刻々変化させつつ被写体を自動撮影させて、それら（ピント位置が異なる）１７枚ほどの画像群から、３次元形状を再構成してみたのです。再構成した３次元形状をグリグリ回してみたのが下の動画（の右の部分）です。参考までに、撮影した１７枚の画像をパラパラと眺めてみたようすも、立体グリグリ動画の下に貼り付けておきます。

　もう十年近く前になりますが、「ステレオ写真をもとに胸の谷間を三次元的に計測してしまう巨乳ビジョン」や「陰影情報を利用した”巨乳ビジョン Light”」といった「禁断のグッズ」を作ったことがあります。

　今の高機能化が進むデジカメ・スマホカメラであれば、当たり前のように、「リアル”巨乳ビジョン”」機能が搭載されていく…のかもしれません!?

■デジカメの「背面液晶が苦手な理由」と「背面液晶用フードファインダ」　

　背面の液晶画面を見るタイプのデジカメは苦手です。 苦手な理由は大きく分けて、２つあります。１番目の理由は「（比較的一般的な）使いにくさ」の問題で、もうひとつの理由は「個人的な好み」の問題です。

　１番目の理由は「（比較的一般的な）使いにくさ」の問題は、老眼になると近くがみづらいので、デジカメ背面の液晶画面を眺めようとすると「小さく前へならえ」のポーズで眺めざるをえない、という理由です。光学ファインダーであれば、目の老眼に対する補正もファインダ内部で行えるので、「前へならへ」ポーズをする必要がないわけです。

　２番目の「好み」は、個人的な感覚です。「背面の液晶画面を眺める」さまは、「撮影対象に目を向けていない・見ていない」ように感じてしまうという「気持ち」です。光学ファインダーなら、（たとえば）右目でファインダーを介して対象物を見つめ、左目は自分の目から直接対象物を（その周りの広い範囲も含めて）眺めている、と感じられるのですが、「液晶画面」は何か「対象物でない何か他のものを見ている」ように感じられてしまい、気持ちの悪さを感じてしまうのです。これは、本当に個人的な感覚であり好みです。

　ところで、年をとると誰しも老眼になり近くが見えにくくなります。だから、「こういうものがあるべき」という（ローライの）フードファインダー付きデジカメを作っている人もいます。たとえば、右の写真はリコーのデジカメにフードファインダーを取り付けた例です。もちろん、使わない時には折り畳めるようになっていますから、持ち運び時もコンパクトで、とても使い勝手の良い一品です。

　液晶ファインダーを覗くと、たとえば右の写真のような感じです。単に像が拡大されて見やすいというだけでなく、眩しい太陽に照らされた昼光中で撮影する時にも、周りの明るさのために見えにくくなるということもなく、非常に見やすく感じます。

■「ボールペン芯中に空気層が生じる」のは「インク付着力と消費量」が決めている!?　

　ボールペンを使っていると、（たとえば、右の写真のように）芯のインク中に空気が入ってしまい「まだインクがあるのに、字が書けなくなっちゃったよ〜」ということが起きたりします。 ボールペンをシャカシャカと紙の上で走らせてみても、ただペン先のボールが空回りするだけで、紙の上には「何も描かれない」のです。

　ところで、よくよく考えてみれば、この「ボールペン芯の中に空気が入る」という状況はちょっと不思議です。 「インク層に挟まれた透明層は、実は正真正銘”真空”だった！」なんていうことは、あるわけはありません（また、インクの中の何らかの物質が気化したものだ、と考えるのも、組成的に少し不自然です）。インク芯中に、なぜいきなり空気層が生じるのでしょうか？

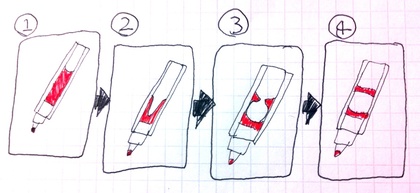　私が考える「発生過程」は右のようになります。 まず、ボールペンを使い、ペン先でインクが使われると、「（右の②のような）ペン芯では外壁にインクが張り付いたまま・中のインクが少なくなった」状態になります。 それは、外から見れば、まるでインクは足りているように見えるけれど、実は中にはインクで無く空気層が押し寄せている、という具合です。 そして、芯外壁に張り付いたままのインクが（いつしか）くっついてしまうことで（③〜④）、最終的に「インク芯中に（あたかも）いきなり空気層が生じたようになる」のではないか、と考えているのです。

　つまり、「インク芯の外壁とインク間の付着力とインクの粘性と、ボールペンの使用状況」にしたがって、「ボールペン芯の中に空気が入る」という現象は生じるのではないか、と思うのです。

　こういった現象は、ボールペンで（急に）たくさんのインクを消費すると、つまり（いきなり）たくさんの文字を書くと生じやすそうな気がします。 インクが急激に消費されると、インク外壁にインクが張り付いたまま、たくさん残りそうに思えます。

　そこで、ためしに、ボールペンでラクガキをひたすらして、１０分あまりでインクを使い果たして見ると、やはり「芯外壁にインクがたくさんへばりついて残ったまま」になりました。 つまり、「ボールペン芯の中に空気が入る」と同じように、「使うことができないインクがたくさん残ってしまった状態」です。 私の経験上は、ボールペンを（いきなり）たくさん使うと、こういった芯外壁にインクが張り付いたままの状態になりやすいように思います。

　ボールペンをよく使う人は、「（自分が）どの程度ボールペンを使うか」という使用頻度と、「インクの粘性・インク・プラスチック間の付着力」を気にしてみると良いかもしれません。そして、「ボールペン芯中に空気層が生じる」過程が果たして（本当のところ）一体どのようなものか調べてみると、面白いかも!?

■「無意味な文章」の見分け方　

　TV・新聞・WEB…全媒体上の「聞く・読む必要が無いコメンテータ」を簡単に見分けようと思うなら、「抜本的な」「明確に」「適正化し」といった「判別キーワード」が含まれていたら、その言葉（を言った人）は右から左に聞き流ししたり・読まずに通り過ぎたり・あるいはゴミ箱に放れば良い、と思っています。
　なぜかといえば、その数文字が持つ「無限の困難さ」を無視した上に構築されたものには、「何の意味も無い」と私は考えているからです。

　そういった「抜本的な」「明確に」「適正化し」といった語句を使うことを躊躇しない「書き手・コメンテータ」は、たいがいの場合、論点先取の誤謬を犯しています。
　つまり、整理してみれば、「○×を止めようとするならば、○×を止めれば良い」といった”堂々巡り”な内容になってしまっているのです。

　ところで、この無意味な文章チェッカーのための重要キーワード「抜本的・明確化・適正化」をGoogleで検索してみると、すなわちググってみると、 go.jp とか （あるいは）各種地方自治体のサイトばかりがたくさん出てきます。その数なんと 28万２千 件です。これは、ある意味見事です。

　 …といった、ことをつぶやいたところ、

　本省の通知に書いてあることを、そのまま自治体の計画で書きますしね。
　また、「できませんよね」と聞き返すと、「だから『～を図る、めざす』と書くんです」という返事がされたりします。それが「言葉遊び」をしているつもりではなく、「使い分けできてる」つもりだから怖い。

と、教えて頂きました。
　”本省通知を自治体計画にコピペする”…なるほど。そういう過程があれば、次々と関連サイトで（そのキーワードが）増殖していきそうですねぇ…。
　そして、”できないことは、「～を図る、めざす」と書く”、そういう”使い分け”がされているとは実に奥が深い、いやむしろ根が深い、というべきでしょうか…。

■「逆に言えば」を使うのはどんなとき？　

　スラッシュドットでこんなコメントを読んで、なぜだか、少しの「ひっかかり」を覚えました。

　「逆に言えば」でちゃんと対偶を持ち出すあなたは結構頭がいい人ですね。大抵は数学的な「逆」や「裏」を持ち出す人が多いので。

　その「ひっかかり」を、自分の中でたぐって考えてみると、まずは「逆に言えば」を使うのはどんなときだろうか？という疑問に繋がっているようです。

　「逆に言えば」という言葉は「”見方”を”逆”にする・ひっくりかえしてみる」というものであって、「（論理学で用いられる）対偶」に相当する文を使うこともあるけれども、むしろ「視点・考え方・発想の転換」を含む（「対偶」というわけではない）文を伴う時こそが、「逆に言えば」が効果的に使われる状況じゃなかろうか…と感じます。そして、それは必ずしも「論理的」というわけでない日常会話中で使われることが多い言葉なのではないか、とも感じたのです。

　その「感じ」を、つまり、

　「（論理学で用いられる）対偶」に相当する文を使うこともあるけれども、むしろ「視点・考え方・発想の転換」を含む（「対偶」というわけではない）文を伴う時こそが、「逆に言えば」が効果的に使われる状況じゃなかろうか？

という「感じ」を整理するために、試しに、「食べた分以上にカロリーを消費すれば太らない」という言葉に続く「逆に言えば」の例を考えてみることにします。

　１番目は、「（論理学で用いられる）対偶」に相当する文が使われる例です。

　消費分より多くのカロリーを取ると、太ってしまう。逆に言えば、太らないということは、消費分より多いカロリーはとっていない、ということだ。

この言葉を聞くと「論理的で仰る通りでございますね…」と思いますが、眼からウロコ的な「転換」といったものは特に感じないのではないでしょうか。つまり、この「対偶」に相当する文例では「逆に言えば」というほどの「逆」感を与えないのです。

　それに対して、２番目のこの例ならどうでしょう。

　消費分より多くのカロリーを取ると、太ってしまう。しかし、逆に言えば、運動を十分するのであれば、いくら食べても良いということなのだ！

　この例では、「（論理学の）対偶」ではなく、むしろ「（論理学の）裏」を感じさせる”流れ”です。その結果、「消費分より多くのカロリーを取ると、太ってしまう」のが正しかったとしても、「運動を十分するのであれば、いくら食べても良い」ということにはならない状況も多々あることでしょう。
　しかし、前半部分の言葉を聞き「食べる量を制限しないとマズイかな…」という雰囲気を感じた相手に、「食べる量じゃないんだ！どれだけ運動するかなんだ！」と力一杯叫ぶ熱血体育会的な「視点・考え方・発想の転換」を感じさせるのではないかとも思います。

　論理的に正しい・正しくないではなく、「視点・考え方・発想の転換」があり、それが何らかの眼からウロコ的な気づきを与える言葉の前にこそ置かれるべきなのが、「逆に言えば」ではないか、と想像したのです。

　冒頭の「ひっかかり」は、こう言い換えても良いのかもしれません。

　演繹的に正しい言葉、論理的に１００％正しい言葉を使うのは、果たして”頭がいい人”なんだろうか？

　「視点・考え方・発想の転換」を伴わなければ、進歩もないし・新しい何かが生まれることもないし・楽しくもないんのではなかろうか…というようなことを（非論理きわまりないアタマであるせいか）感じた…ということになります。

■Wolfram Mathematica とCDF Playerの違いを図解してみた　

　Mathematica研究会で、Wolfram CDF Playerでローカルデータを読み込むというネタを聴きました。 Wolfram CDF Player というのは、数式処理ソフトウェアであるWolfram Mathematicaで作られたファイルを「閲覧・再生」するためのソフトウェアです。 しかし、実際のところ、Wolfram CDF Player は制限が付けられたWolfram Mathematicaというようなものなのです。 そのため、前述のような「Wolfram CDF Playerでできることの限界を試そう」という技術的な試みがされたりします。 そこで、Wolfram CDF Playerの制限について、（現時点での）頭の整理がてらラクガキしてみました。

　CDF Player(以前の名前であるMathematica Playerもほぼ同様)は、Mathematicaで作成されたCDFファイルしか開けず（ファイル内容と作成元Mathematicaのライセンス番号から定まる”だろう”チェックサム確認を行います）、ユーザ入力が「数値のみ」・ローカルファイルパスからのImportができない、といった制限がかけられています。

　そこで、Wolfram CDF Player( 計算コアであるMathKernel)を使い切るために、図中に青数字で描いたような経路を使い、色々な「汎用化」がされています。つまり、

1. Mathlink経由でMathKernelを直接叩く（「無料配布のMathematicaカーネルをIronRubyから自由自在に使ってみよう」など）
2. 任意のコード・データを数値エンコードして、Imputフォーム経由で突っ込む（「Universal Mathematica Manipulator—Poor Man’s Mathematica」）
3. ローカルファイルパスでなく、ネットパス経由のImportを行い、コード・データを突っ込む（「Wolfram CDF PlayerをMathematicaとして使う方法」）
4. J/Link（MathLink経由Javaインターフェース）でコード・データを突っ込む（「Wolfram CDF Player を汎用する」など）

といった「道・やり方」が（技術興味から）踏破されてきた、という具合です。

　２番目の手法は「コードもデータも区別する必要なんかないね！」という思想が見え隠れしますし、３番目の手法は「ネット経由でのデータアクセスはできるだろうし、そうならば（やろうと思えばDNS偽装でも何でも）後はいくらでもやりようがある」という技術的な読みが感じられて、それぞれの技術的な趣きがあり、なかなか面白いものです。

　Mathlinkからの接続がCDF Playerのカーネルでも有効になっているのは（Mathematica本来の動作構造と直結しているため）単純に機能を止めてしまう・壁を作ってしまうわけにはいかないという辺りだろうか、と想像しています。 また、ネットパス経由のImport機能が有効なのは、データ・アクセスのために必要で、その機能を止めるわけにはいかない（機能を止めてしまうと魅力的なデモが大幅にできなくなってしまう）、という辺りの理由を疑っています。 …というわけで、今日は、自分用のメモ・ラクガキをしてみました。

■（冷めた）USBあったかアイウォーマー２を「熱いヤツ」にしてやるぜ！　

　USBポートに繋げば「目の上に乗せれば、蒸しタオルを乗せた時と同じように気持ち良くなる」という売り文句のサンコー「USBあったかアイウォーマー２」を、疲れ目対策のために買ってみました。

　しかし、使ってみた感想は、「（スイッチを入れたはずなのだから）暖かくなってるはずだよな？かすかに暖かくなってるかな？むしろ全く暖かくないような…」？という具合で、心頭滅却して精神集中しないと、暖まっているのすらわからない程度です。つまり、ほぼ暖まらないのです。

　そこで、このほとんど暖まらないサンコー「USBあったかアイウォーマー２」を、適度に熱くなるように改造してみることにしました。

　まずは、ハサミで端っこを切り開きます。そして、中身を確認してみると、発熱線を適度に這い回した発熱シートが入っています。 発熱シートの電気抵抗を計ってみると、ほぼ１０Ωです。 つまり、USBの最大供給電力2.5W（=5V×5V/10Ω）をピッタリ使い切る設定です。

　ちなみに、発熱の程度を変化させる強弱スイッチがありますが、これは「弱」の時には抵抗がはさまることで、発熱体への分配電圧が2.5V程度になるというだけのものです。ですから、機器としての消費電力が変わるわけではありません。

　消費電力といえば、この「USBあったかアイウォーマー２」の加熱能力は、USB給電の定格である2.5W=毎秒0.6カロリー弱を発生させることができる、というだけのものです。ということは、100ccの水の温度を20℃上げるにすら１時間かかっても難しそう…という程度です。

　そこで、手持ちのACアダプタを「サンコーのUSBあったかアイウォーマー２」に繋いで、10V弱を給電してみました。つまり、定格の４倍近い10ワットの電力で発熱させてみたのです。クールでニヒルで冷めたいUSBあったかアイウォーマー２を熱いヤツにしてやる！というわけです。　

　この（通常比３倍の”赤い彗星”をも上回る）４倍ブーストモードにしてやると、発熱体はあっという間に暖かくなっていきます。そして、６０秒もしないうちに７０℃近くに達しました。･･･これなら、アチアチなスチームタオルの代わりの「アイウォーマー」として使うことができそうです。

■昔の横浜・東京がいつも夜霧に包まれていた「理由」とは？　

　 「学生の可能性を可能にするポータルサイト ワンダーノーツ（Wonder Notes）」に「昔の横浜・東京がいつも夜霧に包まれていた「理由」とは？」を書きました。

　最後に書いたのは「どんな時代に生まれたいですか？」という「質問」です。…誰も「どんな時代に生まれるか」を選ぶことはできないのですけれど、ね。

　何十年も前、横浜や東京という街は、一年のうちのかなりの日数「霧」に覆われていました。 夜になると白い霧が、時に不気味に、あるいは、時にロマチックに街を覆い出す…横浜や東京という街は、そんな場所でした。 だから、昔の懐メロ（懐かしのメロディ）には「夜霧よ今夜も有難う」「東京夜霧」「夜霧の第二国道」といった、タイトルの歌が、多く残っています。 けれど、そんな「霧に覆われた街」を、最近は想像することが難しくなってしまいました。

　東京や横浜の街を霧が頻繁に覆っていた昔の時代…東京や横浜から霧が消えてしまった今の時代…あなたは、どちらの街を生きたいと思いますか。どちらの時代が好きですか？

■「高校・大学の頃の自分」に送る「短く具体的なメッセージ」　

　Shiroさんの「知的なツール、努力の方法」から、"I'm not as smart as I thought I was. "（日本語訳：僕は自分が思っていたほどは頭がよくなかった）を読んだ。

　悩む高校生に対して返されたMIT卒業生によるアドバイスを、高校生だった頃の自分が読んだとしたら、間違いなく「どうすればいいのか、全然わかんないよ…」と思うだろう。 「…意味分からないし。もっと、短くて・具体的に何を・どうやればいいか教えてくれよ」と感じるに違いない。 あるいは、「高校の卒業生総代に選ばれなかった」とか「MITに行けなさそうだ」という（天上界の）高校生の悩みに対して、「頭のいいヤツはこれだからよー」と斜に構えたコトを考えるだけかもしれない。

　「MIT卒業生によるアドバイス」は昔の自分には絶対に届かない。 だから、高校生だった頃の、そして大学生になった頃の（他の誰でもない）自分自身に向けて、短く・具体的なメッセージを書いてみることにした。 そのメッセージは、たった２つだけだ。

　１番目のメッセージは、世界（つまり、自分の先にある未来）は「わからない」ものがたくさんある、ということだ。 だから、「ぼくの頭ではわからない…」と感じ、自信を失い・不安になるような状況は、もう数え切れないくらい何度も何度も繰り返し訪れ続ける、ということだ。 それまでに獲得した「（特定の）力・道具」だけでは、乗り切れそうにないように思えるかもしれない時が、それはもう何度も訪れる。 …そんな状況や不安と折り合いをつけ・それに負けずに共存していくために必要な「方法・能力」について書いたのが、次のメッセージだ。

　２番目のメッセージ、それは「好奇心・興味」を持ち、「未来・可能性・したいこと」を想像し・見つけ出す心を持て、ということだ。 それが、どんなにくだらなく思えることでも、何か「自分が楽しくなる・それをやりたくなる・そこまで辿り着きたくなる」ものを夢見て・焦がれる心を大切にしろ、ということだ。 「好奇心・興味」や「未来・可能性・したいことを想像し・見つけ出す気持ち」が大切でとても有効だということを、その証明を次に書く。

　「手に入れる結果」というものは、どうやら「努力した量」と（やはり）「天性の力」が掛け合わされたものと一致するようだ。 それは、つまりこんな方程式だ。

手に入る結果 ＝ 天性の力 × 努力した量

多少の誤差はあるようだが、この方程式は結構正確だ。 「手に入れる結果」に「天性の力」は関係ないと言ってしまえば、多分それはウソだ。 きっと、それは間違っている。 「手に入れる結果」は「努力した量」でも決まるが、「天性の力」にも比例する。 同じ時間努力しても「手に入る結果」は人それぞれ違う。 そこには確かに「天性の力」が関係している。

　「天性の力」を意志で変えることができないのであれば、その分「努力する量」を増やせばいいという言い分は多分真実に近いのだろうと思う。 …しかし、「努力する量」をただ増やせばいいなんていうメッセージを他ならぬ君に送るつもりは全くない。 それでは、ただの精神論で、その精神論を実践する根性も忍耐力も、残念ながら君は天性持ち合わせていないということを、（君と同じ本人である）私が一番よく知っているからだ。

　重要なヒントは、上に書いた方程式だ。 この方程式は、「右辺が左辺を決める」と読めるかもしれないが、それと同時に「左辺が右辺を決める」とも読むことができる。

努力する量 = 手に入る(だろう)結果 ／ 天性の力

この方程式に登場する「定数」は、実は「天性の力」だけだ。 「手に入れる（だろう）結果」と「努力した（する）量」は、それは間違いなく「変数」だ。 「努力した量」で「手に入れる結果」が決まるとも言えるが、それとは逆に、「手に入れる（だろう）結果」次第で「努力する（できる）量」が決まる、とも言える。 つまり、「手に入れる（だろう）結果」を、豊かな想像力・妄想力で描いて・それを欲すれば、「努力する量」はいくらでも増える、ということだ。

　「天性の力」を増やすことができなくても、「手に入れる結果」…その楽しさ・面白さを想像し拡大することは、無限にできるはずだ。 タダなのに無限に使うことができるという存在、それが想像力だ。

　努力した量が手に入る未来を決めるんじゃない、無限の好奇心・興味・未来や可能性を想像して見つけ出す心・自分が楽しくなる何かを見つけ辿り着きたいと欲する心…それが、「無意識のうちに努力する量」を限りなく増やし、そして未来を作り出していくんだ。 だから、世界を見て・未来を想像して・くだらない好奇心やささいな興味を大切に持ち続けて欲しい。 それらは、不確実で・わからないことばかりで・変化し続ける世界の中でも、いつだって、その先へゆっくりと歩き続けようとする「原動力」になるはずだ。

　さて、こんなメッセージを（年の離れた）君に送った理由は、もうバレているに違いない。 つまりは、２１世紀ののび太（の子孫）が２０世紀にドラえもんを送った理由と同じようなものだ。 21世紀を歩く未来の僕を作り出すだろう20世紀にいる君が、「夢を見て・何かを手に入れたいと思う欲望・気持ち」を少しでも増やしてくれるといいなと…君の未来は他（？）力本願に願っているわけだ。

　未来を作る「原動力」は、未来に対する無限の欲望や想像力だ。 未来を夢見て、自由自在に描き出し、そこへ辿り着きたいと願う力を、大事に抱えて続けて欲しい。

■ゲーテが「囲碁の碁石の大きさ」を予言していた？　

　 「学生の可能性を可能にするポータルサイト ワンダーノーツ（Wonder Notes）」に「ゲーテが「囲碁の碁石の大きさ」を予言していた？」を書きました。

　囲碁で使われる碁石、白石と黒石の大きさは、同じではありません。実は違うサイズなのです。…なぜ、囲碁で使われる碁石は、白石より黒石の方が大きいのでしょうか？

　ちなみに、ゲーテがの「色彩論」は、描かれた「イラスト」の美しさに驚きます。イラストレータとしても、ゲーテは超一流だったのです。

■「自分自身」に向けた「メッセージ」　

　最近の「とりとめもない、つぶやき（twitter）」から。

　努力した量が手に入れる未来を決めるんじゃない。無限の好奇心・興味・未来や可能性を想像して見つけ出す心・自分が楽しくなる何かを見つけ辿り着きたいと欲する心…それが、「無意識のうちに努力する量」を限りなく増やし、未来を作り出していくんだ。

　「苦労や悩み」は「必然」で、それを減らすことも消し去ることもできないけれど、「そんなものを無視できるくらいの魅力」を「見つけ出す・欲する」ことはいくらでもできるはず…それが「未来」というものじゃないか…と。うーん、何だか小さな赤ちゃんを（想像できないくらいの）痛みを伴って産み、そして、育てるお母さんにとっての「可愛いベイビー」みたいだ。

　「運」や「偶然」は、未来を決める大きな要素だと、確かに思う。…その上で「（天性でない部分の）才能」や「（なにがしかの）運」といったものには、「それらを生み出す”何か”」「自分が操作することができる何か」も、人それぞれ違うにせよ、存在しているんじゃないかとも思う。…いや、「思う」と決めている（そう思わないとやってられないから）。

　先日、隣の楽屋に「中林鉄太郎 様」と貼られていて驚いた。驚いた理由は、そのほんの少し前、中林・安西両氏らのローカリゼーションマップに興味を持ち、お二方のお話を聴きに伺ったばかりだったからだ。そして、それから数週間も経たないうちに、思いもがけない場所で隣り合わせる偶然に驚いたのだ。…これは確かに「偶然」だ。けれど「（ローカリゼーションというものに）興味を持つ」「そして、中林・安西両氏に話を聴きに行った」ことがあって、ようやく生じる偶然なのだ。そういう「偶然」は、結構ある。

　右辺と左辺、どちらかが原因でどちらかが未来だと決まっているわけじゃない…と思うことが大事だ。右辺と左辺を自由自在に動かす想像力と機転を、必ず手に入れて欲しい。

　『「高校・大学の頃の自分」に送る「短く具体的なメッセージ」』で書いた言葉を、さらに短く「ひとこと」にしてしまえば、「大変なこともある。それでも、未来に魅力を感じる力を手に入れて、前に進み続けろよ」ってことなんだろう。過去・現在（それはまさに自分自身だ！）・そして将来…すべての・ありとあらゆる自分自身に向けて。

■エラー・ダイアログを吐いて休憩中の「公共システム」たち　

　PCが不調になり、意味不明の言葉が貼り付けられた「ダイアログ」を表示したまま、そのまま動かなくなってしまうことがよくあるものです。こういった「ダイアログ」を吐いたままシステムが「動かなくなる」のは、決して手元のPCだけ、というわけではありません。

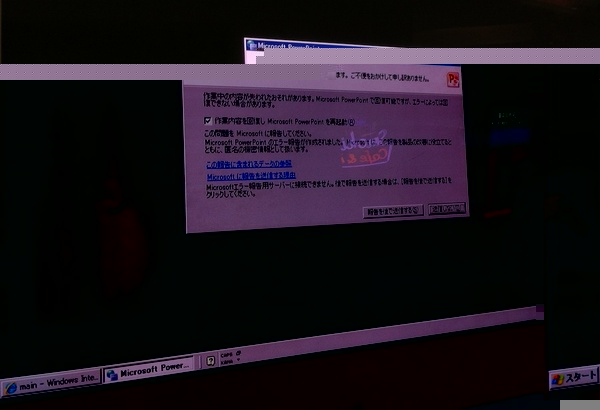　羽田空港の一角で、壁に埋め込まれた巨大ディスプレイに「問題が生じたためPower Pointが終了しました」というダイアログが出ていました。

　「珍しいこともあるものだ」と思ったのも束（つか）の間、よくよく周りを眺めてみれば「ダイアログを画面中央に”出現”させ停止しているディスプレイ」が結構あることに気づかされます。

　たとえば、「両替レート」を映し出しているかに見えて実はエラーダイアログを表示したままの巨大ディスプレイ、そしてその近くではJavaアップデート関連のエラーダイアログを映し出している空港内の両替コーナーディスプレイ、HTTPエラー500番を表示したままのキャッシュディスペンサー、Windowsメッセンジャー関連のエラーを吐いたままウンともスンとも言わずに眠っている空港情報システム…。

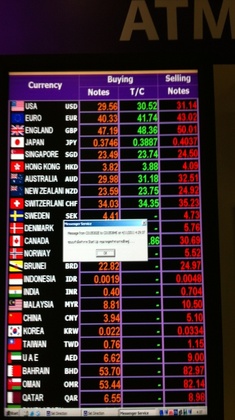
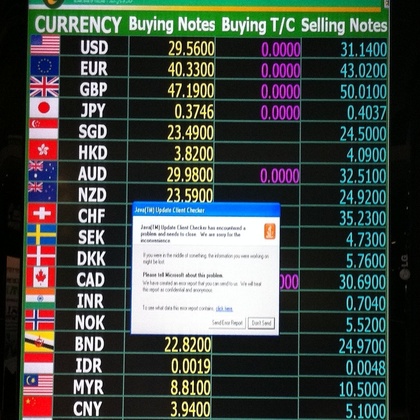
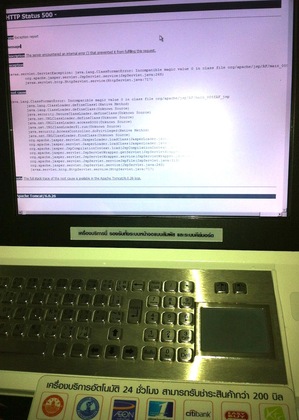
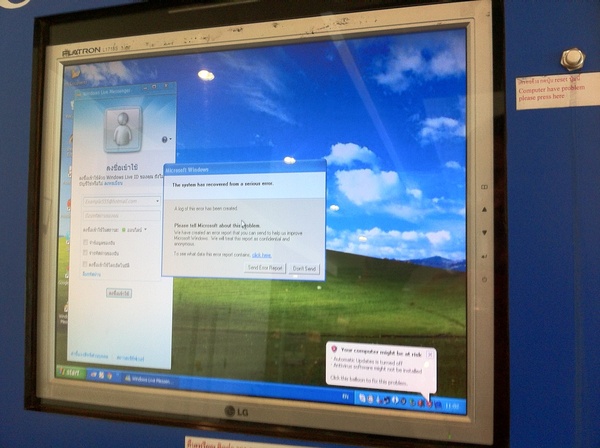
　２４時間、休むこと無く働いているように見える公共システムも、よくよく眺めてみれば…実はスヤスヤ眠っていたりもするのです。働くばかりでなく・一休みしている「機械」を見ると、何だか人よりも人らしい、逆に言えば、人が機械より人らしくない、そんなように思えてきたりもするのです。

■2011年にAmazon広告経由で販売された「トップ１０」(hirax.net調べ)　

　「色んな商品の値段を調べてみよう！」と思い立ちました。 値段調査をしてみたい！と思い立った理由（とある調査・研究をしてみたかったのです）は明日にでも書きますが…「商品の値段一覧」を手に入れるためにはどうすればいいだろう？と考え込みました。 商品価格一覧なんてどこにでも転がっているようにも思えますが、よくよく考えてみると、あまり眺めたことがないように思います。 …頭をフリフリ考えて、思いついた「策」が（hirax.netに貼り付けられている）Amazon広告経由の商品販売データを使おう、ということでした。

　そこで、さっそく「2011年にAmazon広告経由で販売された商品データ一覧」をダウンロードして、いくつか解析をしてみました。 まずは、hirax.netの広告経由で2011年にAmazon広告経由で販売された「トップ１０」を下に貼り付けてみます。

　2011年晴れて「No.1]に輝いたトップ・セラーは「IR 86 7.5X1 光吸収・赤外線透過フィルター」です。2011年の1〜12月の間に（多いのか少ないのか）62枚ほど売れています。自分の本（論理的にプレゼンする技術）より、やっぱり赤外線透過フィルターの方が売れるんだなぁ…とか、それでもTENGA より上にあってくれて（なんだか）良かった…とか、実に趣深い2011年の「ベスト１０」です。

1. IR 86 7.5X1 光吸収・赤外線透過フィルター(IR)
2. 論理的にプレゼンする技術〜聴き手の記憶に残る話し方の極意
3. 原子力防災―原子力リスクすべてと正しく向き合うために
4. 酔いがさめたら、うちに帰ろう。
5. 男たちへ―フツウの男をフツウでない男にするための54章
6. おとなの小論文教室。
7. レノボ・ジャパン ThinkPad X100e Slingケース
8. 文章読本
9. TENGA エッグシックスカラーズ パッケージ
10. 新 物理の散歩道〈第1集〉

　というわけで（気を取り直し）、商品の価格一覧を調べた「本題の実験・調査」については、明日書いてみることにします。

■実証データと共に眺める「ケータイと電卓の数字ボタン配置が異なる理由」　

　　 「学生の可能性を可能にするポータルサイト ワンダーノーツ（Wonder Notes）」に「ケータイと電卓の数字ボタン配置が異なる理由」を書きました。

　「ケータイや電話機」と「電卓」は、どちらも数字が同じように並んでいる…ように見えて、実は「数字ボタンの並び方」は違っています。 たとえば、ケータイと電卓を机の上に並べてみれば、ケータイなら「小さな数字のボタンが遠くにある」のに、電卓では「小さい数字」は手元＝近い方にあります。 つまり、ケータイや電話機と電卓では、ボタンの位置が実は「逆」になっているのです。 それだけでなく、電話機の「０」は「９」の近くにありますが、電卓の「０」は「１」の近くにあります。

　…というわけで、今日は『ケータイと電卓の数字ボタン配置が異なる理由」を、「あぁ、なるほど」と納得・実感できそうなデータとともに、ご紹介してみました。

　ちなみに、この記事中で使った「データ」は「2011年にhirax.netにAmazon広告経由で販売された商品一覧」です。

　参考までに、「商品の値段の一桁目の数字は何か？」を調べてみた結果は、右のグラフです。（ある条件下においては）「一桁目の数字の３割は”１”にある」という「ベンフォードの法則」に沿っていることがわかります。

■続々？Mathematica機能を使うIronRubyコードを書いてみる　

　数式処理ソフトであるMathematicaの機能をIronRuby(.NetによるRuby実装)から使うRubyコードを少し書き直してみました（mathruby.rb）。具体的には、Mathematicaの計算カーネルと「やりとり」をする通訳部分に、Mathematicaから得られた値をRuby側のクラス（Array,String,Numeric 等）に自動変換するコードを付け足してみました。

　このRubyスクリプトを実行するディレクトリに"Wolfram.NETLink.dll"（ここからダウンロードできるファイルを展開した中にあります）を放り込んで、たとえばこんな「２次方程式の解を求めよ」というコードを書くと、そして、そのRubyスクリプトをIronRubyから実行すると、

pp 'x^2 == 3'.Solve 'x'

次のように答が得られます。

[["x -> -Sqrt[3]"], ["x -> Sqrt[3]"]]

Mathematicaの計算カーネルからRubyが得る答は、もちろんRubyのArrayクラスのオブジェクトです。２次方程式の解ですから、要素が２個の配列が返されています。

　あるいは、 pp [1,2,3].Sin.N というコード、つまり、配列[1,2,3]のそれぞれに「Sin関数を適用した上で、”数値化”せよ」という命令を書けば、

[0.841470984807897, 0.909297426825682, 0.141120008059867]

という「数値」クラスのArray（配列）が得られます。

　違う言語の間を「繋ぎ」を作ろうとすると、それぞれの特徴（売り）・個性・違いを（ほんの少しだけ）垣間見ることができるような気がして、何だか少し面白いもののです。

---

　上記コードの動作確認は、Windows上で行っています。.Net実装であるmonoを動かしたOSX では、monoの正規表現動作不具合などにより、上記コードは動作しません(2012/01/28現在)。

■アメコミ・ヒーローの「色使いのヒミツ」を調査せよ！　

「学生の可能性を可能にするポータルサイト ワンダーノーツ（Wonder Notes）」に「アメコミ・ヒーローの「色使いのヒミツ」を調査せよ！」を書きました。記事後半で紹介した「色指定用のカラー・チャート」や「スーパーマンの色付け作業原稿」は、意外に面白く・興味深く感じられるのではないか、と思います。

右に貼り付けたのが、かつて使われていた「６４色のカラーチャート」です。色あせ・変色してしまっていますが、この６４色がアメコミの主要登場人物たちを特徴付けていた、ヒーローたちを彩り・作り上げた基本色なのです。

■「貿易赤字額」と「原油価格推移」をグラフにして眺めてみよう!?　

　「貿易赤字」についてのニュースや記事を見ても、なかなか意味がわからなかったりします。そんな時、「ことばだけの説明」や「短いコメント」では何がなんだかわからないよなあ…と考えます。

　そこで、「貿易赤字」について「学んでみよう！」と思い、まずは財務省貿易統計ページから貿易収支のデータを取得して、輸入額・輸出額の推移をグラフにしてみました。

　なるほど、確かに輸入額が輸出額を超えています。しかし去年がどうというよりは、ここ何年もの間「輸出が停滞している」ようにも見えます。また、リーマンショック前後など、それとは異なる、遙かに大きな動きも実感することができます。

　さて、次は、輸入金額の内訳（財務省貿易統計）を項目に分けてグラフにしてみることにします。

　すると、原油と石油製品が卓越していることがわかります。しかし、その動きは、去年１年の間の動き（震災の影響）より、もっと違う「動き」の方が大きな影響を与えているようにも感じられてきます。

　そこで、さらに原油価格の動きもグラフにしてみました。それが、下のグラフです。

　原油輸入量（金額）＝数量（輸入量）＋単価（原油価格）ということになるのでしょうが、原油入金額の推移に関しては（輸入量）よりも、原油価格の「揺れ動き」の方が遙かに大きく卓越しているように見えて・感じられてきます。

　少なくとも、「短いことばによる説明」では何も実感できないことであっても、「眺めてみる」ことで自分なりに何かわかったり・感じたりすることができるものです。…というわけで、今日は「貿易赤字額」と「原油価格推移」をグラフにして眺めてみました。

---

参考：2011年の石油と石油製品の輸入（数量、平均単価との関係）
参考：2009～2011年の化石燃料の輸入（輸入量と輸入額）

■「Mathematicaの色（スペクトル計算）関数」手直し版　

　Mathematicaで色（スペクトル）計算をしたり、計算結果を表示するのに便利な関数を（ほんの少しだけ）作り直しました（ColorImagingFunctions.txt）。CMYKの画像ファイルを開き、「画像のこの辺りのピクセルは、一体どんな色（スペクトル）になるんだろう？」なんていう計算をする時の「叩き台」になるかもしれない（ならないかもしれない）という、そんな関数群です。

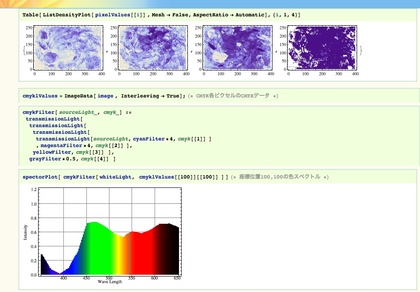
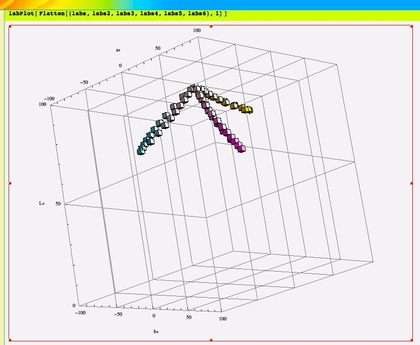　たとえば、右に貼り付けた画像は「典型的なカラーインクの吸収スペクトル（シアン・マゼンタ・イエロー）で面積階調・濃度階調を表現した際の色変化を示したグラフです。こういった処理を下記のようなコードを書くことで行うことができる、そんな関数群を書き直してみました。

labs = Map[lab, 
  Table[transmissionLight[D65, 
   cyanFilter, d], {d, 0, 4, 0.4}]]
labPlot[ labs ]

■C++の「i++ と ++i の違い」とExcelの「i++ と ++i の違い」　

　ビール瓶を開けながら「プログラミング言語」の話題をしました。プログラミング…と言っても、思い切り（プログラミング言語的には）低レベルな話ばかりです。ここで言う「低レベル」というのは、ハードウェアに近いとかそういう意味の「低レベル」ではありません。

　たとえば、「C++で書くけど、ほぼFORTRANなんだよね〜」という「一体どんなC++だぁ？」というツッコミをしたくなるコード論であったり、「それって、必ず７文字のインデントを入れてからC++のコードを書くってことですか？」というこれまた低次元な「インデント論」だったりしたのです。

　そんな中、「（C++なら）とりあえず、a++とは書かずに、++aと書きますよね」という話になりました(参考：C++のi++ と ++i の違い)。そして、さらに、「（C++ではなくて）C言語のi++ と ++i の違い」みたいなことをMicrosoft Excelでも気にすることがあるか？という話題になりました。話題が脈絡無くサブルーチンに"GOTO"するのは、それは単にアルコール１００％の酔っぱらいだから、です。

　「C言語のi++ と ++i の違い」みたいなことがMicrosoft Excelでもあるか？気にするか？というと、その答えはもちろん「YES」です。…なぜかといえば、たとえば、A1,B1,C1という３つのセルがあった時、それらの各セルに対して、
A1=B1
B1=B1+1
C1=B1
という式を設定する場合など、（自分自身のセルを参照する）循環参照になっているために、その際の計算順序は単純にZの法則にしたがって左→右・上→下の順番で行われるために、計算結果は
　A1,B1,C1=1,2,2
となるからです。A1とC1は、同じ式がセルに入力されていても、実は違う値（タイミング）のB1を参照するがために、違う値になるのです。…それは少しばかり「（C言語の）++iとi++の違い」に似ています。

　C++という言語名は「C＋＋って、（＋＋Cじゃないから）使う時は（前の値と同じというわけで）Cに過ぎないよね？」といった冗談をよく聞いたような気がします。それぞれの言語が抱える「（ちょっと意外にも感じる）++iとi++の違い」にはどんなものがあるのでしょうか？そしてまた、Microsoft Excel で++aとa++の違いを気にする人は、一体どのくらいいるものでしょうか？

---

参考：AWKの場合

■（ヤング率的に）かなりヤングな「おっぱい断面方程式」　

　美しい景色を見ると心動かされるように、美しい方程式を見ると感動します。そして、その方程式を見い出した人が持つ「力」に涙するものです。

　今日は、「おっぱい断面方程式発見」というニュースに心動かされました。

@Xe_no: おっぱい断面方程式：x=3 y log[y]-1/36 exp[-(36y-36/e)^4] ( 0≦ y ≦1 )

　もちろん、単に心動かされるだけでなく、自分でも「おっぱい断面方程式」をなぞってみたくなり、喜び勇んで？グラフにしてみました。それが、右に貼り付けたグラフです。

　これは、「オッパイ古典力学研究者」としての感覚的には、そして力学的・ヤング率的には、「かなりヤングな断面」に思われます。

　「おっぱい（曲面）方程式」とか、「美的曲線」基準の「理想バスト形状」とか、「オッパイ水風船曲線」とか、美しい方程式を求める努力は実に涙ぐましいものですよね…oπ。

---

参考：Wolfram Alpha版