2012-04-01[n年前へ]
■iPhone 5の目玉機能「画像認識エージェント”ハピネス”」は四つ葉のクローバを見つけ出す！ 
『iPhone 5の目玉機能「画像認識エージェント”ハピネス”」は四つ葉のクローバを見つけ出す！（期間限定公開）』
今年の後半に発売される予定のiPhone 5 には、画像認識エージェント 「ハピネス “Happiness”」 が搭載されます。 その画像認識エージェント「ハピネス」は、「（言葉にできない）人が見つけられないもの・けれど人が求めているものを、iPhone が見つけ出す」という機能です。
現行機種 iPhone 4s の目玉機能は、音声認識エージェント Siri でした。 Siriを使えば、音声を認識して、音声に応じて適切な処理・作業をしてくれます。 「やって欲しいこと」をiPhoneに言うだけで、音声認識エージェントSiriは色々なことをしてくれます。 しかし、Apple によれば「（意外なことだが）”やりたいこと”を自分自身では見つけられない・言葉にできないユーザが少なからずいる」というのです。この「（意外なことだが）”やりたいこと”を自分自身では見つけられない・言葉にできないユーザが少なからずいる」というApple関係者の言葉は、”ユーザ”だけでなく、”他メーカ”に対しても向けられているのではないか、と（気のせいかもしれませんが）感じました。
2012-04-02[n年前へ]
■「ウォーリーを探し出す」Mathematicaコードが「してること」
「Mathematicaでウォーリーを探せ！」（"How do I find Waldo with Mathematica?"）が面白かったので、Mathematicaのコードが何をしているかを眺めてみました。
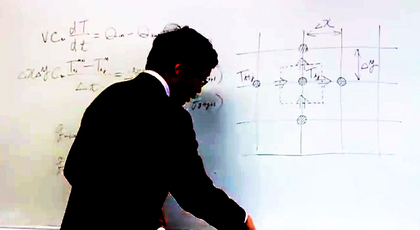
まずは、Mathematicaコードに簡単な注釈を書き加えてみました。それが下のラクガキです（エッジ検出のテンプレートを間違って4x5で描いてしまいました。正しくは4x4です）。
このMathematicaコードは、次のような処理を行います。ウォーリーを見つけるために用いられているのは、「（赤色に対する）横エッジ検出」です。
- 所定のURLから現画像(waldo)を読み込む（Import)
- 現画像(waldo)をRGBそれぞれの画像として分解
- RGB画像から（R-G-B)という演算を行い、赤色の量を示す赤画像（マトリクス）を作成
- 横（水平）エッジ検出用テンプレート（4x4）を作成。テンプレートは上半分＝１、下半分＝０
- 赤画像の各領域と横（水平）エッジ検出用テンプレート間で”相関”（実際にはベクトル間距離）を算出
- ”相関”画像を閾値をもとに２値化
- ”相関”画像は実際には”距離”を使っているので、「値が小さい方がマッチしている」ので、値を反転(ColorNegate）
- 膨張処理用に円形のカーネルを作成(DiskMatrix)
- ２値化された（マッチするほど値が大きい）”相関”画像を円形カーネルを使って膨張処理（Dilation）
- 非マッチ部は0.5・マッチ部は1.0にサチらせたマスク画像作成（ImageAdd部）
- 原画像（waldo）とマスク画像を乗算し、完成！
ウォーリーを見つけ出すために使われた③④⑤あたりの「（赤色に対する）横エッジ検出」処理が、シンプルだけれどもなかなか上手く動いているようで、とても面白く感じられます。エッジ検出用のテンプレートのサイズも、4x4という大きさは「必要十分」で上手い…と感心させられます。
ところで、このMathematicaコードでは、「赤白の横線部があると、ウォリーでなくともマッチしてしまう」でしょう。もしも、より確実にウォーリーだけを見つけ出そうとしたら、一体どんなコードを書けば良いのでしょうか？（この続きが『「ウォーリーを探す出す」多重解像度解析コードを書いてみる!?』です）
2012-04-03[n年前へ]
■「ウォーリーを探す出す」多重解像度解析コードを書いてみる!?
「ウォーリーを探し出す」Mathematica コードがとても面白く・参考になりました。そして、もしも「ウォーリーを探し出す」コードを書こうとしたならば、自分ならどんな風に書くだろう？と考えました。…そこで、試しに、書いてみることにしました。
まずは、画像を読み込みます。
waldo=Import["hoge"]そして、ウォーリーを見つけるには、「やはり、赤白シャツを頼りにすべし」というわけで、赤白模様を検出するための単チャンネルを作成します。ここで、2{1,-1,-1}.#&は、R-G-Bを計算する純（無名）関数です（Stack Over Flow のコードと同処理です。カスタマイズできるように純関数にしています）。
red=ImageApply[2{1,-1,-1}.#&,waldo]次は、ウォーリーを探す部分です。Stack Over Flow で書かれていたコードは「横方向の赤白線の上エッジ検出」を行い、「強いエッジがある部分にウォーリーがいる」という推定を行います。
しかし、その推定では、「ウォーリーが着ているシャツは、赤白横線が何本も入っている」とか「その赤白横線は、胴の形に添った形状をしている」といった情報は用いられていません。
そこで、「胴の形をした赤白横線模様」を作り、さらにその「模様」を用いた多重解像度解析（ウォーリーの大きさは未知ですから）をすることによりウォーリーの位置を推定する、というコードを書いてみました。
mask=Fold[ImageAdd,#[[1]],Rest[#]]&@Table[このコードでは、多重解像度解析を行った上で、ありとあらゆる解像度、すなわち、ありとあらゆる大きさのウォーリーがいる（だろう）位置を、一枚のマスク画像へと焼き付けます。
h=a;w=Floor[h/2];
corr = ImageApply[ 4 Abs[# - .5] &,
ImageCorrelate[red,
Image@ Table[Cos@y, {y, 1, 6 Pi, 6 Pi/h}, {h}],
NormalizedSquaredEuclideanDistance ]];
ImageApply[ #/(30 - 5) &,
Dilation[ImageApply[ If[# > .8, 1, 0] &, corr],
ConstantArray[1, 4 {h, w}]] ] , {a, 5, 30}]
そして、焼き付けた（推定した）「ウォーリーが立っている位置のマスク画像」を用いて、原画像からウォーリーを浮き上がらせてみます。それが、以下の（Stack Over Flowそのままの）最後のコードです。
ImageMultiply[waldo,
ImageAdd[ColorConvert[mask, "GrayLevel"], .5]]
試しに、「ウォーリーをさがすとはどういうことか」で使われていたサンプル画像に処理をかけてみると、次のようになります。これが、「ウォーリーを探す出す」多重解像度解析コードです!?
赤白模様の「壁」などにマッチしないようにしたい場合のために、下記のようなフィルタリングを加えると良いかもしれません（今回はコードを短くするために割愛しました）。
corr2 = ImageApply[ 4 Abs[# - .5] &,
ImageCorrelate[corr,
Image@ Table[
If[x^2 + y^2 < h, 1, 0], {y, -h, h}, {x, -h, h}],
NormalizedSquaredEuclideanDistance ] ];
2012-04-05[n年前へ]
■ポケットガイガーで「土サンプル」を計ってみる
久しぶりに（フリスクケースに入った空間線量計である）ポケットガイガーを取り出して、「土サンプル」をフリスクケース（センサー部）の上に載せてみました。すると、2μSv/hを少し超えるあたりの値を推移します。
ポケットガイガーを買ったは良いけれど、特に何かを計る必要性も感じていなかったこともあり、ポケットガイガーは「タンスの肥やし」になっていました。
しかし、それは何だか少しもったいないというわけで、この「土サンプル」がほのかに発する放射線とポケットガイガーを使って、何か試してみようかと考えています。
2012-04-06[n年前へ]
■iPhone 4にサブピクセル・レンダリングをすると978 dpiの高解像度になる!?
液晶ディスプレイを使うコンピュータ（ノート・デスクトップ）では、サブピクセルレンダリングを行うのが一般的です。サブピクセルレンダリングというのは、RGBの色素子を使って表示デバイスなら、色素子の配置も利用した上で、高解像度表示を行おうとする技術です。そういったサブピクセルレンダリング技術は各社使っていて、たとえばMicrosoft であれば ClearTypeと呼ばれています。
少し意外なことに、iPhoneやiPadではサブピクセルレンダリングは行われていません。たとえば、右の拡大写真を見ると、単純なアンチエイリアシング処理が行われているのみだということがわかります。
iPhone 4 の液晶の解像度は326 dpiですが、日本語の表示にはまだまだ不十分です。となると、iPhone 4でサブピクセル・レンダリングをさせることで、326×3=978dpi( いわゆる”相当” ）の超高解像度ディスプレイにしてみたくなります。
…というわけで、作ってみたのが、次の３種の画像です（ファイル置き場）。iPhone 4/4sのユーザが（縦位置で）この画像を眺めてみれば、iPhone 4での「デバイス解像度表示」「（iPhone4/4sが用いている）アンチエイリアシング表示」「（iPhone4の色素子配置を前提とした）サブピクセルレンダリング表示」の違いを眺めることができます。
- 960ピクセル×640ピクセルでレンダリングした画像
- 1920ピクセル×1280ピクセルでレンダリングした後に、960ピクセル×640ピクセルに解像度変換することでアンチエイリシングした画像
- 960ピクセル×（640×3）ピクセルでサブピクセルレンダリングした画像
iPhone 4でこれらの画像を眺めると、「デバイス解像度表示」では解像度が十分とは言えない、ということでした。解像度が低いと、「太さや感覚の不均一さ」が目についてしまいます。そんなことを感じざるを得ないデバイスで文字を読むと、少しストレスがたまりますから、つまり、326 dpi 程度では解像力は十分ではないな…と実感させられます。
そして、「（iPhone 4/4sが用いている）アンチエイリアシング（オーバーサンプリング）表示」も「サブピクセルレンダリング表示」も濃さのムラや色ムラが気になるけれど、「デバイス解像度表示」よりは「良さそう」と思わされます。…そして、調整の大変さ・安定性を考えると、iPhone 4/4sが用いているアンチエイリアシング（オーバーサンプリング）が、（現状では）一番良さそうに思えます。
2012-04-10[n年前へ]
■「Swatch 腕時計のベルト交換」と「オンデマンド・ベルト作成サービス」
Swatch腕時計「Dream Of Atom（鉄腕アトム）」（宝塚の手塚治虫記念館と京都駅ビルの２箇所でのみ販売）のベルトの表面コートがはがれ・浮いてきたので、3DなSwatch腕時計「3D Experience」のベルトと交換してみた。この「３D Swatch」は、発売時期から十年以上経った頃、”未使用品”としてバザーで500円ナリで購入したものだ。クオーツなのに時間がみるみる間に狂っていくという一点を除けば、何の問題も無かったのだが、その一点が腕時計としては致命的だったのだ。
（留め金の金属棒を抜き差しし）ベルトを入れ替えてみると、「Dream Of Atom（鉄腕アトム）」の文字盤は「透明・スケルトン」だったせいか、「3D Experience」のベルトとも似合う。そして、「3D Experience」も青色がモチーフのデザインだったので、「Dream Of Atom（鉄腕アトム）」のベルトとも合うようだ（時計は狂うから役に立たないけれど）。右の写真は、ベルト（と時計本体を）交換した後の写真だ。
Swatchのビニールベルトは耐久性が低いから、Swatch腕時計を長く使おうと思うと、Swatch純正のSwatch用交換ベルト
しかし、デザイン先行型のSwatchならば、本来附属していたベルトと同じデザインにしたくもなる。必要に応じて、ベルトを（任意のデザインで）カラー印刷してくれるオンデマンド・サービスが欲しい。買った時と同じデザインのベルトを買い直したり、時には気に入った絵（漫画や方程式や！）や写真を使ったベルトに入れ替えてみたり、ということをしてみたい。
2012-04-11[n年前へ]
■「老眼」の症状は１０代から進行し、ついには無限遠ですら”近くて見えなく”なる！
学生の可能性を可能にするポータルサイト ワンダーノーツに『「老眼」の症状は１０代から進行し、ついには無限遠ですら”近くて見えなく”なる！』を書きました。
大学に入りたての新入生が１０年経って博士課程を卒業しようとしている頃までには、４ｃｍくらい老眼が進んでいるのです。
すなわち、無限大ですら”近くて”（！）眼のピントが合わなくなってしまう！」という状態になってしまうのです。
2012-04-12[n年前へ]
■「遠視の人は老眼になりやすい？」の謎を解け！
「眼の（ピントの）調整範囲」は、年齢が同じであれば、たいてい同じくらいです。ただ、そこには「オフセット」があります。つまり、近い側にピントが合うという人と、遠い側にピントが合う、というオフセットです。前者は近視と呼ばれ、後者は遠視と呼ばれます。
近視や遠視の人は、メガネやコンタクトレンズをすることで、眼の（ピントの）調整範囲のオフセット（ズレ）を打ち消します。たとえば、ピントが合う領域が近い側にオフセットしている近視の人であれば、メガネをかけることで「裸眼時の眼のピント調整範囲（実線）」を「メガネをかけた状態のピント調整範囲（点線）」へと変え、（よく眺める距離領域や）無限遠が見えるようにするわけです。
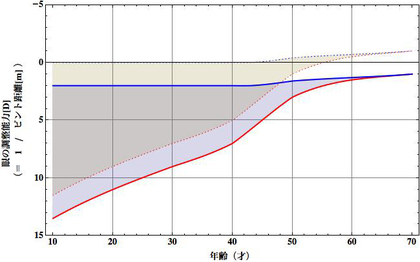
「眼の（ピントの）調整範囲」は、オフセットはありますが、年齢が同じであればたいてい同じくらいであって、「年をとるにしたがい、眼の（ピントを合わせることができる）調整範囲が狭くなる」ことが「老眼」です。だから、「老眼」は遠視の人にも近視の人にもモレなくやってきます。
しかし、「老眼」というものを「（裸眼で）近くが見えなくなること」だと感じる人も多いのではないかと思います。そういった感じ方を前提にすると、近視の人はメガネをとれば「ピントが合う領域が近い側にオフセットしている」わけですから、年をとって老眼になったとして、メガネをとって裸眼にしてしまえば、比較的近い側を見ることができる、ということになります。（もちろん、メガネをとってしまうということは、無限遠や遠くは見ることができなくなります。それは遠視の人が老眼鏡をかけることと同じです）
「遠視の人は老眼になりやすい？」と言われたり、それと反するように「遠視であっても近視であっても、老眼にはなるんだ」と言われたりします。そこで感じる矛盾は、「老眼」の定義（その言葉をどう考えるか・受け止めるか）が少し互いにズレていることが原因です。
そんな「ズレ」も、上に挙げたようなグラフを眺めれば、自然に溶かし・納得できるように思います。
2012-04-13[n年前へ]
■エクセル（表計算ソフト）の「表空間と値の拡張」を考える!?
エクセル（Microsoft Excel）に「型」を追加する機能が欲しいと思うことがあります。たとえば、複素数やベクトルをひとつのセルで扱ったり、さらにはもっと複雑な属性を持つ「値」を扱いたい、と思うことがあります。
そうした「（独自の）型」に対して、演算子を自由に定義できたり、セル内での表示方法を自由に定義できたり（「条件付き書式」の自由度が高ければ、独自型の表示スタイルをカスタマイズすることもできるのでしょうか）したい、と思うことがあります。
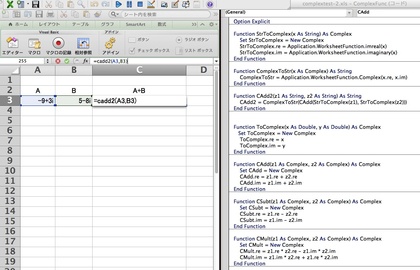…とそんなことを書いたら、ささっと @IchiroMori さんがシート（コード）を書いて・送ってくれました。「セルに入っている文字列を"imreal"と"imaginary"関数で処理し、独自定義の複素数クラスで処理した上で、"Complex"関数で文字列に戻すというコードです。
表計算ソフトというものを考えたとき（エクセルは表計算ソフトという範疇にとどまらないものだと思いますが）、表計算ソフトの基本機能は『「表」上で「値」が簡単に計算できる』ということになります。
そして、そんな表計算ソフトに対して、次の２つの点の拡張をしてみたいと感じることがあります。
１．「表」という部分
格子状の座標だけでなく、任意の「位置関係」「座標系」「空間」…を使いたい
２．「値」という部分
任意の属性・特性を持つ「存在（クラス・インスタンスというか）」を扱いたい（属性・値の演算方法やセル・グラフ上での表示方法も含む）
表計算ソフト（エクセル）の性質『「表」上で「値」が簡単に計算できる』というものを、『空間が各領域で値（属性）を持ち、それらが空間上で作用し合う・作用させ合うことができる』と捉えるならば、その「表」と「値」の拡張ができたなら、一体どんなことができるようになるだろう？と考えたくなります。…空間が各領域で値（属性）を持ち、それらが空間上で作用し合うというのは「世界」持つ基本的な性質ですから、つまりそれは、表計算ソフトが簡単に世界を表現しうるということになります。
「値」の拡張という部分に関しては、独自クラスを定義した上で文字列にシリアライズ・文字列からデシリアライズすれば可能だろうとは思うのですが、演算子や関数をオーバーロードできないと、既存関数の再利用ができなくなったり、何より「使い勝手」が悪くなるように思います（たとえば、ある属性に対して+=PLUSを定義したとき、その定義がSUM 関数やAVERAGE関数に反映されないと不便ですよね？）。
…というわけで、表計算ソフトの「表」と「値」の機能拡張ができたなら？と考えるのです。そうすれば、表計算ソフトは、（ある範囲の）世界を表現するのではないかと考えたりするのです。
2012-04-14[n年前へ]
■大人が「手に入れるべきもの」「忘れないでいたいもの」
江國香織が22人のインタビューイに「子供のころの話」を聞き、その時代を振り返る大人の言葉を文章にした「十五歳の残像
十五歳の頃、それから年を経た頃、時間が経っても同じ事も多ければ、少しの「違い」もあったりします。その「違い」は良いとも悪いとも…どちらとも言えない、「違い」です。良いとも悪いとも言えないものを時に身につけ、時に失ってきたとしたら、それら「両刃の剣」を両面から眺め、それらを忘れないでおこうと願い、十五歳の大人の言葉を眺め直してみました。
「どんどん矛盾していくよね」→矛盾を受け入れる。けれど、その矛盾を生み出す「限り・限界」を当たり前と受け入れない。
「でも、表現するということはそういうことでしょう？イメージをある程度限りある形で強く打ち出していく、というのが表現ななんだから」
甲斐よしひろさん
「無神経でいようと思ったら、いられるようになったことかな」→無神経さを手に入れる。それと同時に、感受性を失わない。
宮本文昭さん
「自分をごまかす、とか、許す、とか、そういうことは長けてきたと思います」→自分をごまかす・許すという「弱さ」というか「強さ」を身につけると同時に、そうしない「若さ」を忘れないようにする。
おすぎさん
聡明なひと、というのはつまり、絶望の認識のあるひと、ということなのだろう。ただし、長塚さんの言葉にはとても肯定的な響きがあって、…私はちょっとほっとした。→「絶望の認識」をもちつつ、「肯定」をあきらめない。
長塚京三さん
言葉のひとつひとつに、必ず論理的必然性というか、原因と結果が備（そな）わっている。双六（すごろく）風に正確に一歩づつ先にすすめていく話し方だ。それも、聞き手がとりのこされないように丁寧に、きちんきちんと手順を踏んで。
公文 公さん
2012-04-16[n年前へ]
■エクセルで２次方程式の「解の配置」を図示してみる!?
（たとえば）２次方程式、つまりx^2+bx+c==0という方程式の実数解を、中学生か高校生の頃、グラフにしてよく眺めたような気がします。しかし、それらの方程式がいつも１個か２個の解を持つにも関わらず、グラフにして眺めるのは「（時にはゼロ個の）実数解」だったような気がします。
そこで、今日は「複素数係数を持つ２次方程式の（複素数）解を”可視化する”エクセルシートを作ってみました（ダウンロード先）。"b"と"c"という２つの複素数を入力すると、（ある程度の範囲の）任意の複素数を"x"とした上で"x^2+bx+c"を計算し、その計算結果がゼロ近くになる部分（どんな複素数値を”ｘ”に代入すれば"x^2+bx+c"という式がゼロになるか）を複素平面上で”可視化”する、というエクセルシートです。
実数（あるいは時に複素数の）係数b,cを持つ２次方程式の、それら係数b,cを自由自在に動かしてみた時の２次方程式の２つの解（の配置や動き方）を眺めてみると、何だかとても面白いものです。たとえば、実数係数の２次方程式を作った時には、実数軸に線対称な２つの共役数が解になったり、複素数係数を入れてみると…何だか綺麗な対応が見えてきたり…と不思議に魅力的な世界が見えてくるのです。
明日は、「係数」をドラッグ＆ドロップで動かすと、「解」がどんな風に・どんな配置で動き回るかでも眺めてみよう（眺められるソフトでも作ってみよう）と思います。
2012-04-17[n年前へ]
■百次方程式の係数を複素平面上で動かして、百個の解のダンスを眺め・楽しんでみよう!?
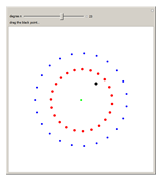多項式からなる代数方程式の「係数」をマウスでつかんで動かした時に、「（その代数方程式の）”解たち”の配置」と「”解たち”が動き回るようす」を眺めたいな…と思ったのですが、ググってみると「x^n + b x + 1 = 0 おいう代数方程式の係数bを複素平面上で動かした時に”解たち”がどのような配置になるか・どのように動き回るか」をインタラクティブに味わえる・楽しむことができる（Monodromy of z^n + b z + 1 = 0）というものがありました。
そこで、”x^n + b x + 1 = 0”という二次から百次までの代数方程式で、係数”ｂ”を複素平面上で（マウスで）動かして（青丸）、（その動きに応じて）解の集団（赤丸）が形作る美しいダンスを眺め・楽しんでみました。
中学生くらいの頃、"X^2+2=0"といった方程式を（各々の軸が実数の）XY平面上で黒板の上で眺めつつ、その黒板上に描かれたXY平面には、"Y＝X^2+2"というグラフと"Y=0"というグラフが「どこでも交わっていない」ようにしか見えないのに、方程式の「答え」は「（どこかに）２つの解がある」というもので…それは理不尽で不思議で…つまりは納得できなかったような気がします。
あの頃、複素平面上に複素数値を描いたグラフを見ていたら、黒板の上で多項式の解が複素平面上で円を描いてフォーク・ダンスを踊る風景を眺めていたら…数学に恋をしていたかもしれない、と思います。
オクラホマ・ミクサーやマイムマイム…黒板の上の複素平面上で代数方程式の係数が動くにつれ、その方程式の解の群団が踊るフォークダンス…が今日見た景色、です。
2012-04-19[n年前へ]
■Lytro リフォーカス・カメラの「写真」の色情報・深度情報を立体的に眺めてみる!?
撮影後にピント位置を自由自在に変えることができるというリフォーカス・カメラLYTROが発売されています。
このLytro の「写真」から色情報と深度情報を取り出し、立体的に眺めてみました。たとえば、そんな風にLytroが撮影した風景を立体的に眺めてみた例が、下の２つの動画です。
これらの立体空間を作る手順は、
- LytroのWEB 表示用Flashが表示時にサイトからダウンロードする"output.noframes.lfp"（深度マップが入った画像ファイル）をローカルに保存
- Lytroカメラの画像から（nrpatel/lfptoolsを使い）深度マップ・深度毎の色画像群を抽出
- 深度マップをもとに色画像群からパンフォーカス画像を生成
- 深度マップにパンフォーカス画像をテクスチャマッピングして立体表示
ちなみに、上の動画に使った元画像はこちらで、下の元画像はこちらです。この手順では、WEB表示の「ギャラリー」に飾られている「写真」を使っているので、「Lytroカメラを持っていなくても・やってみることができる」というのがミソです。
ちなみに、抽出した深度マップは、適当にこんなRubyコードを書いて、一端CSVファイルにしてから処理してみました。
filePath = ARGV[0]
width = ARGV[1].to_i
x = 0
data = []
open(filePath) do |file|
file.readlines.each do |line|
data << line.to_f
x += 1
if x == width
puts data.join ','
x = 0
data = []
end
end
end
2012-04-20[n年前へ]
■Lytro "リフォーカス" ”ライトフィールド”カメラを使ってみた。（第一回）
撮影後にピント位置を自由自在に変えることができる”リフォーカス・カメラ”、”ライト・フィールド・カメラ”とも呼ばれるLYTROカメラを使ってみました。街中や部屋の中…たくさんの場所で撮影した「写真」の一部が、たとえば、こんな写真です。顕微鏡や赤提灯、ビー玉やホログラム…たくさんのものを、とても楽しく・ワクワクしつつ、LYTROのファインダー越しに眺めました。
こうした機能（あるいは、その機能を使い得られた情報の活用）は、少なくとも数年後には「当たり前で・普通のこと」になっているはずだと思います。
「ムーアの法則」のごとく、デバイスの規模・機能は常に等比的に増大・進歩するし、それ以上に、デバイスから得た情報を処理するソフトウェアも発展しているはずだと信じます。…デバイスは、一日一歩、三日で三歩、３６５日で３６５歩進んでいるはずだと思いますし、それらの光学系デバイスから（直接）得ることができる以上の「感動」を与える機能が、ソフトウェア機能を介して、「未来のカメラ（レンズ）」には搭載されているだろうと思います。
つまり、私たちが感じる感動を１２０パーセント（つまり、人が感じる以上の感動を）そっと差し出す機能が、未来のLYTROには搭載されているはずだと思うのです。
2012-04-22[n年前へ]
■（競技場の）明るさをJIS規格で比べてみると、明るさ選手権は「格闘技の舞台」がナンバー１！
学生の可能性を可能にするポータルサイト ワンダーノーツに『（競技場の）明るさをJIS規格で比べてみると、明るさ選手権は「格闘技の舞台」がナンバー１！』を書きました。
ためしに、「この明るさ（照度）にしなさい」という決まりを、競技場の（一番明るい場所を）明るい順番にトップ５を並べてみると、つまり「明るさ選手権」を開催してみると、こんな具合になります。 ちなみに、プロ野球など向けには、内野や外野…など場所によって「明るさの決まり」は違っています。 （たとえば、プロ野球の外野は”内野よりかなり暗い”1200ルクスと決められています）
2012-04-23[n年前へ]
■ぼくらが見慣れた２次方程式のグラフは…「胸の谷間」の方程式だった！
中学生か高校生の頃、XY平面の上にy=x^2+1といった２次方程式のグラフを描き、さらにそのXY平面の上にy=0という直線を描き、そのふたつのが交点を持たないので、x^2+1=0という方程式は実数解を持たない…という説明を聞いた覚えがあります。
けれど、２次方程式の解の公式を解けば、そのy=x^2+1という方程式は２つの解、２つの複素数の解を何処かに持っている…という説明を聞きながら、何だか腑に落ちなかったような気がします。
先日、「複素数係数を持つ２次方程式の（複素数）解を”可視化する”エクセルシート」を作ってみましたエクセルで２次方程式の「解の配置」を図示してみる!?）。そして、x^2+1=0という方程式の解を眺めながら、ふとこんなことを思いました。
なんだ、これがぼくたちの探している青い鳥なんだ。
ぼくたちは、ずいぶん遠くまで青い鳥を探しに行ったけど…
本当は、いつもここにいたんだ。
複素空間上に、実に単純な２次方程式が描く曲面は、ふたつの（まるで胸のような）ふくらみを見せ、…x^2+1=0という方程式こそが、人を魅惑する何よりホンモノの「おっぱい曲面方程式」だったのではないか、と思ったのです。これまでに、たくさんの「おっぱい方程式」を眺めてきたけれど…x^2+1という思春期に眺めた式こそが、本当のおっぱい方程式ではなかったか…と気づいたのです。
たとえば、下のグラフは複素空間上でx^2+1という式で求められる値と０という値の間の距離（ユークリッド・ノルム）を（縦軸を反転しつつ）描いてみたものです。つまり、それはx^2+1=0という方程式への「複素空間上での解への”近さ”」をグラフにしたものです。
i(アイ)と-i(アイ)という虚軸上に頂（いただき）、すなわち解を位置させる「ふくらみ」は、それはまさに「おっぱい曲面」を感じさせます。…というより、これが「おっぱい」でなかったら、一体何だというのだ…という姿形をしています。けれど、この「美しい曲面」は、ただ複素空間上に描かれた ”x^2+1”というだけの曲面です。
そして、こんなグラフを眺めながら、…ぼくらが見慣れた実数で描かれたXY平面上の２次方程式のグラフは…複素空間上にあるはずの「おっぱい曲面」上に（ふたつの胸を分けるように）描かれた一本の曲線だった！…私たちが見慣れたあの曲線は「（魅惑の）胸の谷間の方程式」だった！と気づいたのです。
たとえば、上のおっぱい曲面を２分するように描かれた黒い線こしが、黒板の上に繰り返し眺めたはずの”y=x^2+1”という、単純で見慣れた２次曲線です。
中学生の頃、黒板の上に見た「XY平面上に２次方程式のグラフ」は「胸の谷間の曲線」であったし、その魅惑曲線の向こうには複素空間上のおっぱい曲面があった…なんて、何だか凄いと思いませんか？
ふたつの胸のふくらみは、
何でもできる証拠なの。
「魔女っ子メグちゃん」
2012-04-24[n年前へ]
■「"稼ぐ力"」と「（機械が働き）人が働かずに暮らせる未来」
フリーペーパーR２５に、日本は莫大な所得収支があるから、日本の”稼ぐ力”に関して悲観する必要は無い、という論調の経済解説記事が載っていた。
…「日本の”稼ぐ力”が弱くなった」と悲観的な論調が目についた。貿易がダメだと日本は稼げない、と言わんばかりだった。
（中略）２００５年から、貿易以上に日本が稼いできたものがあったのだ。それが「所得収支」である。海外に投資をすることによって得た、利子や配当などのリターンである。
（中略）本当に「日本はもう稼げない」などと悲観しなければいけないことだったのか。
こどもの頃、SF小説を読みながら、機械がいる未来を夢見た。
…農場では機械が農作物を作ってる。農場で作られた麦からは、工場で機械が自動作業でビールを作り、人はビールを飲みながら、本を読んでいる。つまりは、機械が人間の代わりに働き、そして、人間は”働かずとも優雅に過ごす”ことができる世界である。
今、日本の工場では、たくさんの機械たちが働いている。ただ、こどもの頃の想像と大きく違ったのは、自動機械（ロボット）が働いても「自動機械の持ち主（それは”お金持ち”だ）」にお金が入ってくるだけだ、ということだった。そして、自動機械の持ち主でなく、働いていない種類の人類には「タダでどこからかビールが運ばれてくる」わけではなかった、ということだった。
「所得収支があるから、日本の”稼ぐ力”に関して悲観する必要は無い」という解説を読んで、こどもの頃に想像した「（機械が働き）人は働かずとも優雅に暮らせる未来」を思い出した。
７０年代、こどもが想像した未来像は間違っていた。「（機械が働き）人は働かずとも優雅に暮らせる未来」は、「機械を持つもの」にだけ当てはまる世界だった。そして、もちろん、働かなくて良い世界を夢見た（怠惰な）こどもは、機械を持つ側ではなかった。
2012-04-25[n年前へ]
■割れたiPhoneディスプレイに「セルラ・オートマトンの芸術」を見る!?
街中で、iPhone4を落とした。左手をスルリと抜けだし、クルリクルリと回転しつつ、iPhone4は空中にダイブした。無重力状態を十分堪能した後、iPhoneはコンクリートの上に見事に画面を這いつくばらせるように着地して、ガラスが割れた。
その割れ目を眺めてみると、これが雪崩や砂の割れ目実験結果のようで、何というか実に美しい。直線的に伸びる亀裂の途中から、新たな亀裂が伸びていく。その亀裂は、綺麗に二等辺三角形を描き、全体として絶妙なピラミッド模様を形作っている。…セルラ・オートマトンが描き出す「進展模様」をも連想させ、科学美術館のようで、これは実に美しい。
iPhoneが、コンクリートの上にぶつかった瞬間、一体、どんな応力が生じ、どんな破壊の進展があったのだろうか？
2012-04-26[n年前へ]
■”コンパクトデジカメ”だけで「本をめくるだけの最速”自炊”」をするワザがある！
本の頁をパラパラめくり、それをiPhone撮影・処理することで、書籍を”非破壊””最速”に電子化をする『最速自炊カメラ「Jucie」』はとても便利です。
しかし、iPhone を持っていなくとも、（いくつかの）コンパクト・デジカメのユーザであれば、実は同じようなことができるのです。つまり、デジカメのレンズの前で「本のページをめくるだけ」で、紙の書籍を電子化することができるのです。
CHDKというコンパクト・デジカメのファームウェアをハックするツールがあります。このツールを使うと、「CHDKユーザたちが作ったさまざまな拡張機能」を使うことができて、その拡張機能の中には「動くものを検知する機能」もあるのです。そして、その動体検知機能を使い、「本のページをめくるだけで、紙の書籍を電子化することができるようになる拡張機能(Document Archival Motion Detection Script for CHDK)」も作成されているのです。つまり、”コンパクトデジカメ”だけで「本をめくるだけの最速”自炊”」をする機能も提供されている、というわけです。
この拡張機能(Document Archival Motion Detection Script for CHDK)」は、ページをめくり・位置を揃える動作を監視し、その作業が終わった後に「ページ撮影」を行います。そして、またページめくり動作が行われるのを監視・待機する…という動作を行います。三脚にカメラを固定して、カメラの前で本のページをめくっていけば、自動的に、なおかつ、高画質にすべてのページがカシャリ・カシャリとカメラの中に撮影され、紙の書籍が電子化されていきます。
iPhone を持っていないけれど、「本をめくるだけの最速”自炊”」をしてみたいという人は、（もしもCHDKを使うことができるコンパクト・デジカメを持っているなら）”Document Archival Motion Detection Script for CHDK”を試しに使ってみると、面白いかもしれません。
2012-04-30[n年前へ]
■ゴルゴ１３は「ライフル弾の品質管理」に実は意外と甘かった!?
学生の可能性を可能にするポータルサイト ワンダーノーツに『ゴルゴ１３は「ライフル弾の品質管理」に実は意外と甘かった!?』を書きました。
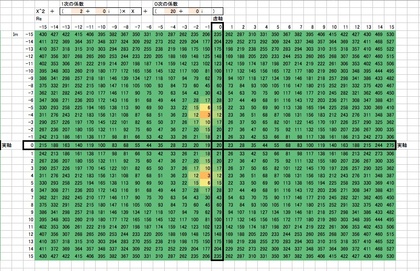
3パーセント強の不良品が混じっている恐れがあるということは、ゴルゴ１３が３０回くらい依頼を引き受けたなら、一回くらいは「ライフル弾が不発して（あるいは暴発して）依頼遂行に失敗する」という事態に陥りそうです。 ゴルゴ１３の仕事術は、何事も「一発必中」「一発で片をつける」をモットーにしているので、その一発が不発弾だとにっちもさっちもいかなくなってしまいます。
あなたがゴルゴ１３なら、自分のライフルに詰めた銃弾の不良率が3.4パーセント（かもしれない）と聞いたら、どう考えるでしょう？「品質管理」をもっと厳しくする、あるいは、一発必中の仕事術を止める…？危機管理と言えば天下一品のはずのゴルゴ１３は、そこのところどう考えているんでしょうか？
」など。