2012-09-01[n年前へ]
■「38℃の風呂に完全全身入浴時の、人体周り熱収支」を考えよう!? 
 中学生が行った自然観察コンクール作品「38℃の日は暑いのに38℃の風呂に入ると熱くないのはなぜか」が面白かった。風呂の中でシュノーケリング全身潜水実験をしたり、服を着たまま風呂に入ったり…という辺りは、探偵ナイトスクープばりのバカバカしさで最高に楽しめる。「それはどうだろう?」と思うデータ解釈や論理もあるけれど、とにかく魅力的だ。
中学生が行った自然観察コンクール作品「38℃の日は暑いのに38℃の風呂に入ると熱くないのはなぜか」が面白かった。風呂の中でシュノーケリング全身潜水実験をしたり、服を着たまま風呂に入ったり…という辺りは、探偵ナイトスクープばりのバカバカしさで最高に楽しめる。「それはどうだろう?」と思うデータ解釈や論理もあるけれど、とにかく魅力的だ。
ところで、「38℃風呂の中でシュノーケリング全身潜水実験」を、ある程度長い時間、たとえば10分程度したとしたら、体温そして皮膚温は一体どうなるだろうか? 人間は、70ワット程度の発熱体である。 ということは、毎秒70ジュールの熱を体から排出しなければ、人の体温は刻々上昇してしまう。 もし、人体の比熱が大雑把に水とほぼ同じだとしてしまうなら、たとえば体重50kgの人がいたとすると、1分あたり0.2℃ほど体温の上昇が続く計算になる。
 風呂の中に全身が浸っていると汗をかいても体を冷やすことはできないから*、結局のところ、体温は38℃より少し高いところに落ち着いて、その38+アルファ℃の体から、38℃の風呂のお湯に向かって熱が流れていくことになるのだろう。そして、皮膚温は38+アルファ℃よりは低く、けれど38℃の風呂温よりは高い程度で落ち着くことになる。
風呂の中に全身が浸っていると汗をかいても体を冷やすことはできないから*、結局のところ、体温は38℃より少し高いところに落ち着いて、その38+アルファ℃の体から、38℃の風呂のお湯に向かって熱が流れていくことになるのだろう。そして、皮膚温は38+アルファ℃よりは低く、けれど38℃の風呂温よりは高い程度で落ち着くことになる。
水の熱伝導度を考えると、1℃弱くらい水温より体温が高い程度で平衡状態になるという具合だろうか。そうだとすれば、もしも「38℃風呂の中でシュノーケリング全身潜水実験」を少し長い時間・キッチリやったなら、38℃の風呂は間違いなく(体より)冷たいと感じることになりそうだ。
38℃の風呂に完全全身入浴時に、一体「人体周り熱収支」はどんな風になるだろう。?計算はしてみることにしても、中学生の彼ら(彼女ら)を見習って、銭湯にでも行ってシュノーケリングしてみることにしようか…。
2012-09-02[n年前へ]
■「入道雲が空高く届くためのエネルギー」はどこから来るか!? 
夏の終わり、青い空に白い入道雲が立ち上り、色のコントラストがとても綺麗です。地表近くで暖められた空気が上昇気流を作り、ある程度の高度で雲を作り出して…といっても、どうして、あんなに空高くまで上昇していくことができるなんて不思議だ、とも思えます。

上空で入道雲が生まれると、その入道雲が生まれたことでさらに上昇気流を生み、その上昇気流がさらに雲を作り、その雲がさらに上昇気流を…という具合に、入道雲は「大きく育ち・成長する」運命を持っています。
 上昇気流ができ・空気が上に上がっていくと、高度が上がるに連れ気圧が低くなるため、その空気は膨張するとともに温度が下がっていきます(100m上昇するごとに約1℃)。そして、空気の温度が下がり・空気の中に含まれていた水蒸気が水滴に変わる高度まで(もしも)辿り着くことができたなら、空気中の水蒸気が水滴に変わるにともなって熱が放出され、その水滴=雲を生み出した(水蒸気を含んでいた)空気を暖めます。
上昇気流ができ・空気が上に上がっていくと、高度が上がるに連れ気圧が低くなるため、その空気は膨張するとともに温度が下がっていきます(100m上昇するごとに約1℃)。そして、空気の温度が下がり・空気の中に含まれていた水蒸気が水滴に変わる高度まで(もしも)辿り着くことができたなら、空気中の水蒸気が水滴に変わるにともなって熱が放出され、その水滴=雲を生み出した(水蒸気を含んでいた)空気を暖めます。
そんな、空気が雲が生み出しつつ上昇しているような状態では、高度が100m上がるごとの温度低下は0.5℃程度になりますが、その一方で周りの空気は高度100mごとに約0.65℃温度が低下していくので、相対的に、周囲の空気の高度に対して温度がどんどん高くなり、さらに上昇気流を生む、というわけです。
蒸し暑い中、空高く伸びる入道雲を眺めつつ、「地表近く、自分の周りを取りまく暑い湿気た空気が上昇していったとき、どの程度の高度まで届くことができるだろう?」と感じたので、それを非常に大雑把な計算で見積もってみることにしました。
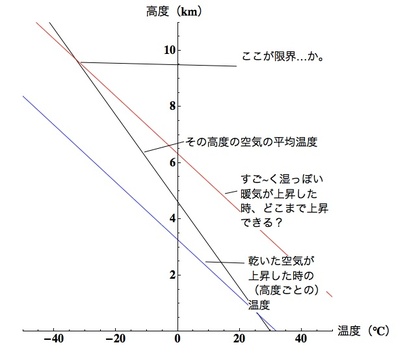 まず、地表の温度が30℃で湿度50%だとして、周りより2℃ほど暖かい空気の塊が生まれ上昇していくことを考えます。計算を簡単にするために、空気塊に含まれている水蒸気が雲に変わるときに発生させる熱エネルギーを(いきなり地表で)空気に対して与えてしまうことにします。…すると、空気塊は30+2+30=62℃相当になります。そして、高度100m上昇するごとに1℃づつ断熱膨張で温度を低下させ、周囲の空気(100mごとに約0.5℃づつ温度が低下する)と温度が一致する高度を求めてみましょう(右図)。
まず、地表の温度が30℃で湿度50%だとして、周りより2℃ほど暖かい空気の塊が生まれ上昇していくことを考えます。計算を簡単にするために、空気塊に含まれている水蒸気が雲に変わるときに発生させる熱エネルギーを(いきなり地表で)空気に対して与えてしまうことにします。…すると、空気塊は30+2+30=62℃相当になります。そして、高度100m上昇するごとに1℃づつ断熱膨張で温度を低下させ、周囲の空気(100mごとに約0.5℃づつ温度が低下する)と温度が一致する高度を求めてみましょう(右図)。
すると、地表から高度にして9kmほどの上空で「入道雲」の温度と周りの空気の温度が一致することになります。つまり、気温30℃・湿度50%程度で、周りより2℃暖かいくらいの上昇気流は、(とても大雑把な見積もり方をすると)入道雲になって10km程度の高さまでモクモクと立ち上っていくことができそうだ、というわけです。
 上昇気流が入道雲を生み、その入道雲が生まれることで上昇気流をさらに作り出す、雲を生み出す水分がある限りモクモクと上昇し続ける…入道雲のポジティブ・フィードバック・ループ・システムは安定からはかけ離れた限りなく不安定なシステムです。けれど、それも何だか「夏」らしくて気持ち良く思えます
上昇気流が入道雲を生み、その入道雲が生まれることで上昇気流をさらに作り出す、雲を生み出す水分がある限りモクモクと上昇し続ける…入道雲のポジティブ・フィードバック・ループ・システムは安定からはかけ離れた限りなく不安定なシステムです。けれど、それも何だか「夏」らしくて気持ち良く思えます
2012-09-03[n年前へ]
■パノラマ画像で眺める「巨人阿倍の空中バウンド・ホームラン」の秘密!? 
 「突然、空中でバウンドするような軌道で、バックスクリーンに飛び込んだ」という巨人 阿部選手の横浜DeNA戦ホームランの話(「阿部の打球は本当に曲がったのか?」)が面白かったので、TV動画から「カメラマンが操作したズームなど”カメラワーク”の影響を除去した上で・ホームランボールの軌跡を映し出す」スクリプトを書いて、阿倍の打球が「空中バウンド」した辺りの映像を「パノラマ画像」にしてみました。
「突然、空中でバウンドするような軌道で、バックスクリーンに飛び込んだ」という巨人 阿部選手の横浜DeNA戦ホームランの話(「阿部の打球は本当に曲がったのか?」)が面白かったので、TV動画から「カメラマンが操作したズームなど”カメラワーク”の影響を除去した上で・ホームランボールの軌跡を映し出す」スクリプトを書いて、阿倍の打球が「空中バウンド」した辺りの映像を「パノラマ画像」にしてみました。
そうして眺めてみると、特に奇妙でもない普通の打球(軌跡)に見えます。…なるほど、確かにナイトゲームとカメラワークが、奇妙で不思議な空中で突然方向を変えるホームラン、ミステリアスな魔法のホームラン・ボールを生み出したのかもしれないと感じますね。

問題の打球は8月26日の横浜DeNA戦(横浜)の6回、阿部が左腕・篠原貴行投手(35)から放った19号2ラン。高い弧を描いて下降をはじめ、中飛かと思われた次の瞬間、突然空中でバウンドするような軌道でバックスクリーンに飛び込んだのだ。
曲がっているように見える原因は、ズームだったわけです。夜の球場で視覚的情報量が少ないことからズームに気づきにくく、そのためボールが曲がったように見えたというのが私の結論です。
この解析のために書いたMathematicaコード・アルゴリズムは、『パノラマ画像で眺める「巨人阿倍の空中バウンド・ホームラン」の秘密!?』で読むことができます。
2012-09-04[n年前へ]
■続 パノラマ画像で眺める「巨人阿倍の空中バウンド・ホームラン」の秘密!? 
 『パノラマ画像で眺める「巨人阿倍の空中バウンド・ホームラン」の秘密!?』で書いた”カメラワーク”の影響を除去した上で・ホームランボールの軌跡を映し出す」スクリプトを書き直してみました。たとえば、下に貼り付けた画像は、巨人阿部選手のホームランボールが外野上空を飛翔していく0.5秒ほどの動きを、一枚の画像として合成したものです。…そうして眺めてみると、見事なくらいの「綺麗で美しく自然極まりない放物線」を巨人阿部が打ったホームラン・ボールは描いていることがわかります。
『パノラマ画像で眺める「巨人阿倍の空中バウンド・ホームラン」の秘密!?』で書いた”カメラワーク”の影響を除去した上で・ホームランボールの軌跡を映し出す」スクリプトを書き直してみました。たとえば、下に貼り付けた画像は、巨人阿部選手のホームランボールが外野上空を飛翔していく0.5秒ほどの動きを、一枚の画像として合成したものです。…そうして眺めてみると、見事なくらいの「綺麗で美しく自然極まりない放物線」を巨人阿部が打ったホームラン・ボールは描いていることがわかります。
「突然、空中でバウンドする軌道のホームラン」…超常現象に思えるホームランボールの軌跡も、それは必然で単純な「カメラマンの指が(アングル的に必然として)操作したカメラ行列の変化によって作りされる「人の視覚の錯覚」だった、ということがわかります。

参考までに、昨日・今日に書いてみたMathematicaスクリプトをここに貼り付けておきます。処理手順を大雑把に書くと、「動画中のフレーム内から特徴点を抽出し、隣接フレーム間での特徴点位置関係からフレーム間の(カメラ)変換を算出して、その逆変換を使うことで一連の撮影映像を一枚のパノラマ画像に合成する、という具合です。(コードの前半は、オーバーレイ表示された文字や画像を除去するためのコードですから、本質的なものではありません)
frames=Import["hoge.mov", "ImageList"];(*画像読み込み*)
frames2=ParallelTable[
Sharpen[
ColorConvert[
ImageTrim[ frames[[i]], {{1, 190}, {1024, 720}}]
, "Grayscale"]
, 7],
{i, 1, Length[frames]}
];(*画像切り取り&強調*)
i1=frames2[[130]];i1search=frames2[[130]];
Do[
tr=FindGeometricTransform[
(*位置検出用画像と保存用画像は別にする*)
i1search,i2 = frames2[[i]] ,
"Transformation" -> "Affine"];
{w, h} = ImageDimensions[i1search];
tmp = ImagePerspectiveTransformation[
i2, tr[[2]],
DataRange -> Full,
PlotRange -> {{0, First@tr[[2]][{w, 0}]}, {0, h}}
];
{w, h} = ImageDimensions[tmp];
i1search = ImageCompose[i1, {tmp, 1.},
Round@({w, h}/2)];
i1 = ImageCompose[i1, {tmp, 0.75},
Round@({w, h}/2), {1, 0, -1}];
{i, 131, 140, 1}
];
il (* パノラマ画像 *)
ちなみに、隣接フレーム間から画像変換の関係式を導こうとすると、隣接フレーム間で対応する点を(回転や倍率を算出するために)最低3点抽出しないといけません。…というわけで、上記コードはホームランボール(という名前のただ一点の特徴点)だけが画面に映し出されているような映像があるとエラーを吐いてしまいます。
2012-09-05[n年前へ]
■トレンクルのチェーンリング交換 
 折りたたみ自転車トレンクルのフロント・チェーンリングを42Tから53Tに交換した。これで、ゆっくり走るにもクルクルクルクル…とペダルを回さなければいけない「カゴの中のハムスター状態」から脱出できそうだ。
折りたたみ自転車トレンクルのフロント・チェーンリングを42Tから53Tに交換した。これで、ゆっくり走るにもクルクルクルクル…とペダルを回さなければいけない「カゴの中のハムスター状態」から脱出できそうだ。
川沿いを走ってみると、街と街の間を行き来するくらいなら、気持ち良く走ることができる感じだ。チェーンリングとフレームの間には、まだもうすこしの隙間があるから、56Tのリングを探して・手に入れたら、また交換しようかな。
2012-09-06[n年前へ]
■「突き抜けた」選挙(候補者)ポスター展覧会 
個性溢れる(端的に言えば、かなり変わった「選挙(候補者)ポスターを」集め・並べてみました。街中を歩いている時、選挙ポスターが貼られていることに気づき、色んな候補者ポスターを眺めてみたくなったのです。
2012-09-07[n年前へ]
■「田舎と都会の電力事情と飲食店・風俗店の境界」や「apple][のビデオ回路」など 
9月7日の「n年前へ」から。

「飲食店・風俗店の境界と田舎・都会の境界」に関する議論がエンエンに続く参議院地方行政委員会。高田なほ子君と政府委員(原文兵衞君)のエンエンと続く会話はまさに喜劇。
「飲食店と風俗店、境界と田舎と都会」の境界線をルクスで計る(2004年)
apple][の回路は、14.32MHzのオシレータ出力を2分周した7.12MHzの信号がビデオ信号のドット・クロックとなる。(基本的には)1ドットが1bitの単純な構成だ。NTSCのビデオ信号のカラー情報は「ビデオ信号に重畳した3.58MHz波形」の位相で表すが、この3.58MHzはappleのビデオ・クロック(7.12MHz)のちょうど2倍である。ということは、2ドット分のビデオ・信号を"on""off"として出力した場合と、"off""on"して出力した場合では、NTSC信号でのカラー情報(位相)が180度ずれたもの(=補色)を表すことができる。
さらに、(ある時期以降の)appleの場合ビデオ・データの特定の(=横7ドット, 縦8ドットのテキストモードとの兼ね合いで使われていなかった最上位の)bitを立てると、フリップフロップ回路で70nsだけ信号を送らすことができる。その70nsのずれは、NTSCのカラー信号3.58MHzのドット・クロック幅の25%に相当する(角度で言うと90度)。ということは、NTSC信号でのカラー情報(位相)が0, 180度の色だけでなく、90, 270度の色も出力(疑似生成)することができるようになる。すなわち、黒・白・紫・緑に加えて青・橙という計6色が出力することができるようになる。
appleのビデオ機能(2005年)
飛び乗った東急東横線 各駅列車車両を隅から隅まで眺め、一体スピーカーがどこにあるのかを確認してみました。確認した結果の図、車両のどこに車内放送用スピーカーがあるかを描いてみたのが下の図です。この図を描いてみて、「私は列車の中で隅っこの席に好んで座っていたけれど、そんな”隅っこの席”14/16=87.5パーセントの確率で間近にスピーカーがあったのだ!」ということに気づきました。隅っこの席には、(今日、確認した東急東横線の車両では)非常に高い確率で「真上・正面・すぐ横」のいずれかにスピーカーがあったのです。
「うるさい電車の車内放送」を避けるためのテクニック(2011年)
2012-09-08[n年前へ]
■夢を売るグラビアアイドルには「(夢の)イリュージョンブラ」が似合うはず!? 
 以前、「カフェウォール錯視」を利用して、どんな小胸さんも、いえ小胸どころか凹凸が全くない完全に平面の胸ですら「マルマル飛び出す巨乳に見せてしまうイリュージョン・ブラ」を作ったことがあります。
以前、「カフェウォール錯視」を利用して、どんな小胸さんも、いえ小胸どころか凹凸が全くない完全に平面の胸ですら「マルマル飛び出す巨乳に見せてしまうイリュージョン・ブラ」を作ったことがあります。
…けれど、そのブラジャーの評判は「水着に使うならともかく、ブラジャーではほとんど役に立たない」という惨憺たるものでした。「ブラジャーは男性相手に見せるものではないし…見せるシチュエーションでも、その後すぐに脱いでしまう」というのです。
 そこで考えました。このイリュージョンブラは、グラビアアイドルには、素晴らしく重宝されるのではないでしょうか。「水着」と言えば、それはまさにグラビアアイドルにとっての制服のようなものですし、グラビアアイドルはそのブラならぬ水着を脱ぐことは決してありません(グラビアアイドルを”卒業”したら別かもしれませんが)。そんなグラビアアイドルたちの中には、「胸をもっともっと大きく見せたい」と切望している人さんだっているに違いありませんから、そんな小胸グラビアアイドルさんたちは、このイリュージョンブラを絶対に欲しがるに違いありません。
そこで考えました。このイリュージョンブラは、グラビアアイドルには、素晴らしく重宝されるのではないでしょうか。「水着」と言えば、それはまさにグラビアアイドルにとっての制服のようなものですし、グラビアアイドルはそのブラならぬ水着を脱ぐことは決してありません(グラビアアイドルを”卒業”したら別かもしれませんが)。そんなグラビアアイドルたちの中には、「胸をもっともっと大きく見せたい」と切望している人さんだっているに違いありませんから、そんな小胸グラビアアイドルさんたちは、このイリュージョンブラを絶対に欲しがるに違いありません。
というわけで、”Aカップ グラビアアイドル”で検索し、その筆頭で出てきたグラビアアイドルSさん(24才)の画像に、イリュージョンブラを(勝手に)着せてみました。
Cカップくらいあれば寄せたり上げたりする元の膨らみがあるからなんとかなるけど、私には元の膨らみが無いからなあ・・・(´・ω・`)変身前後の画像をクリックして拡大した上で(解像度の関係上、サムネイル画面ではイリュージョン効果を体感することができないのです)、「どのくらいグラビア巨乳度が高まっているか」を体感してみると、きっと面白いはずです。
無から有を生み出す魔法なんて私使えない(´・ω・`)
グラビアアイドルSさん(24才)


夢を売るグラビアアイドルには、夢のイリュージョンブラこそが似合うに違いない…と思いませんか?「無から有を生み出す魔法のイリュージョンブラならぬイリュージョン水着」は、(小胸の)グラビアアイドル必携の一品になるはすです。
2012-09-09[n年前へ]
■おっぱい解析向けライブラリを書いてみる!? 第1回 
 「おっぱい解析向けライブラリ」が無いのっておかしくない?とふと気づきました。たとえば、プログラミングする時、数学関数を使いたければmathライブラリーをインクルードすればOKという言語も多いと思います。しかし、「おっぱい解析」をしようとした時、ゼロからコードを書かなくてはならないというのは、非常に不便極まりない話です。「車輪の再発明をするな」というアドバイスを、なぜか、おっぱい解析の世界ではないがしろにされているようにも思われます。…そこで、地球上のおっぱい解析研究者のために、おっぱい解析向けライブラリを書いてみることにしました。
「おっぱい解析向けライブラリ」が無いのっておかしくない?とふと気づきました。たとえば、プログラミングする時、数学関数を使いたければmathライブラリーをインクルードすればOKという言語も多いと思います。しかし、「おっぱい解析」をしようとした時、ゼロからコードを書かなくてはならないというのは、非常に不便極まりない話です。「車輪の再発明をするな」というアドバイスを、なぜか、おっぱい解析の世界ではないがしろにされているようにも思われます。…そこで、地球上のおっぱい解析研究者のために、おっぱい解析向けライブラリを書いてみることにしました。
今日は、Mathematicaで「こんな感じ?」というラフスケッチを描いてみることにします。まずは、「アンダーバストとトップバストの差(cm)からカップサイズを求める関数cpu2cmと、カップサイズからアンダーバストとトップバストの差(cm)を求める関数cm2cupです。
cup2cm["AAA"] = 5; cup2cm["AA"] = 7.5;
cup2cm[cup_] := ((ToCharacterCode[cup] - ToCharacterCode["A"])*2.5 + 10)[[1]];
cm2cup[cm_] := If[cm <= 6.25, "AAA", If[cm <= 8.75, "AA", FromCharacterCode[Round[(cm - 10.)/2.5 + 65]]]];
このライブラリを使えば、
cup2cm["C"]
=15
cm2cup[30]というように、アルファベット表記のカップサイズとアンダーバストとトップバストの差(cm)の間を自由に行き来することができます。
=I
 しかし、実は「カップサイズ」も「アンダーバストとトップバストの差(cm)」もとても扱いづらく・ワナに満ちた表記なのです。なぜなら、ひとたび「おっぱい解析(特にカップサイズ)」を真面目にしようとしたならば、さまざまな矛盾に気づき・愕然とさせられます。(たとえば…という話は次回以降にしましょう)
しかし、実は「カップサイズ」も「アンダーバストとトップバストの差(cm)」もとても扱いづらく・ワナに満ちた表記なのです。なぜなら、ひとたび「おっぱい解析(特にカップサイズ)」を真面目にしようとしたならば、さまざまな矛盾に気づき・愕然とさせられます。(たとえば…という話は次回以降にしましょう)
というわけで、そんなオッパイに隠された深遠なるミステリーを解き明かすために、引き続き「おっぱい解析向けライブラリ」を書きながら、おっぱい解析の基本・応用例題を解き・楽しんでみることにしましょう。
C# でおっぱい解析向けライブラリを書いてみる!!
世界で一番大きな天然バストのサイズは 102cm(ZZZ カップ) ということがわかりました。ZZZ は、cmとカップの変換公式からすると 77.5cmでしかないのですが、この記事を読む限りは、この値以上であればZZZカップ、という理解で良さそうです。
2012-09-10[n年前へ]
■「神秘の中国海軍潜水艦」や「量子通信衛星」「日本女性のイメージ」 
今週の「網博週報」ネタ も面白い。「神秘の中国海軍潜水艦」や「中国、2015年をめどに量子通信衛星の打ち上げを目指す」「外国人から見た日本女性のイメージ」など、楽しめる記事がてんこもり*。
*てんこ盛り(天こ盛り、てんこもり)とは、食器などに食べ物を堆く(うずたかく、盛り上がって高く)盛ること。また、その様子、その盛ったもの。山盛り、てこもりと同義。転じて(よくプラスイメージの)ものが豊富にある様子を「〜がてんこ盛り」と言ったりする。食べ物を普通より多く盛ることは大盛りという


スラッシュドットの「過去最長143kmでの量子テレポーテーション実験に成功、衛星通信も視野に」といった記事を読んだら、「中国なんか、再来年の2015には量子通信衛星の打ち上げ目指してるだぜ!?ワイルドだろ~!?」と言ってみよう!
2012-09-12[n年前へ]
■「Cカップのバストなんて実在するわけがない!」ことの数学的証明 
 「真面目に考えてみると、意外に難しくて、意外に面白い」ということがあるものです。たとえ「真面目に考えてみる対象」が「どんなこと」であっても、です。
「真面目に考えてみると、意外に難しくて、意外に面白い」ということがあるものです。たとえ「真面目に考えてみる対象」が「どんなこと」であっても、です。
ブラジャーのカップサイズは、アンダーバストとトップバストの「差」で決まります。「おっぱい解析向けライブラリを書いてみる!? 第1回」で書いた(コーディングした)ような具合で、たとえば、アンダーバストとトップバストの差が5cmならAAAカップ、7.5cmならAAカップ、10cmならAカップ…15cmならCカップ、という具合です。
とても単純に、胸回りの胴体に「球状のバスト」が付いているとすると、カップサイズ=トップバストとアンダーバストの差は「円弧と弦の長さの差分を求めよ」という問題に置き換えることができます。…たとえば、Aカップなら、胸のバストカップ断面に相当する長さ(弦)に10cm足した円弧の形状が、それすなわちAカップのバスト形状だ、という具合です。
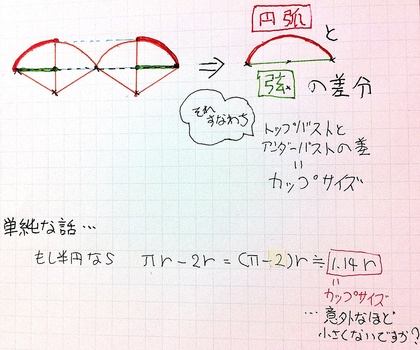
この「円弧と弦の長さの差分を求めよ」問題は、実は意外に難しい問題です。そこで、わかりやすく「もしも、胸が半球形状だったなら」という風に考えてみることにします。つまり、もしも「世界が100人の村だったら」という風に単純化してみるのです。
 もちろん、半球状バストなんて、そんなマルマルとした超立体的バストなんか非現実的ですが、そんな非現実的な立体バストの場合、「円弧と弦の長さの差分=トップバストとアンダーバストの差=カップサイズ」は「(パイ−2)×胸の半径」になります。パイ=円周率は3.14...ですから、「胸の半径に約1.14を掛けたもの」が「トップバストとアンダーバストの差=カップサイズ」に相当するわけです。
もちろん、半球状バストなんて、そんなマルマルとした超立体的バストなんか非現実的ですが、そんな非現実的な立体バストの場合、「円弧と弦の長さの差分=トップバストとアンダーバストの差=カップサイズ」は「(パイ−2)×胸の半径」になります。パイ=円周率は3.14...ですから、「胸の半径に約1.14を掛けたもの」が「トップバストとアンダーバストの差=カップサイズ」に相当するわけです。
自分の胸に手を当てて、じっと考えてみて下さい。あなたの「片胸の幅はせいぜい15cmくらい」ではないでしょうか。ということは、その片胸に半球状バストが張り付いているとすると、その半球状バストの半径は「15cmのさらに半分=7.5cmほど」になります。その7.5cmに1.14を掛けた結果の8.6cm が「トップバストとアンダーバストの差=カップサイズ」で、(トップバストとアンダーバストの差が)7.5cmならAAカップ・10cmならAカップということを思い出せば、(いくらなんでも、それはありえなさそうな)半球状のマルっと超立体な3Dバストですら、カップサイズは(せいぜい)Aカップに過ぎない…ということになるのです。
 超非現実的でありえない「半球状のマルっと超立体な3Dバストでも、Aカップに過ぎない」となると、「アンダーバストとトップバストの差が15cmのCカップ」なんて、そんな物体が果たしてこの世に実在するものでしょうか?バストのカップサイズについて「真面目に考えてみる」と、「そんなもの、Cカップなんてものはありえない・実在するわけがない」…と気づかされるのではないでしょうか。
超非現実的でありえない「半球状のマルっと超立体な3Dバストでも、Aカップに過ぎない」となると、「アンダーバストとトップバストの差が15cmのCカップ」なんて、そんな物体が果たしてこの世に実在するものでしょうか?バストのカップサイズについて「真面目に考えてみる」と、「そんなもの、Cカップなんてものはありえない・実在するわけがない」…と気づかされるのではないでしょうか。
…といったことを「実感」するために書いた検証用「体感コード」を動かしてみたのが、下の動画になります。(アンダーでなく)トップバスト数値と「カップ」の組み合わせでバスト形状を眺めてみるのも面白い、かもしれませんね。(また、この3次元版が「バストとカップサイズからグリグリ・マルマルな立体3Dを眺めてみよう!?」になります)
2012-09-13[n年前へ]
■バストとカップサイズからグリグリ・マルマルな立体3Dを眺めてみよう!? 
 「Cカップのバストなんて実在するわけがない!」ことの数学的証明で、『(おっぱいというか)ブラジャーのカップサイズ=トップバストとアンダーバストの差というものは、少し変数変換すると、それすなわち「円弧と弦の長さの差分を求めよ」という問題に置き換えることができる』といったことを考えてみました。
「Cカップのバストなんて実在するわけがない!」ことの数学的証明で、『(おっぱいというか)ブラジャーのカップサイズ=トップバストとアンダーバストの差というものは、少し変数変換すると、それすなわち「円弧と弦の長さの差分を求めよ」という問題に置き換えることができる』といったことを考えてみました。
「ブラのカップサイズ」イコール「円弧と弦の長さの差分」としてみると、(たとえば)スリーサイズのバスト=トップバストのcmとカップサイズから、バスト形状を求めることができます。…というわけで、トップバストサイズとカップサイズからグリグリ・マルマルな立体3Dな(けれど実に素朴な)オッパイモデルを眺めてみると、それはつまり「こんな感じ」です。
こうして眺めてみると(トップバスト)76のAAAカップという存在は、超巨大な物体に見えてきます。…段ボールと(東急ハンズで買った)発砲スチロールボールで、いつか、1/1スケール模型(つまりは実寸)でも作ってみることにしましょうか。
2012-09-14[n年前へ]
■LED信号機 の「LED配置」は実はとても面白い幾何学だ 
 『LED信号機 の「LED配置」は実はとても面白い幾何学だ』を書きました。
『LED信号機 の「LED配置」は実はとても面白い幾何学だ』を書きました。
たとえば、信号灯の中心に1個LEDを置き、そのLEDを中心として半径rの円を考えてみます。灯内部に変な模様・方向性を持たせないように、縦・横ともにLEDを等間隔に並べるためには、少しの単純化を行うと、(最初のLEDを中心とした)半径rの円上に、距離rおきにn個のLEDを配置すればよい、ということになります。しかし、半径rとなる円の一周長は2πrですから、(距離rおきにn個のLEDを配置するために)その長さ=2πrをrで割ってもその答えは整数にはなりません。それはつまり、同心円上にLEDが等間隔に配置するということは不可能だ、ということです。
2012-09-16[n年前へ]
■「錯覚立体円グラフに(さらに)データ配置マジック」が混ぜられた「Appleが見せたiPadシェア」 
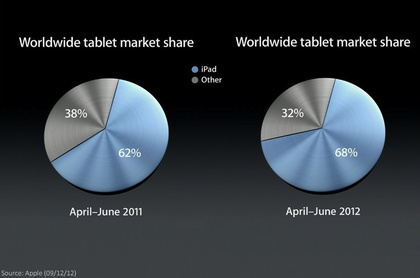 Appleが9月12日に示した「タブレット市場におけるiPadのシェア推移」のグラフ(参考:CHART OF THE DAY: Tim Cook Used These Charts To Make Fun Of Amazon And Google's Tablet Sales)が何だか少し奇妙です(右図)。何がどのように奇妙かというと、円グラフに描かれている「データ系列」が12時の位置からではない、ということが奇妙なのです。
Appleが9月12日に示した「タブレット市場におけるiPadのシェア推移」のグラフ(参考:CHART OF THE DAY: Tim Cook Used These Charts To Make Fun Of Amazon And Google's Tablet Sales)が何だか少し奇妙です(右図)。何がどのように奇妙かというと、円グラフに描かれている「データ系列」が12時の位置からではない、ということが奇妙なのです。
 円グラフを立体的に描き・その立体円グラフを手前から眺めさせることで(遠近感を利用して)、手前にあるデータ系列を大きく(多く)見せる「誇張円グラフ」はよく見かけます。そういった円グラフは(好ましいものではないかもしれませんが)過半数を遙かに超えるものを示す時など、少なからず使われます。しかし、こうした「データ系列」が12時の位置からではなく、1時くらいの位置から始まっている(いるように見せる)グラフは珍しいように思います。
円グラフを立体的に描き・その立体円グラフを手前から眺めさせることで(遠近感を利用して)、手前にあるデータ系列を大きく(多く)見せる「誇張円グラフ」はよく見かけます。そういった円グラフは(好ましいものではないかもしれませんが)過半数を遙かに超えるものを示す時など、少なからず使われます。しかし、こうした「データ系列」が12時の位置からではなく、1時くらいの位置から始まっている(いるように見せる)グラフは珍しいように思います。
ためしに、Appleが使ったスライドの「円グラフ」に真円 と格子線を重ね描いてみたのが下の図です。そうしてみると、この円グラフは、(近くに描かれた)「iPadのシェアを大きく見せる一方で、(遠くに描かれた)「その他」のシェアを小さく見せていることが実感できると思います。さらに、それだけでなく、「データ系列が12時の位置からではなく、1時くらいの位置から始まっている」ことが、「その他」を視点から遠い位置(小さく描かれる領域)へと持って行き、遠近感による(データ比率の)錯覚でiPadのシェアを大きく(2011年から2012年にかけて「その他」が大きく減少しているように)見せることに寄与している、ということがわかります。「自分の視点に近いものを大きく見せ、自分とは遠いものを小さく見せる、という錯覚立体円グラフを最大限に"活用"しているグラフです。

このような「データ配置マジック」を混ぜたプレゼンテーション・グラフは、何というか、”少し新鮮”だったので、「錯覚立体円グラフ」と「データ配置マジック」の効果がわかりやすいよう「図示・可視化」してみました。
2012-09-17[n年前へ]
■(ブラジャー)カップサイズのパラドックスを解き明かせ! 
 ブラジャー・カップサイズのミステリー、あるいはいわゆるひとつのパラドックスに「カップサイズとおっぱいの重さの謎」があります。カップサイズが「(アンダーバストとトップバストの差という)長さ」で決まり、おっぱいの重さ=体積が長さの3乗の次元を持つということから、カップサイズ=アンダーバストとトップバストの差長からおっぱいの重さを求めようとすると、カップサイズが大きくなるにしたがって、おっぱいの重さが信じられないほど重く算出されてしまう…という「オッパイの(ディメンジョンに関する)パラドックス」です。
ブラジャー・カップサイズのミステリー、あるいはいわゆるひとつのパラドックスに「カップサイズとおっぱいの重さの謎」があります。カップサイズが「(アンダーバストとトップバストの差という)長さ」で決まり、おっぱいの重さ=体積が長さの3乗の次元を持つということから、カップサイズ=アンダーバストとトップバストの差長からおっぱいの重さを求めようとすると、カップサイズが大きくなるにしたがって、おっぱいの重さが信じられないほど重く算出されてしまう…という「オッパイの(ディメンジョンに関する)パラドックス」です。
International Journal of Clothing Science and Technologyの挿入図(下図)を眺め、「やはり、そうだったか!」と思いました。この図は、横軸にカップサイズがとられ、縦軸におっぱいの体積(≒重さ)をとり、胸囲違いの「カップサイズ v.s. おっぱい体積」が示されています。この図を見て気づくことは、「カップサイズとおっぱい体積は3次式の関係になっていないどころか、(Cカップより大きいあたりでは)ほとんど線形の対応となっている!」ということです。
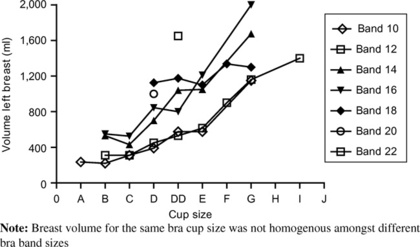
つまり、「カップサイズとおっぱい体積は(3乗の関係でなく)ほぼ比例する」ということが、この図を見るとわかるわけです。
 ブラのカップを算出のためにトップバスト長を計るには「90度の角度で、お辞儀をするスタイル」で計ります(参考:バストの測り方の「定義」と「実態」)。「(ブラジャー)カップサイズ」のパラドックスの謎を解く鍵は、この90度の角度でお辞儀をするスタイルをとっている時のおっぱい変形にあるのかもしれません。
ブラのカップを算出のためにトップバスト長を計るには「90度の角度で、お辞儀をするスタイル」で計ります(参考:バストの測り方の「定義」と「実態」)。「(ブラジャー)カップサイズ」のパラドックスの謎を解く鍵は、この90度の角度でお辞儀をするスタイルをとっている時のおっぱい変形にあるのかもしれません。
たとえば、90度の角度でお辞儀をするスタイルをとっている時は、おっぱい形状が「(底面積がほぼ変わらない)円柱状」になっていると考えたくなります。物体の自然な変形特性を考えれば、下を向いた時、何にも拘束されないおっぱいは垂乳根の母のごとく「下に向かってただ伸びる」ということも自然に起きそうです。
そう考えれば、つまり下を向いたおっぱい形状は「(底面積がほぼ変わらない)円柱状」になっていると考えれば、円柱の体積=底面積×高さですから、「おっぱいの体積は(カップサイズという)長さに単純に比例する関係となる」ということになります。つまり、「オッパイの(ディメンジョンに関する)パラドックス」が消え去ることになるわけです。
ブラジャーのカップサイズという、それほど難しそうに見えないことであっても、少し眺め・考えてみると、実に奥深い問題がたくさん隠れていそうです。
2012-09-18[n年前へ]
■続 (ブラジャー)カップサイズのパラドックスを解き明かせ! - ブラの幾何学 型紙 編 
 「アンダーバストとトップバストの差という長さで定まるカップサイズを基準にすると、おっぱいの重さ=体積はその3乗になっていまうのではないか、つまりは、(カップサイズが大きくなるにしたがって)おっぱいの重さは信じられないほど重く算出されてしまうのではないか…というオッパイの(ディメンジョンに関する)パラドックス
」と解き明かすために(参考:(ブラジャー)カップサイズのパラドックスを解き明かせ!)、裁縫教室で、ブラジャーの「カップ」の作り方(ブラの型紙)を眺めてみました。もちろん、そのココロは「きっとブラジャーのカップが大きくなる度合いは、1/3乗の比例するような具合だろう」という想像と期待を込め、調べてみたのです。
「アンダーバストとトップバストの差という長さで定まるカップサイズを基準にすると、おっぱいの重さ=体積はその3乗になっていまうのではないか、つまりは、(カップサイズが大きくなるにしたがって)おっぱいの重さは信じられないほど重く算出されてしまうのではないか…というオッパイの(ディメンジョンに関する)パラドックス
」と解き明かすために(参考:(ブラジャー)カップサイズのパラドックスを解き明かせ!)、裁縫教室で、ブラジャーの「カップ」の作り方(ブラの型紙)を眺めてみました。もちろん、そのココロは「きっとブラジャーのカップが大きくなる度合いは、1/3乗の比例するような具合だろう」という想像と期待を込め、調べてみたのです。
下の図は、アンダーバスト長違いにおける、カップサイズ(アンダーバスト長とトップバスト長の差 cm)とカップ径 cmの関係を示した結果です。なんと、このブラジャー型紙データは、アンダーバスト長とトップバスト長の差 cmとカップ径 cmは見事に1次の比例関係になっています。…つまり、カップサイズの3乗でおっぱいの体積・重さが増大してしまう、ということになります。
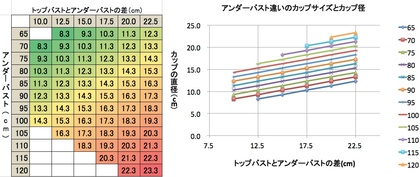
一体全体、おっぱいの大きさ(体積)・重さは、カップサイズに比例するのか・しないのか…一体何乗に比例するのか・しないのか…オッパイの(ディメンジョンに関する)パラドックスは、一朝一夕で解ける問題ではなかったようです。
2012-09-20[n年前へ]
■Microsoft謹製「ペーパークラフト 仮装グッズ・鼻メガネ!」でオフィスの風景を奇妙にしちゃえ!? 
マイクロソフトのPowerPoint用テンプレートから 「ペーパークラフト」を検索し、検索にヒットした中から「(これは面白い!という)大ヒット」が 「ペーパークラフト(仮装グッズ・鼻メガネ)」
(変な髭のガイジンさん風)鼻眼鏡や(謎の貴婦人風)仮面舞踏会な、このパワポで作る仮装グッズは、きっとオフィスで大活躍するはず!

それ以外のテンプレート、「宴会腕章」や「王冠」も、状況次第では役立ちそう!?

2012-09-22[n年前へ]
■PILOTだけが「リフィル多色ボールペンのノックボタンをインク同色」にできるヒミツ!? 
 『PILOTだけが「リフィル多色ボールペンのノックボタンをインク同色」にできるヒミツ!?』を書きました。
『PILOTだけが「リフィル多色ボールペンのノックボタンをインク同色」にできるヒミツ!?』を書きました。
PILOTだけが「リフィル多色ボールペンのノックボタンをインク同色」にできるヒミツは、結局のところ、「PILOT社の多色ボールペンだけが、後端(ペン先とは逆側)から替え芯を入れる構造になっている」ということに尽きます。そして、さらに言えば、PILOT社だけが「その構造の多色ボールペンを作ることができる」のは、その構造が「特許第4689513号」という特許でPILOT社の権利として保護されているからです。
2012-09-23[n年前へ]
■ドラクロワ「民衆を導く自由」の「女神」を姿勢推定して立体的に眺めてみよう!? 
 ドラクロワの「民衆を導く自由(La Liberté guidant le peuple)」に描かれている民衆を導く女性を相手に、人体姿勢推定をしてみました(結果の空間は座標軸が反転してしまっているようですね)。民衆を導く「自由(女神)」の骨格を眺めてみると、力強い上半身とは裏腹に、下半身の方は内股だったりするのが意外です。
ドラクロワの「民衆を導く自由(La Liberté guidant le peuple)」に描かれている民衆を導く女性を相手に、人体姿勢推定をしてみました(結果の空間は座標軸が反転してしまっているようですね)。民衆を導く「自由(女神)」の骨格を眺めてみると、力強い上半身とは裏腹に、下半身の方は内股だったりするのが意外です。
書いたコードが上手くないせいか、時折インド人もビックリの異常関節状態になっていたり、まるで1960年代に流行ったモンキーダンスに夢中になっているかのようにも見えますが、こんな風に有名絵画の世界を立体的に眺めてみるのも、少し面白いのではないでしょうか。

2012-09-24[n年前へ]
■スマートフォンアプリ開発で遊んでみよう!? 
 原稿を書いた「Smartphone-Design-スマートフォンデザイン-~スマートフォンアプリ開発者とデザイナのための総合情報誌」が届きました。
原稿を書いた「Smartphone-Design-スマートフォンデザイン-~スマートフォンアプリ開発者とデザイナのための総合情報誌」が届きました。
たとえば文房具のように、遣う道具・いつも身近に遣う道具は「自分の一部」です。自分の足りないところを補い、そして、自分の力を増幅する道具です。強力な道具を携えると、まるで自分が「何でもできる」ような気がしたりするものです。それは、「速そうな自動車」に乗ると、ブイブイ言わせたくなるのと同じような心地です。
そしてまた、コンピュータ・プログラムというものを始めた頃、「自分が作った手順に沿って機械が動く」ということが、とても新鮮でした。それは、まるで世界を動かす神秘の法則を(自分が)描き・作り出す創物主になったかのような錯覚を生じさせたのです。
そんな勘違いと錯覚を二重に掛け合わせたもの、自分を助ける強力なスマフォを、自分が組んだプログラムで動かし・機能を増やすことができると、あたかも「何でもできる」という気にさせられたりします(たぶん)。
だから、スマートフォンアプリ開発で遊ぶのは、とても楽しそう!と感じたりします。…とそんな駄文を書いてみました。
2012-09-29[n年前へ]
■虹を動画で撮影し、映し出された円形の虹を浮かび上がらせてみよう!? 
 飛行機の下に広がる白雲の上に、丸い虹が見えました。とても小振りですが、綺麗な円が七色に光っています。
飛行機の下に広がる白雲の上に、丸い虹が見えました。とても小振りですが、綺麗な円が七色に光っています。
虹の写真(静止画)をiPhone4で撮ってみましたが、強い明暗を持つコントラスト激しい雲の模様に虹の色が隠れてしまいそうです。だから、虹を写す白雲を動画モードでも撮影し、その動画のフレーム群を平均化することで虹だけを浮かび上がらせてみることにしました。
静止画として撮影した丸い虹が右上で、動画像から画像処理で浮かび上がらせた「虹」が下の画像です。…この画像を眺めると、動画像から平均化処理で浮かび上がらせた虹の映像よりも、普通に静止画モードで撮影した虹の方がずっと綺麗に鮮明・カラフルに見えます。

今回は(も?)工夫をしてみたものの、その工夫は役に立たずに終わってしまいました。…しかし、思いつきや工夫を止めたら進歩はない!人間が猿と(少しだけ違うのは)そんな工夫を思い切り深追いしたことだっ!というわけで、そんなこんなの役立たずネタは、これに懲りずに、まだまだ続きます。
2012-09-30[n年前へ]
■”未来っぽい”セグウェイ風電動三輪車は最高だ!? 
 セグウェイ風電動三輪車に乗った警備員たちが、人混みの中を巡回していました。そのセグウェイ風の乗り物は、まるでセグウェイであるかのように見えるくらいですから、前輪と後2輪の間の距離=ホイールベースが非常に短く、「投影面積(フットプリント)」は人のそれとほとんど変わりません。そんな利点を活用し、私たちが人を避けて歩くのと同じように、混雑する中をヒョイヒョイ進んでいきます。
セグウェイ風電動三輪車に乗った警備員たちが、人混みの中を巡回していました。そのセグウェイ風の乗り物は、まるでセグウェイであるかのように見えるくらいですから、前輪と後2輪の間の距離=ホイールベースが非常に短く、「投影面積(フットプリント)」は人のそれとほとんど変わりません。そんな利点を活用し、私たちが人を避けて歩くのと同じように、混雑する中をヒョイヒョイ進んでいきます。
 そのセグウェイ風電動三輪車の構造は、モータ内蔵の電動自転車用タイヤが付けられているだけで、いたって普通の電動自転車です。「投影面積(フットプリント)が小さい」というセグウェイの利点のひとつは、複雑な技術を使わなくても、町にあふれる既存の安い部品でこんな風に組み立てることができるんだな、とちょっと新鮮に感じます。
そのセグウェイ風電動三輪車の構造は、モータ内蔵の電動自転車用タイヤが付けられているだけで、いたって普通の電動自転車です。「投影面積(フットプリント)が小さい」というセグウェイの利点のひとつは、複雑な技術を使わなくても、町にあふれる既存の安い部品でこんな風に組み立てることができるんだな、とちょっと新鮮に感じます。
このセグウェイ風電動三輪車、ハンドルには前カゴも付いていて買い物にも便利そうですし、詰めて乗れば二人乗りも(頑張れば3人乗りくらいも)できそうな感じです。そして、フットプリントが小さいので駐輪スペースも最小で済みます。
この”セグウェイ風”電動三輪車は「未来の乗り物」ではないかもしれませんが、安っぽくもほんの少し”未来風”な乗り物です。そんな、バッタもんな未来を眺めていると「未来を作るやり方は色々なんだなぁ」と楽しく感じます。































