2012-11-01[n年前へ]
■iPad上で使うLua言語プログラミング環境Codeaでネイティブ・アプリを作ってみよう!? 
Lua言語を使いiPadアプリをとてもお手軽に作成することができるCodea(Codify)がランタイムライブラリを使うことでApp Storeに出せるネイティブアプリを作成できるようになったということで、その手順を確認してみました。
Codeaのランタイム・ライブラリをダウンロードすると、その中にXcodeプロジェクトを作成するシェルスクリプト（make_project.sh）があります。そこで、
make_project.sh hogeとタイプして、Xcodeプロジェクトと必要なファイル群を生成します。エミュレータで動かすのなら関係ありませんが、このhogeはアプリケーションのBundle Identifier にも使われます。
その後、Xcodeプロジェクトを開き、ClassesからProject.codeaを削除した上で、（iExploerなどで）iPad内のCodeaディレクトリ内から（ネイティブ・ビルドしたい）プロジェクトファイルをOSX側にコピーした上で、プロジェクトファイルをProject.codeaとリネームして、XcodeのClasessフォルダに（フォルダー・リファレンスを行わせた上で）コピーします。つまり、単にデフォルトのProject.cocoaを（ネイティブ・ビルドしたい）プロジェクトファイルで入れ替えます。
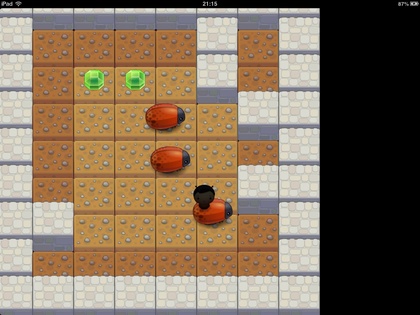あとは、ターゲットを選んだ上でビルドすると…ターゲット上でCodeaネイティブ・アプリが転送され、走り始めます。たとえば、右のスクリーンショットはiPad2でサンプルのゲーム・コードをネイティブビルド＆実行してみたところです。
Lua言語でproce55ingのAPIを参考にして作られている…というCodea環境をいじってみたくなる人も多いに違いない…というわけで、Codeaでネイティブ・アプリを作る手順を実際に追いかけてみました。
2012-11-02[n年前へ]
■「歩くべき or 走るべき？の境界線」は時速８ｋｍだ！
『「歩くべき or 走るべき？の境界線」は時速８ｋｍだ！』を書きました。
だから、もしも「歩くべきか、それとも、走るべきか…？」とハムレットが悩んでいたとしたら、「それはキミ、歩くと走るの境界線は時速８ｋｍだよ」と教えてあげれば良い、ということになります。
人は「自然」から生まれているわけですから、人がどのように動くのかということを考えようとしたら、たとえば人が行うことを模倣しようとする機械やロボットを作ろうとしたら、何が自然かと言うことを眺めてみてみれば…その答が自ずと見えてくることもあるかもしれません。
今日は、「歩くべき or 走るべき？という境界線」を、「自然」の観点から眺めてみました。
2012-11-04[n年前へ]
■日本シリーズの”疑惑の危険球”を画像解析してみよう!? 第1回
日本シリーズ第５戦（日本ハム vs. 読売ジャイアンツ）で「危険球とすべきか否か」の判断が分かれたというニュースを見て、「近未来の日本シリーズ放映なら、こんなシーンの直後には、ピッチャーが投げたボールコースを立体的に実感・体感できる”プレイバック・シーン”が即座に再生リピートされているに違いない」と考えました。
たとえば、ボールの軌跡を、ピッチャーの視点から・キャッチャーマスクの内側から・あるいは、バットを手にしたバッターの視点から…投げられたボールの軌跡を３６０°周囲の世界からレンダリングしているに違いないと思います。
今日は、日本シリーズ第５戦の「疑惑のボール」の軌跡を画像合成して眺めてみました。もちろん、そのボールの軌跡は、シンプル過ぎるくらいの単純な放物線を描いています。そういった、ボールの軌跡形状や、（進行方向が変化しても）速度の時間変化は滑らかで小さい…といった、ごく単純で当たり前の物理制約条件を活用すれば、（たとえ一箇所の定点TVカメラから撮影したとしても）ボール軌跡を立体的に再現できるように思われます。…というわけで、今日は、（続 パノラマ画像で眺める「巨人阿倍の空中バウンド・ホームラン」の秘密!?で書いたMathematicaコードを流用して）「（2012年 日本シリーズ第５戦の）疑惑の危険球」をまずは眺めてみました。
2012-11-05[n年前へ]
■日常生活で役立つ数学の問題「マンション駐輪場割り当て数の将来予測」編
マンションの理事会や管理委員の役職番が回ってきたりすると、マンションの駐輪場の「割り当て数」について頭を悩ませたりすることがあります。たとえば、面積が限られているスペースに、自転車置き場とオートバイ置き場を作らねばならない…けれど、その比率は一体どのようにしたら良いかわからない…といったこともあると思います。
あなたが住んでいるマンションが、１００戸入居できる新築マンションで、けれどまだ10世帯しか入居しておらず、その入居済み10世帯の中でオートバイを持っているのは１世帯でたった１台だけだったとします。
残り90戸の入居がまだ行われていない現時点で、「バイク置き場」の個数を決めてしまわなければならないとしたら、あなたは一体何台程度バイクを置くことができるようにしたら良いものでしょうか？
「世帯はバイクを１台しか持つことはない」ものとして、"10世帯の中でオートバイを持っているのは「1世帯たった１台」だけだった"ということをもとにして、世帯がバイクを持つ確率pの（さらに）確率分布を(逆算して)求めてみたのが下のグラフです。
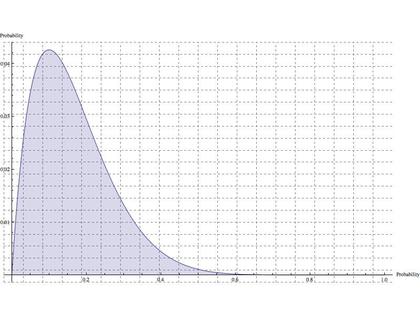
このグラフを眺めてみると、各戸がバイクを持っている確率としては、「確率が一番高いのは1/10程度だけれども、バイクを持つ確率は、それより実は結構高いのかもね」という具合になっています。そして、バイクを持つ確率が上のグラフのような場合に、さらに「100戸全て入居済みになった時点でのバイク保有数予測」をしてみたのが次(下)のグラフです。
10戸入居時点でバイクが１台だけだったから、全部で100戸のマンションならトータル１０台のバイク置き場を用意しておけばいいかなと思ったら…わっ！バイク置き場が全然足りない事態になってしまった ！？と冷や汗をかくことになりそうです。
日常生活の中では、こんな「ご近所さんの間ですったもんだしがちな割り当て数に関する難問題」に出会うことも頻繁にありそうな気がします。…なんていう風に考え出すと、あぁ学校の勉強をもっと真面目にやっておけば良かった…（泣）と思ったりしそう、です。
2012-11-07[n年前へ]
■「答えられる（だけの）力」は必要ない
「やりたいこと」はあるけれど、そのやりたいことを的確に表現する「コード」を書いたなら、（機械でない）人に頼む仕事自体が消え失せてしまうというジレンマがあります（未来に生き残る職業は「プログラミング言語・環境開発者」と「ニッチで・けれど高価なものを作る人」）
それと同じように、的確な「問い・質問・問題」を一度作ったならば、その「問い」に対し（機械以外の）何かに答えてもらう必要はほぼ消え失せてしまう、というジレンマもあります。なぜかというと、的確な「問い」というものは、「答えると意味あることを、答えうる範囲・解きうる条件に落とし込む」ものであって、そのような「問題」を描き出してしまったならば、当たり前のように、その「問題」の答えは導き出されるものだからです。
だから、「やりたいこと」を的確に表現したならば、（後は機械に任せれば）やりたいことが消えてしまうように、「解くべき問題」を的確に表現し得たなら「問題を解くための作業」の過半数は終了しているというようになることも多いような気がします
本当のところ、「答える」ためには「的確な問い」を描くということが必要十分条件なのではないか、と思います。だから、「問題を出されたら、答えることができる能力」なんて（その問題が作り出された段階で、すでに問題は解かれているのですから）実は無意味だ…と感じることも多いのです。
必要なのは「問い・問題」を手にするための力で、「答えられる（だけの）力」ではないだろう…と思うことが多くなりました。
人間は、決してあきらめてはならない。
「ロボット (R.U.R)」 カレル・チャペック
2012-11-08[n年前へ]
■続 「メガネをとると美人になる」現象の秘密 ~「”サイズが違う近視用メガネ”のブサイク化マジック」編
『続 「メガネをとると美人になる」現象の秘密 ~「”サイズが違う近視用メガネ”のブサイク化マジック」編』を書きました。
しかし、「メガネをとると美人になる」現象の秘密は、実はこれだけではありません。
サイズが合わない近視用のメガネを掛けていると、目の間隔が妙に離れて平目顔に（外見上）見えてしまったり・目の感覚が過剰に狭まってプロポーションが悪いブサイク顔に見えてしまう…という現象もさらに起きてしまいます。
近視用メガネをかけた人を眺めると、メガネレンズの内側にあるものが「小さく」縮小されて見えるのですが、縮小される時の中心位置はレンズ中心位置となります。すると、目の位置とレンズ中心位置が一致していないと、目が縮小されて見えるのと同時に、目の位置も移動して見えてしまうのです。
2012-11-13[n年前へ]
■「”ライト内蔵型”眼帯」があれば「見えないもの」も見えてくる!?
数日前から「片目」生活をしています。右目は眼帯で覆い、目の前の景色を見ることができるのは「左目だけ」という状態です。だから、ゴルゴ１３ではありませんが、「（後ろならぬ体の右側がほぼ見えないので）オレの右側には立つな」という気分です。
そんな片目眼帯生活の中で気づいたことは、眼帯越しに「明るさ」を感じることさえできれば、驚くべきことに「立体感」を感じるということでした。たとえば、目の前にいる人の姿は（左目から見える）左側しか見えていないはずなのに、（眼帯越しに右目が”明るさ”を感じさえすれば）不思議に両側から眺めている心地になるのです
（眼帯に覆われた）右目を完全に手で覆ったりして明るさを感じない状態にすると、「見えている景色」は平面的で”単なる画像”にしか思えないのですが、ひとたび右目が明るさを感じた途端、目の前の景色が立体的で確かな広がりを持っているように感じます。
どうやら、眼帯に覆われた目が（もしも眼帯がなかったら）見ることができる景色を、脳のどこかの回路が勝手にレンダリング補完しているようです。その回路は、眼帯に覆われて目の前を見ることができない目に信号が入ることで電源が入るようです。たとえ、その信号が何の情報もない一様な明るさだけであったとしても、その回路は動き出すようです。
それだけでなく、その映像補完＆立体感生成回路と同じように、視界からの文字認識やパターン認識といった画像処理回路も、見えない右目に光信号が入ることで（その右目からの情報が完全に無意味なものであったとしても）どうやら処理能力がアップするようです。たとえば、「ウォーリーを探せ」を試しにやってみたところ、右目を完全に遮光していると「絵本のページからウォーリーを探し出す」のは至難の業に思えます。しかし、眼帯越しの右目に明かりを当てた状態だと、結構簡単にウォーリー模様を見つけ出すことができるのです。
「”ライト内蔵型”眼帯」があると、とても便利なのではないかと考えます。たとえ瞼を閉じて・眼帯で覆っている（つまり目に優しい）状態であっても、眼帯に内蔵されたライトで目に明るさを感じさせることができたなら、立体感（遠近感）も感じることができるし・文字／パターン認識能力も向上させることができるかもしれない、と思ったのです。
というわけで、100円ショップで超小型ライトを買い、マイ眼帯のガーゼに埋め込んでみました。これで、瞼越しに光を網膜に当てて、脳内画像補完システムで立体感と画像処理能力をアップさせることができるはずです。「眼帯を奇妙に光らせる不審者」として怪しまれなければいいな…と願いつつ。
2012-11-14[n年前へ]
■「iPad miniキーボード実寸PDF」を作ってみた
iPad miniが欲しいけれど、ソフト・キーボードの大きさが小さくなって果たして実用的に使うことができるかが気になる…というわけでiPad miniキーボードの実寸PDFを作ってみました。このPDFをプリンタで出力すれば（あるいはセブンイレブンでコンビニプリントすれば）、iPad miniのキーボードを打つ感覚を実感することができます。
紙上にプリントアウトされたキーボードでは、押しても感触を得ることはできませんが、それは本家本元iPad miniのキーｰボードだって同じです。だから、このペーパー・キーボードを叩き、あなたの手のサイズで打鍵感覚を確かめてみるのはいかがでしょうか。
2012-11-16[n年前へ]
■検証！「夏目アナの脇汗事故はなぜ起こったか？」ー灰色の服が汗染みに弱い理由
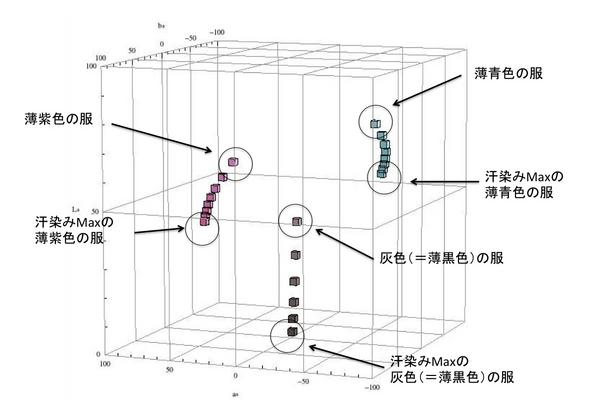『検証！「夏目アナの脇汗事故はなぜ起こったか？」ー灰色の服が汗染みに弱い理由』を書きました。
「汗染みの目立ちやすさ」は、「白＋（繊維本来の）○×色」と「（繊維本来の）○×色」の差が一番大きな色は何色か？という問題に置き換わります。 そして、白と最も違う色は…「そうだ黒に違いない！」ということにも気づくのではないでしょうか。 つまり、「白色に黒を混ぜた色＝灰色（グレー）」の服が「一番汗染みが目立つ色」なのだろう、と思い至るはずです。
ちなみに、「鮮やかな色」の服の方が汗染みは目立ちませんから、汗染みができそうな場合には、そうした色を選んでおくのがコツかもしれません。
この解析で使った（作った）ライブラリやスクリプトは「Mathematica 色処理ライブラリを更新しました」を参考にして下さい。
2012-11-18[n年前へ]
■「黒パンツを覆う白生地中の光収支方程式」問題をエクセルで解いてみよう!?
検証！「夏目アナの脇汗事故はなぜ起こったか？」ー灰色の服が汗染みに弱い理由では、脇汗をかいた時、着衣の外見がどのような色になるかを考えてみました。
今日は、別の着衣の「外見色」問題、「白生地で覆われた黒パンツは一体どんな風に見えるのか？」という（いわゆるひとつの）「黒パンツを覆う白生地中の光収支方程式」問題を、表計算ソフトであるエクセルを使って解いてみることにします。
「白い生地」は光を散乱／拡散させる素材です。 簡単のために、白生地が完全に光を散乱／拡散させるものと近似すると、生地中の微小領域（部分）を考えれば、その領域は周囲に等方に光を発するということになります。 逆に言うと、「白生地の各領域は周りから発せられる光を受ける」ということです。 そんな風に考えると、（下図に描いたように）白生地の各領域の輝度は、「周囲の輝度の平均」を用いた形の式で表されることもわかります。つまり、この「黒パンツを覆う白生地中の光収支（輸送）方程式」は熱伝導方程式などを解いたのと同じやり方、エクセルで「反復計算（循環参照計算）」を使えば解くことができるのです（下図参照）。
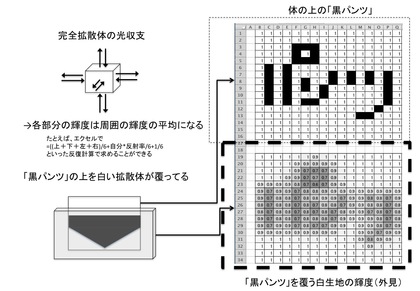
それでは、実際にエクセルを使って「白生地で覆われた黒パンツは一体どんな風に見えるのか？」問題、すなわち、「黒パンツを覆う白生地中の光収支方程式」問題を解いてみることにします。（参考までに、今回作ったエクセルのファイルはここに置いておきます）
まずは、エクセルに『体の上の「黒パンツ」』を示す「反射率分布」を白黒（1,0）で造ってみます（上図のA1からQ16までの領域）。
そして、その下に（B19からQ34までの領域）に「（黒パンツを覆う）白生地」を作ります。
白生地の各領域には "=（上＋下＋左＋右）/6 + 自分×反射率/6+1/6" といったような式を入力します。
そして「反復再計算」を実行すると「白生地で覆われた黒パンツは一体どんな風に見えるのか？」をエクセルが計算してくれるわけです。
また、「数値の大小が色を表すような書式」にしておけば、計算結果をそのまま濃淡のイメージとして眺めることもできます。
さて、体の上に「黒パンツ」があるとして（上図の右上部分）、その「黒パンツ」を覆う白生地が（外見上）どんな輝度に見えるかの計算結果を示したのが、上図の右下部分です。
（白=1, 黒=0）という色で示した計算結果を眺めてみると、白生地越しの黒パンツはずいぶん「ぼやけた姿」となって見える、ということがわかります。
単純な計算ですが「確かにそんな感じ」という結果になりました。
下着が透けてしまう・それとも大丈夫（透けない）といった「着こなし」の問題に悩んだときは、その問題を表計算ソフト・エクセルを使って「実際に解いてみる」という解決策はいかがでしょうか？
2012-11-19[n年前へ]
■送電線を伝う人たちが描き出す「青空上の五線譜」
蒼い冬の空を背景にして、送電線を何人もの人たちが伝い電気工事をしていました。その風景は、まるで五線譜の上にト音記号を記して、オタマジャクシならぬ音符が美しいメロディを描いている…そんな風に見えます。
蒼く染まった空の下を、地上数十メートルの高さを、高圧線にぶら下がりながら鉄塔の間を移動するのは、一体どんな心地なのでしょうか。遙か遠くの発電所から、山を越えて谷を越え、何百ｋｍもの旅をして、あなたの部屋まで届く電線にぶらさがって、鉄塔の間を少しづつ動いている人たちがいます。
高いところが好きな人なら限りなくキモチ良く、高所恐怖症の人たちにはガタガタブルブルな…けれど何だか素晴らしく幻想的な「青空上の五線譜」が今日見た景色です。
2012-11-20[n年前へ]
■Wondernotes記事ピックアップ（2011.11~2012.11）
１年くらい前から、週刊から隔週くらいのペースで「Wondernotes」に記事を書いてきました。というわけで、１年間に書いた中から、いくつかをピックアップしてみました。自サイトで書くものとは、少しだけ趣が違うような・けれどほとんど変わらないような…そんな十数個の記事をピックアップしてみました。
■「ミニスカ・スリーサイズ・メガネ女子」の秘密：
- 建築基準法とミニスカートの幾何学による「３５ｃｍ丈のミニスカートは絶対安全」という証明
- 女性タレントの法則「”8″が付いてるスリーサイズはかなりウソ」
- 続 「メガネをとると美人になる」現象の秘密 ~「”サイズが違う近視用メガネ”のブサイク化マジック」編
■「マンガ」の秘密：
- アメコミ・ヒーローの「色使いのヒミツ」を調査せよ！
- 「教室の黒板を夕日が照らす」のは「マンガの中だけの話」です!?
- 「美術室の黒板」は「夕日に照らされる向き」に作られる!?
- ゴルゴ１３は「ライフル弾の品質管理」に実は意外と甘かった!?
「決まり」の秘密：
■「信号機」の秘密：
■「商品」の秘密：
■「時代」「TV」の秘密：
2012-11-21[n年前へ]
■「北海道は果たして日本固有の領土なのか？」「大戦後の日本分割統治案に沿っていたら日本を支配する国々は？」
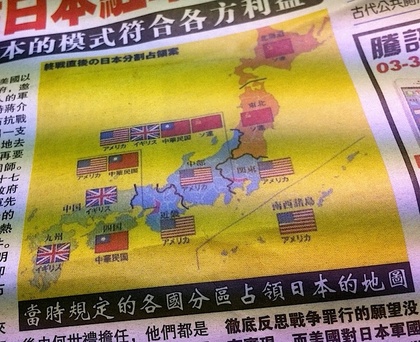
中華料理屋で「ご自由にお持ち下さい」という張り紙と共に無料で配られている「網博週報」という週刊新聞を、毎週楽しく読んでいます。中国視点の記事が、とても新鮮だからです。
最近は、「北海道は果たして日本固有の領土なのか？（戦国時代に遡ってみれば、そもそも北海道は日本の領土と言えるのか？）」「第二次大戦終直後の日本分割統治案に沿っていたなら、日本の各地域はどの国が統治する？（どの地域を各国・中国が統治しているのか？）」というシリーズが面白いです。なるほど、東京・大阪という２大都市は、複数の国による統治になっていたり、なぜか四国は中国統治だったりしたのか…と「日本の歴史再入門」といった具合です。
2012-11-22[n年前へ]
■iPad mini用「究極・至高のノート」キットを作ってみた！
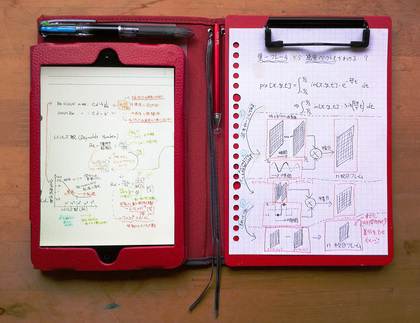iPad mini用の、（今手に入る限りの道具を使った）「究極・至高のノート」キットを作ってみました。ここで言う「究極・至高のノート」というのは、人の苦手なことを最大限に補い、そして人の得意なことを最大限後押ししてくれる、そんな道具です。
作ったのは「頭に浮かんだことを紙に”手書き”するクリップボードを（利き腕側の）右に配置し、書いたノートや本をすべて格納してあるiPad miniを左に配置した超コンパクトな”ノート”ケース」です。
材料費3000円ナリで作った”ノート”を広げれば、「忘れてしまいがちな過去に自分が思いついたこと」や「覚えようと思っても記憶することができない書籍に書かれている内容」には、（iPad miniが担う）左頁を介して自由にアクセスすることができます。
そして、自分の頭が思いついた曖昧で電子化しづらい限りなくアナログでとりとめもないことは、右頁の紙上に描くことで、何かしらの形にしていくことができます。
つまり、「人の苦手なこと＝記憶すること」を最大限に補い（記憶が苦手なのは私だけ…ではないですよね？）、そして「人の得意なこと＝何かしらの新しいことを作り出すこと」を最大限後押ししてくれる”ノート”です（新しいことを作り出さず・繰り返すだけなら機械やロボットには勝てないですし…）。
もちろんこの”ノート”は、ひとたび折り畳めば、容積を無駄にすることのない薄型コンパクト・サイズになります。人の苦手を補い・得意を後押する「いつでも寄り添うノートブック」は、今日この瞬間に（安く）手に入るものとしては、まさに究極・至高のノートです。
この”ノート”の便利さが実に素晴らしいので、何十個か複製し・布教に廻りたい今日この頃です。右利きの人なら私が作ったのと同じような配置で作り、左利きの人であれば左右逆に作る、…他の誰でもない自分自身のための「自分の苦手を補って・自分の得意にエールを送る」そんな道具を作ってみるのはいかがでしょうか。
2012-11-23[n年前へ]
■日本語を読むための「必要最低解像度」は少なくとも200PPI以上です
「iPad mini用「究極・至高のノート」キットを作ってみた！」と書きましたが、それは「今手に入る・かつ安く手に入る道具でできる限りの範囲で最善」だというだけの意味で、決して「それでもう十分・満足だ」という意味ではありません。
たとえば、iPad mini の解像度は、日本語書籍を読むには不十分です。ここでいう「不十分」は主観的な感想の話ではありません。なぜなら、iPad miniのディスプレイ解像度163PPI程度という数字は、日本語の書籍を表示するのは原理的に不十分なものだからです。
日本語の書籍には、おおよそ6ポイント（あるいは8級程度）よりも大きい文字が使われます。たとえば、６ポイント文字なら縦横が２mmより少し大きいくらいの文字サイズです。9ポイントなら文字サイズは３mm四方程度となります。
そんな大きさの文字をディスプレイで表示したとき、一体「何ピクセル四方になるのか？」を示したのが下のグラフです。言い換えれば、ディスプレイの解像度に応じて「所定の大きさの文字をどのくらいのピクセルで表示することができるのか」を示したグラフです。
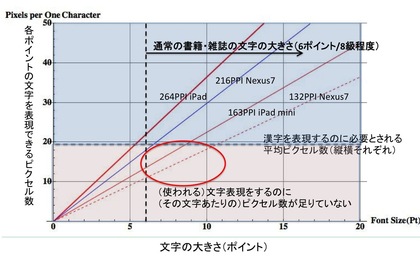
日本語の漢字は、平均すると12画程度の画数になります。そして、「（人が読む）文字」は（しかも文字の中でも特に漢字という文字は）、線が縦横同じように・等間隔に並ぶことが多いという性質があります。なぜなら、そういう状態が一番「人が読みやすい」状態だからです。その結果、大雑把に言うと、平均１２画なら、縦横の線はそれぞれ約６本程度存在する、ということになります。
すると、２次元平面上において、縦横各軸に対して（１文字の大きさの中に）６本程度の線が等間隔に存在するということは、それらの線を表現するためには、１文字を縦横が最低１２ピクセル以上で構成されていなければなりません。もちろん、それは「最低必要とされるピクセル」の話であって、文字の中で線が引かれる場所（位相）・幅によっては、最低20~数十ピクセルが必要とされることになります。
そこで、冒頭に示したグラフ「（ディスプレイの解像度に依存して）所定の大きさの文字をどのくらいのピクセルで表示することができるのか」を眺めると、200PPI以下の解像度の場合には、日本語書籍で使われる大きさの文字を表現するには解像度が不足している（１文字をたかだか十数ピクセル四方で表現することになってしまう）ことがわかります。
つまり、たとえばiPad miniの163PPIといった解像度程度では、日本語の書籍に使われる文字を（日本語の書籍で使われるのと同じような大きさで）表現することはできないのです。アルファベット文化圏であればともかく、漢字を使う日本語書籍を読む限りにおいては、200PPIといった解像度では「最低解像度（にまだ足りない程度の解像度）」と読み替えなければならない数字なのです。
解像度が足りているか・不足しているのかを考える時は、「出力しなければならないパターン」を原理的に出しうるかを、まずは考えてみると良いような気がします。その上で、日本語書籍で使われる「パターン」を再現するためには、200PPI程度では不十分だ…というのが現実です。
2012-11-24[n年前へ]
■横浜「関内」を（かつて日本国内＝関外と隔ていた）関所跡に行ってみた。
『横浜「関内」を（かつて日本国内＝関外と隔ていた）関所跡に行ってみた。』を書きました。
約150年前の頃には、この橋の海側には世界へと続く道があり、山側には江戸から明治そして大正へと進む日本が広がっていました。今日は、横浜関内と日本国内＝関外とを隔ていた関所跡に行ってみました。
2012-11-25[n年前へ]
■「折る刃」式カッターが「最初だけ長持ちする」理由!?
「（いわゆる刃先を折ることができる方式の）カッターで何枚紙を切ることができるだろう…？」という疑問が、ふと頭に浮かびました。そこで、（切れ具合を意識し・同時に刃先を顕微鏡で確認しつつ）NTカッターでひたすら紙を切って、その疑問の答えを確かめてみることにしました。
まずは、スタート時点のカッター刃先を顕微鏡で撮影したのが、右の写真です。まるでルパン三世の石川五ェ門が手に持つ日本刀「斬鉄剣」のように黒光りしています。
「カッターの刃で何枚紙を切ることができるか?!」実験を開始すると、120枚（「生体内熱移動現象」）・180枚（「電磁気」）・130枚（「日本文学史」）…と順調に紙（本）を裁断していくと、４冊目（「JavaScriptハッカーズ・プログラミング」）の50枚目に達したところで、切れ具合がどうにも悪くなりました。つまり、480枚の紙を切ったところで「（１回目の）ギブアップ」となりました。
さて、（刃先を折って）刃先を新しくして、装いも新たに裁断作業を始めると、なんと６５枚切ったところで早くも切れ味の悪さを感じるようになってしまいました。…そこで刃先を観察してみたのが下左の写真です。拡大して眺めてみると、刃先が折れてしまっていることがわかります。（右下の写真は、刃先をさらに交換した後の刃先拡大写真です）
そこで、欠けてしまった刃先を折り、まっさらで新しい刃先にした上で、さらに紙を切る作業を続けます。すると75枚切ったところで、またしても切れ味の悪さを強く感じるようになりました。そこで、刃先を交換することにして、その時の刃先が下の写真です（左：切れ味が悪くなった状態、右：刃先を折って刃先を新しくした状態）
…というように、実験（裁断）作業を続けていると、「刃を折ることで（新しい）刃先を出した状態」では「刃先が折れやすいのではないか？」という印象を受けました。それを逆に言えば、一番最初の先端刃は比較的刃先が折れにくいようだ…という印象です。最初の刃先は数百枚の裁断作業に耐えることができるけれど、次からの刃先は百枚程度の裁断を行うと刃先が折れてしまいがちなのかもしれない？…と感じるのです。
構造的な原因か、あるいは刃を折る際の何かが影響しているのか…折る刃式カッターの秘密を探る実験、まだまだその実験の旅は続きます。（続く）
2012-11-26[n年前へ]
■ブラウザ上で動く動的数式オブジェクトソフトで「女の子」周りの視線を眺めてみよう!?
数値計算および動的描画ソフトウェアというような具合の（つまりはどのようなソフトウェアであるかを表現しづらい） GeoGebraというソフトがあります。数式を入れると、その数式に対応するオブジェクトが表示され（数式を変更するとそれに応じてオブジェクトも変形し）、オブジェクトを移動、変形させると数式も自動的に変更される…というソフトウェアです。
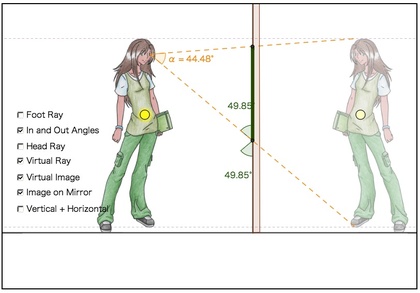このGeoGebraは、iPad やAndroid 版の開発も進められています。そして、それと同時にHTML 5のブラウザ上で動くWEB版も開発されています。このWEB版GeoGebraにアクセスすると、アニメかマンガのヒロインみたいな女の子周りの視線計算をすることができます。
描き出されること自体はごく当たり前の「幾何学」であったとしても、その幾何学が描くキャラクターが格好いい女の子！となると、意外なほどに目を惹き・面白く感じてしまうものです。
GeoGebraのようなオブジェクトと数式を動的に連係して動かすことができる（そして、その数式やオブジェクトで示された関係を理解することができる）ソフトの使い道は、ちょうど「ミニスカートの幾何学」カリキュレータや数学ソフトウェア Geo Gebra でハロー・オッパイ！のように、「目や心を惹く何か」を数式で描き出し、それを動的に動かしてみる…という世界が似つかわしいのかもしれません。
「ミニスカートの幾何学」カリキュレータを作ってみました。どういうものかというと、「ミニスカートの幾何学～32cmの攻防戦～」の計算をユーザがグラフィカル・ユーザーインターフェースを使って自由に行うことができるものです。具体的には、「階段の角度」や「スカートの長さ」を自由に変えて、ミニスカートの幾何学を勉強することができる、というものです。
「ミニスカートの幾何学」カリキュレータ
この動画は、オッパイの表面（境界）の各部分にかかる力を元に、張力を計算し、張力を曲率に（テキトーに）換算を行った上で、曲率＝２階微分値を２階積分した結果をGeo Gebra でインタラクティブに図示した図を（大雑把に言えば）、パラメータを適当に動かすことでアニメーションにする…という具合で作られています。
数学ソフトウェア Geo Gebra でハロー・オッパイ！
2012-11-29[n年前へ]
■「オシッコが捻れて見える」のは尿道の異方性と表面張力が原因だ!?
寒くなってくると、自然とトイレが近くなってきます。
一日になんども、「放水作業」をするようになると、「オシッコが空中で描き出す形状」が気になり始めました。
たとえば、オシッコの放水速度が低いときには、（右上写真のような）捻れた輪ゴムのような形状になっているように見えます。
そして、ひとたびオシッコの速度が増してくると、捻れた輪ゴムのような形だったはずのオシッコが、グ~ンと長~く伸びた形状に姿を変えます（右図参照）。とはいえ、そんな風にオシッコの捻れの周期は変わると言っても、オシッコの姿は結局のところ、トルネードというかスクリューのように、グルグルと捻れた姿であることには変わりありません。
…この「おしっこ」の捻れ形状は一体どのようにして生まれているのでしょうか？そんな、ことを考えて、メモ書きしてみたのが下の写真です。
「おしっこの放水口」の断面は、完全な円ではありません。少なくとも、…いや大幅に扁平・潰れた形状になっているように思います。その扁平形状に、さらに放出時の速度異方性が加わって、おしっこは大きく潰れた楕円状の断面となり、尿道から空中に飛び出ていきます。
さらに、その楕円状のオシッコが表面張力に導かれるまま、楕円形状の「引き延ばされた部分と縮んだ部分」を交互に入れ替えることで（それに初期の異方性が加わることで）、あたかもオシッコがスクリュー＆トルネードのごろとく捻れ進んでいくように見えるのではないだろうか、と考えたのです。
そんなわけで、トイレに行くたび観察を続けているのですが、まさか「普通の放出口は完全円形なのが普通で、オシッコがトルネード形状に見えるのは異常」という「意外な真実」が隠れていたりしないだろうか…と、そんな恐怖に小便をし終わった後、ひとりブルってみたりするのです。
2012-11-30[n年前へ]
■発表ほやほや Mathematica 9.0 の新機能 でハローおっぱい
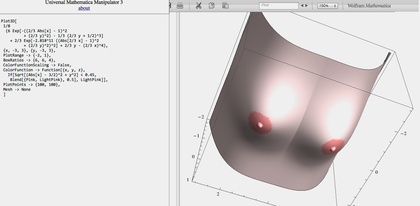数式処理/プログラミング言語（環境）のMathematicaの新バージョン9.0（英語版）が登場しました。新しい環境が（言語）が出たら、まずはHelloWorldを書いて使ってみよう！ということで、いつものように「ハローおっぱい」を書いてみました（生まれたての赤ちゃんが一番最初に見る世界は、それすなわちおっぱいですから）。
Mathematica 9.0の新機能のひとつに「３次元格子点データをボリュームレンダリングすることができる」というものがあります。そこで、Mathematica版「おっぱい（曲面）方程式」で「あなた好みのおっぱい」を作る!?で描いた「おっぱい（曲面）方程式」（右上画像）を、今日はボリュームレンダリングで描いてみました。つまり、おっぱいのボリューム＝”塊”方程式として描いてみたのが、下の画像です。
今回は、以前の関数をそのまま使いましたが、ボリュームレンダリングらしさを活用するならば、一体どんな「可視化」をすると面白いでしょうね…？
」など。