2013-02-03[n年前へ]
■歴代 iPhone / iPad カメラの赤外線感度を横並びで調べてみた 
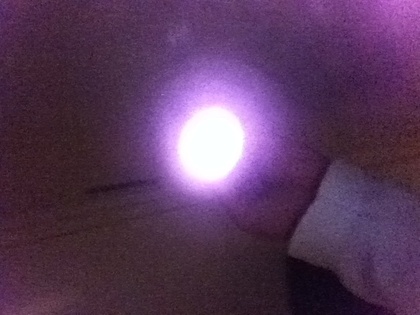 163円で「赤外線LEDライト」を作ったので、赤外線LEDライトを持ちって街に繰り出して、歴代iPhoneとiPadの「メイン(背面)カメラ」と「フロント(Face)カメラ」の赤外線感度を調べてみました。「同じ基準」で横並びに比べ、赤外線が写る・写らないを評価してみたのが下の○×表です。(参考:iPhoneに搭載されたカメラモジュール一覧)
163円で「赤外線LEDライト」を作ったので、赤外線LEDライトを持ちって街に繰り出して、歴代iPhoneとiPadの「メイン(背面)カメラ」と「フロント(Face)カメラ」の赤外線感度を調べてみました。「同じ基準」で横並びに比べ、赤外線が写る・写らないを評価してみたのが下の○×表です。(参考:iPhoneに搭載されたカメラモジュール一覧)
 下表の○×△レベルは、こんな具合でつけています。ちなみに、△(×)も×(△)も、どちらも「(周囲光がほとんどないような状態で無い限り)ほとんど見えない」と言って良いレベルです。また、◎と○も、(個体差もありますし)ほとんど差が無いレベルです。
下表の○×△レベルは、こんな具合でつけています。ちなみに、△(×)も×(△)も、どちらも「(周囲光がほとんどないような状態で無い限り)ほとんど見えない」と言って良いレベルです。また、◎と○も、(個体差もありますし)ほとんど差が無いレベルです。
- ◎:眩しいくらいにハッキリ写る(右上写真レベル)
- ○:ハッキリ写る
- △:かすかに写る(右写真レベル)
- △(×):かすか…よりさらに暗く写る
- ×(△):ほんのわずか・ほんのかすかに写る
可視光、つまり自分の目で見ることができる世界とは別の世界を眺めてみるのも面白いものです。そんな世界を眺めようとする時には、こんな表も参考になるのかもしれません。
| 機種 | メイン(背面)カメラ | フロント(Face)カメラ |
| iPhone 5 | ||
| iPhone 4s | ||
| iPhone 4 | ||
| iPhone 3GS | ||
| iPad mini | ||
| iPad 2 |
2013-02-04[n年前へ]
■ほこ×たて!超高輝度ライト v.s. 絶対透けないスクラッチ! 
 アタリやハズレといった情報が銀色のコーティングで覆われていて、そのコーティングをコインなどではがすことでアタリかハズレか?がわかる「スクラッチカード」は、後ろから強い光を当てることで、コーティングの下に隠されている文字が読み取られてしまうことも多いものです。
アタリやハズレといった情報が銀色のコーティングで覆われていて、そのコーティングをコインなどではがすことでアタリかハズレか?がわかる「スクラッチカード」は、後ろから強い光を当てることで、コーティングの下に隠されている文字が読み取られてしまうことも多いものです。
 「高輝度ライトでも透けません!」と謳った「HI セキュリティ 銀スクラッチカード」を見かけました(右下写真)。…もしも、凄まじく明るい超高輝度ライトで、この絶対透けない銀スクラッチカードを後ろから照らしたらどうなるのだろう?と思います。
「高輝度ライトでも透けません!」と謳った「HI セキュリティ 銀スクラッチカード」を見かけました(右下写真)。…もしも、凄まじく明るい超高輝度ライトで、この絶対透けない銀スクラッチカードを後ろから照らしたらどうなるのだろう?と思います。
「どんな盾も突き通す矛」と「どんな矛も防ぐ盾」がもしも戦ったなら一体どっちが勝つか?にワクワクさせられるように、超々高輝度ライトと超高度セキュリティな銀スクラッチカードが互いに戦ったとしたら、アタリとハズレは果たして透けて見えるか・見えないのか…戦いの結果は一体どうなるのでしょうか?
 …というわけで、超々高輝度ライトと超高度セキュリティな銀スクラッチカードを軽くスパーリングさせてみた結果、今日の練習試合・プレマッチの限りは、「超高度セキュリティな銀スクラッチカード」に軍配が上がりました。銀スクラッチの下に隠されたQRコード、そのパターンを読み取ることは(高輝度ライトで背面から照らしてみても)読み取ることはできませんでした。
…というわけで、超々高輝度ライトと超高度セキュリティな銀スクラッチカードを軽くスパーリングさせてみた結果、今日の練習試合・プレマッチの限りは、「超高度セキュリティな銀スクラッチカード」に軍配が上がりました。銀スクラッチの下に隠されたQRコード、そのパターンを読み取ることは(高輝度ライトで背面から照らしてみても)読み取ることはできませんでした。
2013-02-05[n年前へ]
■「中国語版ブランド名」10個全部読めるかどうか挑戦だ!? 
 「中国語版ブランド名」10個全部読めるかどうか挑戦だ!?を書きました。
「中国語版ブランド名」10個全部読めるかどうか挑戦だ!?を書きました。
家楽氏とか喜力といった漢字の並びは、何だかとても新鮮に見えたりします。中国語(外国語)の読みを考えるパズル、結構面白いと思いませんか?
2013-02-09[n年前へ]
■「エアロ」が売りな自転車は"空気抵抗(圧力)分布例"をカタログに載せて欲しい!? 
「軽~い自転車が欲しい」と思ったりする時、「おいおい、自分の体重(脂肪)を減らす方が効率いいだろ?」という声が聞こえます。そしてまた、「一切ムダの無いエアロ形状」なんて謳った宣伝文句に目を奪われた時には、「自転車はエアロでも、そこにまたがってる”ボディ”がエアロじゃないから!」というツッコミが聞こえてきます。

数値計算フレームワークのOpenFOAMのチュートリアル、走るオートバイの空気抵抗を求めるサンプルを動かし、バイクの各部分が受けてる空気抵抗(圧力)を眺めてみると、空気にぶつかっていく先端部分に(空気抵抗は)ほぼ集中しているよなぁ…と感じさせられます。たとえば、上の画像はバイクや乗員が受ける圧力を色で示し、さらに空気が流れる流線を重ねたものですが、空気を切り裂く先端部分に圧力がほぼ集中していることがわかります。
 「エアロ形状」を売りにする自転車などは、こんな"空気抵抗(圧力)分布例"をカタログに載せるといいのではないかと思います。そんなデータを眺めれば、自転車・乗員含めた上での「この風に・こんな程度(量)、空気抵抗が低減できているんですよ(こんな体型・姿勢の人ならね)」といったメリットがわかりやすくなるような気がします。あるいは、メリットがあまりなさそうであれば、買ってから後悔することも少なくなるように思います。
「エアロ形状」を売りにする自転車などは、こんな"空気抵抗(圧力)分布例"をカタログに載せるといいのではないかと思います。そんなデータを眺めれば、自転車・乗員含めた上での「この風に・こんな程度(量)、空気抵抗が低減できているんですよ(こんな体型・姿勢の人ならね)」といったメリットがわかりやすくなるような気がします。あるいは、メリットがあまりなさそうであれば、買ってから後悔することも少なくなるように思います。
2013-02-11[n年前へ]
■「風速60kmの疑似おっぱい」を感じる大仏の掌を真面目に計算してみよう!? 
 十数年前、「風速60kmは疑似おっぱいの感触か?」という大問題を追いかけました(参考:オッパイ星人の力学 仏の手にも煩悩編、擬似オッパイに関するhiraxの関係式)。そして、疑似おっぱいの感触を説明するために必要な科学について学びました(たとえば、ナヴィエ・ストークス方程式は疑似オッパイのパラドックスを解決するために登場したといった歴史的経緯など)。
十数年前、「風速60kmは疑似おっぱいの感触か?」という大問題を追いかけました(参考:オッパイ星人の力学 仏の手にも煩悩編、擬似オッパイに関するhiraxの関係式)。そして、疑似おっぱいの感触を説明するために必要な科学について学びました(たとえば、ナヴィエ・ストークス方程式は疑似オッパイのパラドックスを解決するために登場したといった歴史的経緯など)。
その時は、疑似おっぱいの感触を感じる掌周りの空気流を計算するために、「指周囲」の流体計算をしました。しかし、それでは不十分極まりない!と反省し、今日は「風速60kmの風に疑似おっぱいを感じ取る掌」周りの空気流を3次元で計算してみました。計算対象の掌は、(十数年前の前回と同じように)ビッグな東大寺の大仏さまの掌サイズです。

計算のようすが、たとえば上の画像です。掌の周り(特に後方)で空気がうずまき、掌の前の部分では空気圧が高まり、掌の後方では空気圧が低くなっています。
計算結果を簡単にまとめると、”風を受ける掌の前後で50パスカルの圧力差が発生し、その圧力差が大仏の掌に与える力はおよそ50ニュートン…つまり風速60km/hの風は大仏の掌に5kgの重さを感じさせる”という具合です。
 (大仏の掌)一個あたり5kgの疑似おっぱい…。私の知る限りでは、Gカップが一個あたり1kgナリです(松坂季実子
(大仏の掌)一個あたり5kgの疑似おっぱい…。私の知る限りでは、Gカップが一個あたり1kgナリです(松坂季実子主演のビデオ内で行われた実験にもとづく)。ということは、大仏の掌に風速60km/hの風をあてると、大仏はGカップ5個分の疑似おっぱいを感じていることになります。
風速60km/hは東大寺の大仏なら、Gカップ5個分の疑似おっぱい、これが今日の「得する豆知識」です。
2013-02-12[n年前へ]
■天下一品とラーメン二郎を判別するための「画像処理アルゴリズム」を作ってみよう!? 
 東京が誇る「ラーメン二郎」と京都が誇る「天下一品(ラーメン)」を区別する画像処理アルゴリズムを、今日は作ってみました。
東京が誇る「ラーメン二郎」と京都が誇る「天下一品(ラーメン)」を区別する画像処理アルゴリズムを、今日は作ってみました。
見た目(色)だけで言えば、ラーメン二郎と天下一品のスープはかなり似ています。しかし、Googleで「天下一品 こってり」と「ラーメン二郎」でイメージ検索をかけた結果(左下:”天下一品 こってり”のイメージ検索で得られた画像群、右下:”ラーメン二郎”のイメージ検索で得られた画像群)を色解析してみると、実は「区別するための手がかり」があります。
下図は、(それぞれの)イメージ検索結果の画素値群をLAB色空間にマッピングしてみた(そしてab平面で画素値群を眺めてみた)結果です。
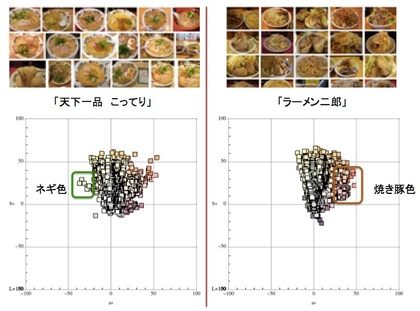
ラーメン二郎と天下一品を区別するための画像処理的手掛かり…それは「天下一品 こってり」には緑色のネギの色が入っていて、「ラーメン二郎」には焼き豚チャーシューが発する赤茶色の比率が多い、ということです。ラーメン二郎で撮影されたラーメン画像には赤茶色はあるけれど・緑色はなくて、天下一品ラーメンには緑色のネギは入っているけれど、赤茶色はそれほど入ってないのです。
ドンブリ写真から「どのラーメン店か(ラーメン二郎と天下一品)を見分けるための方法」を、今日は考えてみました。ラーメンの味を区別する、たとえば「味が薄いラーメン」「味が濃いラーメン」を区別し、好みの味かどうかをケータイ(スマホ)写真から区別することができる画像処理、そんなものを作ってみたい今日この頃です。
2013-02-13[n年前へ]
■100円で「ツナ缶開け専用器具」を作ってみよう!? 
 「ツナ缶が開けづらくて困る」ことが多い…というわけで、今日は100円で「ツナ缶開け専用器具」を作ってみました。
「ツナ缶が開けづらくて困る」ことが多い…というわけで、今日は100円で「ツナ缶開け専用器具」を作ってみました。
ツナ缶が開けづらい原因を考えてみると、
- 缶開けるのに指・爪では辛い
- 油がなかなか切れない
- 缶の隅にツナが引っかかり・取れない(スプーンやフォークでは形状が合わない) )
 そこで、この3つの課題に対して、1・3番目の課題に対しては「専用器具を作る」、2番目の課題に対しては「油の粘性を変える」、という作戦を思いつきました。つまり、こんな作戦です。
そこで、この3つの課題に対して、1・3番目の課題に対しては「専用器具を作る」、2番目の課題に対しては「油の粘性を変える」、という作戦を思いつきました。つまり、こんな作戦です。
- 100円ショップ(ダイソー)でシリコーン素材のヘラを買う
- 先を(缶サイズに合わせて)直角にカットし、ツナ缶開け専用器具を作る
- (できれば、ツナ缶を給湯器のお湯に浸け、粘性を下げておく。ちなみに、缶を熱湯に浸けると、常温時に対して粘性は1/3程度に下がります)
- ツナ缶開け専用器具で缶を少し開ける
- (ツナ缶を傾け、余分な油を出す。油は温めたことによりサラサラになっているので、すぐに出る)
- 専用器具を使うと、綺麗にすくえる!

2013-02-15[n年前へ]
■隕石・流れ星は斜め45°に降る確率が一番高い!? 
 「隕石・流れ星は斜め45°に降る確率が一番高い!?」を書きました。(関連記事:あなたと見たい、流星群 ~ 同じ流星が見える距離)
「隕石・流れ星は斜め45°に降る確率が一番高い!?」を書きました。(関連記事:あなたと見たい、流星群 ~ 同じ流星が見える距離)
すると、たとえば大気の厚みを100kmとすれば、地球への鉛直距離100kmを落ちる間に、大気に対して斜め45°に侵入してきた隕石は約100km強ほど横方向にも飛んでいきます(すごく単純に言えば、単なる2等辺3角形ですからね)。 こんな計算をしてみると、流れ星や隕石が「斜めに大きく横切っていく」というイメージは現実を反映していそうだ、と気づかされます。
2013-02-16[n年前へ]
■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ 
 数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
「ゾウさん曲線」あるいは
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?
数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
「ゾウさん曲線」あるいは
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?

実は、こういった「画像を表現するパラメータ曲線(群)」は、(かなりの部分を)自動的な作業により、比較的簡単に作り出すことができます。
それはこのような手順です。

- (通常画像から自動生成する場合)画像を白黒濃淡(グレー)画像にして、(少し画像をぼかした上で)濃淡値の等高線を作る
- (通常画像から自動生成する場合)各等高線は(画像境界部などの例外を除けば)閉曲線になっているので(等高線が途切れたりすることはないですから)、各閉曲線をフーリエ記述子で表現する
- (イラストから生成する場合)複数曲線からなるイラストを作り、各曲線をフーリエ記述子で表現する
- 各曲線を表現するフーリエ記述子の低次の項(低次の3角関数)だけ抜き出し、リストにする(並べる)
- …それらのパラメータ曲線群を並べたもの=任意の図形を描き出す曲線の集合になる
 「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
そして、そんな(単純のために閉曲線であるとします)閉曲線を描き出す(1周するごとに周期関数となる)パラメータの動きをフーリエ変換することができますから、結局のところ3角関数を重ね合わせたものをパラメータにして表現される曲線として、任意の(閉)曲線を表すことができる…というわけです。これが図形のフーリエ記述子による表現です。
 さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
これがWolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピです。…作り方を眺めてみれば、あまり「意味や価値・美しさのない曲線(存在)」に思えてしまうかもしれませんね。
2013-02-17[n年前へ]
■総額105円ナリの買い物が一番多かった2012年 
去年2012年分について、レシートを元にして「買い物時にレジで支払った金額」の頻度分布を描いてみました。横軸が「円(レジで支払った総額)」で縦軸が頻度(比率)です。
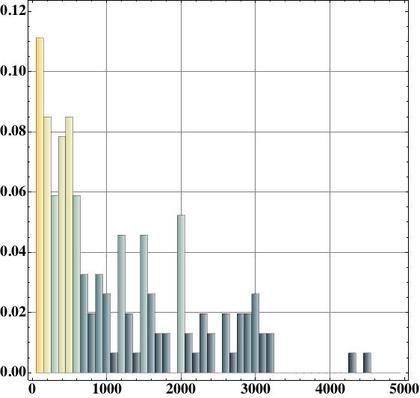
レジ支払額の頻度分布を作ってみると、意外に綺麗な分布になっています。…しかし、綺麗なのは良いとして、何だか悲しい分布です。何しろ、2012年は(レジ支払い時)総額105円ナリの買い物が一番多かったのです。つまり、「100円ショップで1品だけを買う」のが一番多かった、という状態です…。
「お金持ち層の支払金額頻度分布」は、こんな分布にはならないに違いありません。第一、レジで1000円以下のものを買うことなんて、(お金持ち層は)きっとないような気がします(想像ですけど)。
2013-02-18[n年前へ]
■おっぱい解析向けライブラリを書いてみる!? 第2回 
 おっぱい解析向けライブラリを書いてみる!? 第1回の続編です。
おっぱい解析向けライブラリを書いてみる!? 第1回の続編です。
「おっぱい解析」をしようとした時、ゼロからコードを書かなくてはならないというのは、非常に不便極まりない話です。「車輪の再発明をするな」というアドバイスが、おっぱい解析の世界ではないがしろにされているようにも思われます。…そこで、地球上のおっぱい解析研究者のために、おっぱい解析向けライブラリを書いてみることにしました。
今日書いたのは、アンダーバスト(cm)とカップサイズ(A,B,C…)からバスト(ブラジャー)のワイヤー直径を求める関数 cupDiameterFromUnderbustAndCupと、バスト(ブラジャー)のワイヤー直径からバストの体積(一個あたり)を求める関数 cupVolumeFromCupDiameterです。
cupDiameterFromUnderbustAndCup[
under_,(*cm*)
cup_ (* char *)
] := Module[
{cupInt = ToCharacterCode[cup][[1]] - 64,
initSize = 8.3,(*8.3 or 9.7*)
diffCup = 0.98(*0.98 or 0.847*)},
initSize + diffCup*((under - 65)/5 - 1)
+ diffCup*(cupInt - 1)
] (* cm *)
cupVolumeFromCupDiameter[ diameter_(*cm*) ] := 2/3 Pi (diameter/2)^3 (* cm^3 *)
これらの関数を使うと、たとえば、アンダー75(cm)のCカップのブラ(ワイヤ−)直径は、こんな風に計算できます。
cupDiameterFromUnderbustAndCup[75, "C"] →11.24(cm)あるいは、
cupVolumeFromCupDiameter[ cupDiameterFromUnderbustAndCup[75, "C"] ]とすれば、アンダー75のCカップのブラ体積(cm^3)を知ることができます。ちなみに、答は371立方cmになります。つまり、(脂肪をほぼ水と同じような密度と近似すれ阿)350mlのペットボトルとほぼ同じ重さ、ということになります。
ついでに、アンダー75cmのA~Iカップの(1個あたり)体積を計算して、チャートとして描いてみると、下のグラフのようになります。横軸の1~9は、A~Iカップを表しています。
ListPlot @
(cupVolumeFromCupDiameter @
(cupDiameterFromUnderbustAndCup[75, #]) & /@
{"A", "B", "C", "D", "E", "F", "G", "H", "I"})
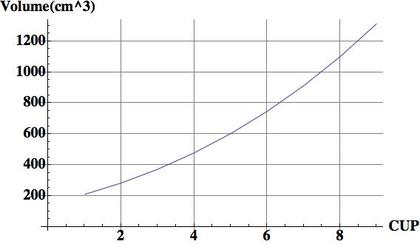
役に立つような、まったく何の役にも立たないような、そんなおっぱい解析向けライブラリを今日は書いてみました。ちなみに、このブラサイズからの算出関数が出す値は Title: Breast volume and bra sizeというInternational Journal of Clothing Science and Technology(2011)中の実測データとも、おおよそ合うようです。
C#版:C# でおっぱい解析向けライブラリを書いてみる!! 第2回
2013-02-19[n年前へ]
■ブラの”カップサイズ”が変わっても"おっぱい径"は(あまり)変わらない!という驚愕の真実 
 JIS規格JISL4006 「ファンデーションのサイズ」はブラジャーのカップサイズを「アンダーバストとトップバストの差」で定義しています。たとえば、アンダーバストとトップバストの差が10cmならAカップ、12.5cmならBカップ…という具合です。
JIS規格JISL4006 「ファンデーションのサイズ」はブラジャーのカップサイズを「アンダーバストとトップバストの差」で定義しています。たとえば、アンダーバストとトップバストの差が10cmならAカップ、12.5cmならBカップ…という具合です。
実は、カップサイズ(つまりアンダーバストとトップバストの差)が変化しても、ブラジャーのカップ径(つまりオッパイの径)の大きさはさほど変わりません。たとえば、アンダー75cmの場合、カップサイズがAカップからGカップに、つまりアンダーバストとトップバストの差が10cmから25cmに2.5倍になったとしても、カップ径は10cmから15cmへと1.5倍変化するだけに過ぎません。(参考:おっぱい解析向けライブラリを書いてみる!? 第2回)
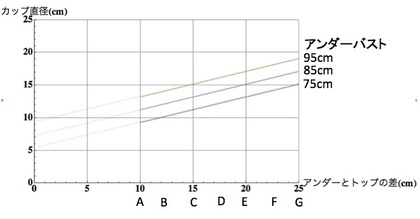
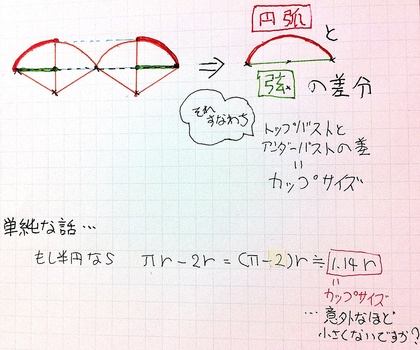
これは、とても重要な事実です。なぜかというと、もし カップサイズがブラジャーのカップ径と比例していたならば、カップサイズがAからGにアンダーとトップの差で2.5倍になるとブラのカップ径も2.5倍になり、ブラジャーの体積は2.5の3乗で約17倍にもなってしまいます。…17倍大きいおっぱいなんて、それはちょっとありえません。
 しかし、ブラの”カップサイズ”が変わっても"おっぱいの半径"は(あまり)変わらず1.5倍にしかならないとするならば、AカップとGカップのおっぱい体積は1.5の3乗でほんの3倍しか違わないことになります。つまり、AカップもGカップもおおよそ同じオーダーなのです。…この数字なら、自然に納得できる値です。
しかし、ブラの”カップサイズ”が変わっても"おっぱいの半径"は(あまり)変わらず1.5倍にしかならないとするならば、AカップとGカップのおっぱい体積は1.5の3乗でほんの3倍しか違わないことになります。つまり、AカップもGカップもおおよそ同じオーダーなのです。…この数字なら、自然に納得できる値です。
 以前、どこぞのアホが「「Cカップのバストなんて実在するわけがない!」ことの数学的証明」なんて記事を書いていましたが、それはバスト径がアンダーバストに(切片無しに)比例するというモデルを使ったがゆえの間違いです。
以前、どこぞのアホが「「Cカップのバストなんて実在するわけがない!」ことの数学的証明」なんて記事を書いていましたが、それはバスト径がアンダーバストに(切片無しに)比例するというモデルを使ったがゆえの間違いです。
現実にはCカップは存在するし、Gカップも存在します(たぶん)。…それは、ブラの”カップサイズ”が変わっても"おっぱい径"は(あまり)変わらない!という驚愕の事実がゆえなのです。
2013-02-21[n年前へ]
■「コンテキスト(背景)から独立して写真を見ることはできない」ことを「キャパの反転写真」で確認してみよう!? 
 横浜美術館で「ロバート・キャ パ/ゲルダ・タロー 二人の写真家」が開催されています。
横浜美術館で「ロバート・キャ パ/ゲルダ・タロー 二人の写真家」が開催されています。
ロバート・キャパ(Robert Capa)とは、写真家のフリードマン・エンドレ・エルネーとゲルタ・ポホイルによって作り出された架空の人物。(彼らは)写真を売り込むために「ロバート・キャパ」という架空のアメリカ人写真家を創作した。架空のキャパ名義を使うと3倍の値で売れたとされている。
下の写真は、「ロバート・キャ パ/ゲルダ・タロー 二人の写真家」のリーフレットです。眺める視線を打ち抜くように銃を構える女性兵士、眺める視線に打たれたかのように倒れる兵士…けれど、このリーフレット、実はどこかが「違って」います。

だから、私たちは撃たれる兵士の側(左)から写真を眺め、撃たれたかのように見える兵士と同じように(右側から飛んでくるかに見える弾丸の衝撃を)体に感じる、というのが、この写真の(本来の)コンテキスト・文脈なのです。

こんな風に「反転写真(と元の写真の違い)」を眺めると、私たちが「コンテキスト(背景)から独立して写真を見ることはできない」ということに気づきます。
さて、(写真が)左右対称な下の2枚チラシは、どちらが「本来」のものでしょう?…左の「(私たちの視線に相対するように)私たちに向かいレンズを構えるカメラマン」が正しいのか、それとも、私たちの視線が動く先(視線の先)にカメラがあり、何かをフィルムに写しているのか」…正しいのは一体どちらでしょうか?


答はもちろん、左側です。この(左側から読む)横書きのチラシ中では、写真中のカメラマンたちは左側を向くしかありえません。右側にレンズを向けたとたん、鋭くレンズで被写体を狙う(私たちの視線を打ち抜く)カメラマンではなくなり、私たちと同じようなただの人…になってしまいます。
私たちは、コンテキスト(背景)から独立して写真を見ることはできないのです。
2013-02-22[n年前へ]
■証明写真とプリントシールで「美人の秘密」を科学する 
 アスキーPC 4月号が届きました。掲載されている記事は、題して、『証明写真とプリントシールで「美人の秘密」を科学する』です。
アスキーPC 4月号が届きました。掲載されている記事は、題して、『証明写真とプリントシールで「美人の秘密」を科学する』です。
作り上げた「張りぼてモデルさん」を入れたリュックを背負い、買い物客でにぎわうショッピングセンターに行き、プリントシール器と証明写真機の比較撮影実験を行ってみました。…組み立てた三脚の上にモデルさんの頭部を取り付けた途端、さらに視線が周囲から集まってきます……。
 マネキンヘッドや「実物大の顔(ハリボテ)」をリュックサックに背負い、賑わうショッピングセンターに行くのは、結構度胸が入ります。リュックから(記事中では使いませんでしたがマネキンヘッドや)ハリボテ顔を取り出すと、自分がまるで旧約聖書に登場するモーゼになったかのように、海ならぬ自分の周りがすぅーっと引いていくのを感じるのです…。
マネキンヘッドや「実物大の顔(ハリボテ)」をリュックサックに背負い、賑わうショッピングセンターに行くのは、結構度胸が入ります。リュックから(記事中では使いませんでしたがマネキンヘッドや)ハリボテ顔を取り出すと、自分がまるで旧約聖書に登場するモーゼになったかのように、海ならぬ自分の周りがすぅーっと引いていくのを感じるのです…。

2013-02-23[n年前へ]
■「国会議事堂の向き」のヒミツ!? 
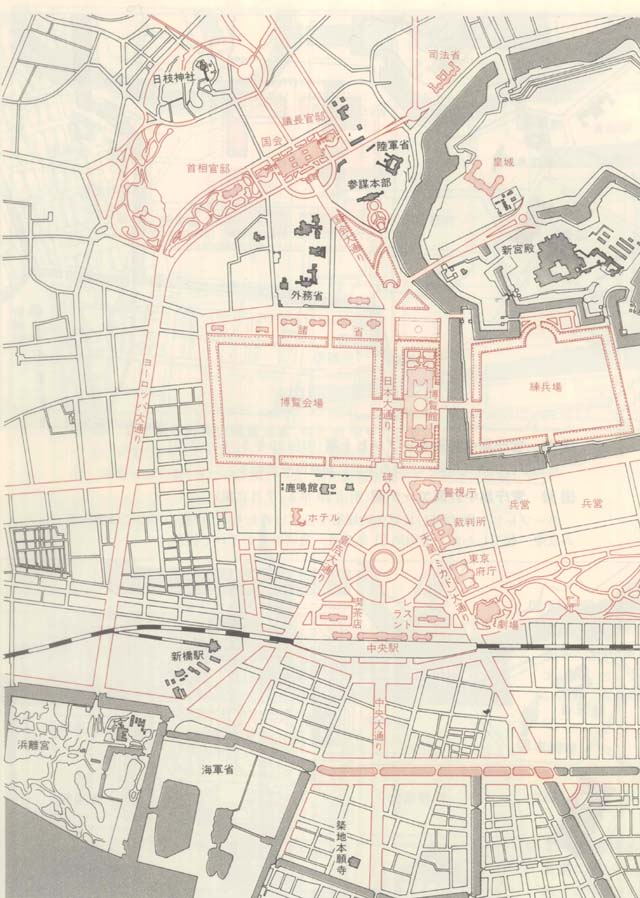 「国会議事堂の向き」のヒミツ!?を書きました。
「国会議事堂の向き」のヒミツ!?を書きました。
国会議事堂を地図上でよくよく眺めてみると、南北東西の方角から少しズレていることがわかります。国会議事堂の入り口は真東ではなく少し北寄りを向いていますし、参議院も北側というより北北西に位置しています。…ということは、玉座は完全には南面(南を向く)していないということになります。一体なぜなのでしょう?
2013-02-24[n年前へ]
■「ケーニヒスベルクの橋渡り問題」鶴見川サイクリングロード(新横浜) 編 
 街で見かけた「ケーニヒスベルクの橋渡り問題」を集めています。
街で見かけた「ケーニヒスベルクの橋渡り問題」を集めています。
「街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、(どこでも良いから)スタート地点に戻ってくることができるか?」というのは、オイラーが解いた「ケーニヒスベルクの橋渡りの問題」です。…この「ケーニヒスベルクの橋渡りの問題」は、私たちの住む街にも、実はたくさんあったりするものです。下の写真は、神奈川を流れる鶴見川の中程、新横浜近くの川縁で見かけた「ケーニヒスベルクの橋渡り問題」新横浜 編です。
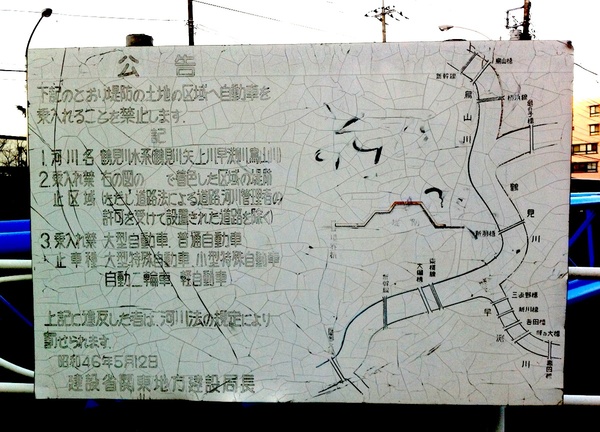
今回の問題は「一筆書き可能」のようです。…ということは、この場所を自転車やランニングでリアルに走り、「ケーニヒスベルクの橋渡り問題」を体感してみるのも面白いかもしれませんね。
2013-02-25[n年前へ]
■「僕が一番欲しかったもの」 
 昨年(2012年)の年末、大晦日イブに「デジカメでレイトレしません?」とtwitterで囁(ささや)かれました。…もちろん、そう言われたら、間髪おかずに「はい、喜んで!」と答えるに決まっています。…そういうわけで、年末の大忙しの(はずの)大晦日、デジカメ・レイトレコードを書きました(参考:デジカメ内部でレイトレーシング計算をさせてみる!?、続 デジカメ内部でレイトレーシング計算をさせてみる!?)。
昨年(2012年)の年末、大晦日イブに「デジカメでレイトレしません?」とtwitterで囁(ささや)かれました。…もちろん、そう言われたら、間髪おかずに「はい、喜んで!」と答えるに決まっています。…そういうわけで、年末の大忙しの(はずの)大晦日、デジカメ・レイトレコードを書きました(参考:デジカメ内部でレイトレーシング計算をさせてみる!?、続 デジカメ内部でレイトレーシング計算をさせてみる!?)。
 そんなコードを(「デジカメでレイトレなコードを書きましょう!」とtwitterで囁いた方が)紹介する「Extreme aobench - Syoyo Fujita (TokyoDemoFest 2013 seminar)」を観ました。
そんなコードを(「デジカメでレイトレなコードを書きましょう!」とtwitterで囁いた方が)紹介する「Extreme aobench - Syoyo Fujita (TokyoDemoFest 2013 seminar)」を観ました。
「デジカメでレイトレーシング」が紹介された瞬間、会場に広がったカラッとした空気(くだらね~頭のネジがちょっと変~と何だか鼻で笑われた感じ)の笑いが最高に嬉しい!と感じました。それこそ、これこそが一番欲しかった「報酬」だったんだ!と気づかされました。
くだらなくて・役立たずで・頭のネジがちょっと変…って、最高の反応じゃない?と思う2013年の2月の終わり、です。
2013-02-26[n年前へ]
■一瞬で消せる「フルカラープリント」を作ってみた! 
 PILOTのフリクションボールは、温度が高くなると色が消えるインクを使ったボールペンです。レーザビームプリンタ(LBP)などは、インク(トナー)を高温で溶かして紙に固着させるので、フリクションボールで文字などが書かれた紙を(高温の過程を経る)LBPに通すと、フリクションボールで書いた部分を(気持ち良いくらい)綺麗さっぱり消すことができます。そこで、最近では、そんなインク(トナー)を使ったプリンタ・コピー機が発売されていたりもします(東芝テック Loops)。
PILOTのフリクションボールは、温度が高くなると色が消えるインクを使ったボールペンです。レーザビームプリンタ(LBP)などは、インク(トナー)を高温で溶かして紙に固着させるので、フリクションボールで文字などが書かれた紙を(高温の過程を経る)LBPに通すと、フリクションボールで書いた部分を(気持ち良いくらい)綺麗さっぱり消すことができます。そこで、最近では、そんなインク(トナー)を使ったプリンタ・コピー機が発売されていたりもします(東芝テック Loops)。
 …しかし、残念なことに、まだ単色のプリントしかできません。そこで、今日は「一瞬で消せるフルカラープリント」を作ってみました。やり方はとっても簡単です。4色のフリクションボール、「黒(K)・シアン(C)・マジェンタ(M)・イエロー(Y)(っぽい色)」を買い、後はひたすらガッツな手作業でフルカラー画像を描き出してみたのです(CMYKの4色を適切に使えばフルカラー画像を描くことができるのです)。
…しかし、残念なことに、まだ単色のプリントしかできません。そこで、今日は「一瞬で消せるフルカラープリント」を作ってみました。やり方はとっても簡単です。4色のフリクションボール、「黒(K)・シアン(C)・マジェンタ(M)・イエロー(Y)(っぽい色)」を買い、後はひたすらガッツな手作業でフルカラー画像を描き出してみたのです(CMYKの4色を適切に使えばフルカラー画像を描くことができるのです)。
フルカラー画像を4本のボールペンで描いてみた後に、(レーザビームプリンタなどがインクを溶かす温度とほぼ同じ)180℃ほどに熱した(逆さにした)フライパンの上に、手書きフルカラープリント用紙を載せてみると…一瞬でカラー画像が消え・真っ白な紙へと戻っていきます。つまり、一瞬で消せる「フルカラープリント」のできあがり!です。
今日作ってみた「一瞬で消せるフルカラープリント」は、ポップ・アートの(アンディ・ウォーホルと並ぶ)代名詞画家、ロイ・リキテンスタイン(Roy Lichtenstein)の”M-MAYBE”です。消えるのは「一瞬」でしたが、4色のボールペンでフルカラー画像を手作業で描くのは、優に2時間かかってます。描くのは2時間、消すのは一瞬…今日は「一瞬で消せるフルカラープリント」を作ってみました。
フルカラープリントが一瞬で消えてしまったか…と思いきや、フリクションボールのインクは消した後「冷蔵庫に入れて冷やすと、復活する!」ということで、今は冷凍庫でロイ・リキテンスタイン(Roy Lichtenstein)の”M-MAYBEはリハビリ色復活中…です。I'll be back!