hirax.net::inside out::2013年07月

■１月・２月・３月の高出生率のヒミツ!?　

　1899年から2000年までの月別出生率を見ると、昭和20年くらいまで、１月・２月・３月の出生率が高いことに驚きます。下のグラフが、その「1899年から2000年までの月別出生率」ですが、「１月・２月・３月の出生率が他の月の1.5倍くらい高い」「一番出生率が少ない６月と比べると２倍ほど高い」という具合になっています。これは、一体なぜなのでしょうか。

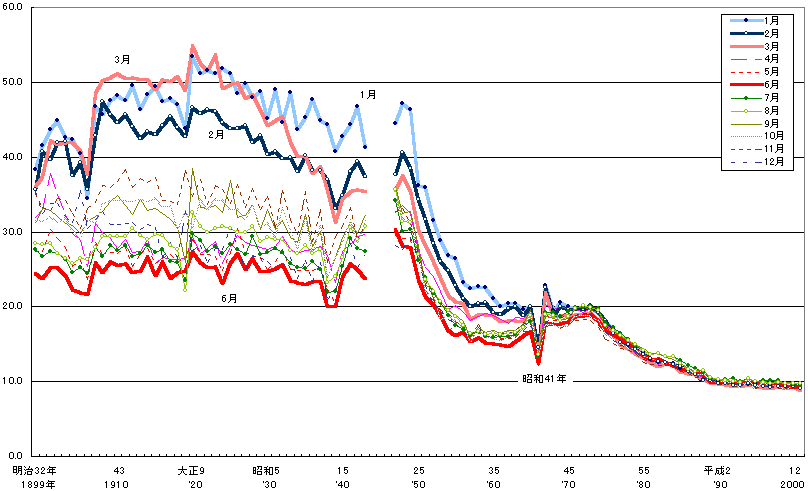
　「農作業を行う貴重な労働力を無駄にしないために、農作業オフシーズンの時期に出産をするように計画出産をした」とか「（出産の約９ヶ月前にあたる）春という季節は恋と愛の季節だ」とか…色々な理由が考えられそうですが、このデータやはり何だかとても不思議でミステリアスです。

　たとえば、１・２・３月以外の出生率は、長い間（それほど）変わっていないにも関わらず、１・２・３月に限っては、1905年あたりから急に上昇しています。都会で働く職業の人たちが増えたこの時期、そんな風に急激な変化があると、何かの制度とかシステムとか…そんな変化があったのだろうか？と想像したくもなったりします。

　…この理由は、一体どんなことなのでしょうか。その時代は、どういった変化があった時代だったのでしょうか。

■ツール・ド・フランスの選手１人で「４０畳用エアコン」を動かせる！？（…５人くらいでないと無理でした）　

　ツール・ド・フランスの選手１人で「４０畳用エアコン」を動かせる！？（…５人くらいでないと無理でした）を書きました。

　たとえば、昨年のツール・ド・フランスの優勝タイムは87時間34分47秒です。 この時間で、トータル141666 kcalの運動を選手たちがしたということは、選手たちの仕事率（時間あたりに行った仕事量）を計算すると1880 ワットに相当します（80W程度の基礎代謝分は含まない計算です）。

■iPhone 4で撮影した「可視光景色と赤外線景色のモーフィング」　

　iPhone 4のメイン（背面）カメラは赤外線を写すことが（ほぼ）できません。しかし、フロントカメラ(Facetime Camera)は、（感度は高くないですが）赤外線を写すことができます。そこで、森の中にあるゴルフ場と都会にある陸上競技場のグランドで、通常の可視光写真と赤外線写真の両方を撮影し、それらのモーフィング画像を作ってみました。

　可視光では明るく見える空が赤外線写真では暗い空になり、可視波長で見ると鈍く暗い緑の森が赤外波長では明るく眩しく輝いていたりすることがわかります。だから、たとえば可視光では木々の中に埋もれていたコンクリート部分が、赤外線で眺めると見事に浮かび上がってきたりするのです。

■「アイドル（偶像）の力」と書いて「無限大」と読む　

　「できること」を決めるのは「気持ち」と「やる気」だ。前者は「思い込みや勘違い」という言葉と区別することが多分不可能な存在で、後者は「行動を実際に起こす」ということを言い換えた言葉だ。

　（ハッカーという言葉に憧れるミーハーな奴らには）気持ちをぶつけ・行動を起こす武器であるノートPCに、（アイドル）菊池桃子さんのサインを力強く書いてもらった。AppleのMacBook Airだからといって…もちろん以前AppleのCMに出ていた（ある種伝説になった）（微妙な一字違いの）菊地桃子さんじゃない。雑誌Momocoの表紙を飾り続けた菊池桃子さんだ。

　１００倍パワーアップした道具を手に持てば、思い込みパワー的に言えば、当社比１００倍のコードを書けそうな気がするし、…あるいは「やる気パワー」的に言うならば、それだけの行動をしなければ「何だかダメ」であるような気がする。１００倍パワーアップした道具なら１００倍のことができそうな気がする。

　最高のバースデイプレゼントですね。
　　　7月10日 20:47

　この道具でコードを１００倍書いた時、そのコードこそが最高のバースデイプレゼントなんだと思います。
　　　7月10日 20:56

　「偶像」と書いて「アイドル」と読む。けれど、その偶像の力は無限大なのかもしれない。…もしも、そんなことができたなら、アイドルのファンが「できたこと」こそが、アイドルがファンに与える力であるかもしれないし…もしかしたら、ファンがアイドルに与えることができる「力」なのかもしれない。

　…というわけで、MacBook Airにサインを貰ったから、今日から１００倍コードを書こうと思う。

■「１５から３５歳のくらいの頃」には「夢を見たい」　

　「いつやるか? 今でしょ!」の林 修 先生（というか東進ハイスクール）をそのままパクった…じゃなかったインスパイアされた宣伝ビデオを１年少し前に作った。インスパイア・ビデオを作ってしばらくした頃、林先生の「いつやるか? 今でしょ!」が超華々しくブレイクしたから、今やそのビデオは、林先生の人気に丸々乗っかったインスパイアされたどころか、丸々パクったビデオにしか見えない（実際その通りだ）。

　…そのビデオ中に登場するMacBook Airには、今は菊池桃子さんのサインが入ってる。３０年前の雑誌「Momoco」を毎月買ってた１５歳の自分は、そんな「（他の人から見れば小さいかもしれない）幸せ」の可能性なんて、夢にも思わなかった。

　林 修 先生は４７歳だけど、３０年前の１７歳の頃、あるいは２０年前の２７歳の頃、今の林 先生の姿を想像していたのだろうか。

　「可能性」なんて多分勝手に狭まっていくものだから、だからこそ、その可能性を自分で狭めるのは「つまんない」と思う。夢なんて、多分叶わないものだけど、だからこそ、夢を見ない人生はつまらないと思う。わざわざ、可能性を削ることをセルフサービスでしてしまうのは…何だか違う。

　少なくとも、１５歳から３５歳のくらいの頃、「夢を見ない」のはもったいないと思う。

■「風でめくれるスカート」の科学！「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則　

　「風でめくれるスカート」の科学！「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則を書きました。

　計算してみると色んなことがわかる！というわけで、今回は「風でめくれるスカート」を科学してみました。「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?くらいの力が生じてしまうのです。

　スカートが風でめくれ上がってしまう…というと、「強風の時、スカートの前後どちらを押さえますか？」という小町さんたちの議論も面白い。

8:26 AM

■「10%ゼラチン・ゼリーの柔らかさ」は「おっぱいより、ほんの少し堅いくらい」という必ず役に立つ豆知識!?　

　食品学の本に、10%ゼラチンゼリーのヤング率は240,000 (dyn/cm^2）だと書いてありました。240,000 (dyn/cm^2）ということは、SI単位に変換すると2.4×10^4 Pa です。ヤング率は、「変形させるために必要な応力」ですから、ヤング率が小さい方が柔らかく（＝軽い力で大きな変形を生じさせることができる）・大きい方が堅く（変形させるのに大きな力が必要）なります。ちなみに、ダイヤモンドのヤング率は1×10^12 Pa ほどです。

　さて、乳房の脂肪組織の剛性率は 0.5〜25×10^3 Paで、乳腺組織はその数倍程度ですから、それらを合わせて考えてみると、乳房＝おっぱいのヤング率は、2×10^4 Paくらいであると（超大雑把に）見積もることができます。

　つまり、10%ゼラチン・ゼリーのヤング率はおっぱいのヤング率とほとんど同じくらいなのです。あるいは、それを言い換えれば、「10%ゼラチンゼリーの柔らかさ」は「おっぱいより、ほんの少し堅いくらいの柔らかさ」ということになります。

　10%ゼラチンゼリーの柔らかさ・堅さがわからなかったら、その時はおっぱいの柔らかさ基準で考えてみれば良いのです。ゼラチンが少なめだからおっぱいと同じ柔らかさかな？とか、ゼラチン多めだから少し堅いおっぱいかな？と考えれば良いのです。「10%ゼラチン・ゼリーの柔らかさ」は「おっぱいより、ほんの少し堅いくらい」…これは、とても役に立ちそうな豆知識ですよね！

関連する面白い読み物：かたいプリンが大好きだ！

■「時速60kmの風」は「アンダー85cm Cカップを1.3mm押し込む感触」で「ウィダーゼリーの重さ」とほぼ同じ!?という法則　

　「風でめくれるスカート」の科学！「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則で使った、風速から圧力（あるいは力）の計算式を使うと、興味あるさまざまな数値を導き出すことができます。たとえば、時速60kmつまり秒速16.7m/sの風を受けるときの圧力はおよそ170 Pa 程度になる、ということがわかります。

　「時速60kmの風に掌を差し出すと、Cカップのおっぱいの感触を感じる」と言いますが、時速６０ｋｍの風に向けた掌が感じる感触（圧力）を定量的に言うならば、それは170 Pa 程度という数値です。

　さらに、「10%ゼラチン・ゼリーの柔らかさ」は「おっぱいより、ほんの少し堅いくらい」という必ず役に立つ豆知識!?で書いたおっぱいのヤング率（1×10^4 Pa程度）を使うと、もっと細かで具体的なことも計算することだってできます。それは、たとえば「掌が170 Paを感じる時、（それは）何カップのおっぱいを、どんな触り方をした時の感触と同じか？」ということだってわかります。

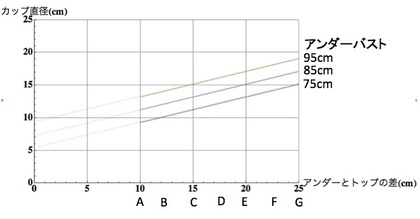　ヤング率が1×10^4 Pa程度であるおっぱいに、170 Pa　の圧力をかけると、厚みが２％ほど縮みます。アンダーバスト85cmのCカップの場合、オッパイの最厚長は約65mmなので、これはつまりアンダー85cmCカップのおっぱいを1.3mmほど押し縮めた時の感触と同じということになります（参考：ブラの”カップサイズ”が変わっても"おっぱい径"は（あまり）変わらない！という驚愕の真実　）

　ちなみに、掌の大きさが10cm四方…つまり0.01m^2だとすると、170 Paの圧力を受ける掌は1.7 N = 0.170kg重の力を受けます。つまり、時速６０kmの風を掌に受ける時、あるいは、アンダー85cmCカップのおっぱいを1.3mmほど押し縮める時、掌はウィダーゼリー（１パック１８０ｇです）を載せた時と同じ程度の力を受けるのです。…それを逆に言うならば、「ウィダーゼリーの重さ」がわからなかったら、アンダー85cmCカップのおっぱいを1.3mmほど押し縮める時の感触を思い出せば良い、というわけです。

　「時速60kmの風」は「アンダー85cm Cカップを1.3mm押し込む感触」で「ウィダーゼリーの重さ」とほぼ同じ!?という法則…「実に面白い！」と（少しエッチな）ガリレオ湯川先生なら叫びそうな、面白い法則ですよね。

■「下向きにかがんだ時のおっぱい変形具合」を暗算計算する方法!?　

　おっぱいのヤング率が 0.5〜25×10^3 Pa 程度という数字を使うと、たとえば「下向きにかがんだ時のおっぱい変形具合」も大雑把に見積もることができます。（参考：「10%ゼラチン・ゼリーの柔らかさ」は「おっぱいより、ほんの少し堅いくらい」という必ず役に立つ豆知識!?）

　まずは、おっぱいの形状を１０ｃｍ四方の立方体として考えてみることにします。脂肪の密度は水より少し軽い程度ですから、このおっぱい立方体の重量は約1kgです。1kg重＝9.8Nの力が１０ｃｍ四方のおっぱいに働くということは、1m^2あたりの応力に直すと、これまた大雑把に見積もるならば、おっぱいを「伸ばす」向きに9.8 N / (0.1 m × 0.1 m) ≒ 1×10^3 Paの力が掛かるということになります。

　たとえば、おっぱいのヤング率を 1×10^3 Paとすると、

おっぱいの変形（歪み量）= 1×10^3 Pa/1×10^3 Pa =1

　ここで「実に面白い点」は、「地球上で（おっぱいに）働く重力がおっぱいのヤング率とほぼ同じ」という不思議な偶然です。言い換えれば、極めて興味深い点は、地球で生活するおっぱいの変形が数倍程度に収まるような特性になっている…という奇妙な事実です。

　…しかし、考えてみればその半分は必然です。なぜなら、おっぱいのヤング率が重力に対して小さかったら、誰しも「おっぱいが地面にまで垂れる垂乳根の母状態」になってしまい、ズリズリ…とおっぱいを引きずり歩くような生物が生存することはとても難しそうだからです。

　それでは、ヤング率が高い場合＝おっぱいが堅く変形しない場合にはどうか、なぜ堅いオッパイではなかったのか…ということについては、識者のご意見を拝聴したいところです。

■「誕生日が1〜3月に集中していた戦前日本」では「誕生日のパラドックス」はどうなるか？　

　「誕生日が1〜3月に集中していた戦前日本」では「誕生日のパラドックス」はどうなるか？

　さて問題です。このような誕生日が１〜３月の時期に集中していた戦前の日本で「誕生日のパラドックス」を考えてみると、つまり「何人が集まれば、同じ誕生日の人（たち）がいる確率が50％を超えるか?」を考えてみると、一体どんな答が出てくるでしょうか？…真夏の夜に挑戦するのに丁度良い面白いパズルだと思いませんか？

■おっぱい解析向けライブラリを書いてみる!? 第3回 「胸チラを確認する表示関数」を書いてみよう!?　

　「おっぱい解析」をする時に、ゼロからコードを書かなければならないのは不便極まりない！というわけで、おっぱい解析向けライブラリを書いています（第１回・第２回）。今日は、アンダーバストと（AカップとかBカップといった）カップサイズから、胸の大きさとブラの形状等を計算・表示する関数を書いてみました（コードはコメントを追加した上で、後ほど適当な箇所に置きます）。

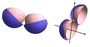
　たとえば、右上および下の図は「アンダー７０ｃｍでAカップ（トップが７０ｃｍ＋１０ｃｍ＝８０ｃｍ）の人が、70Bの3/4カップ形状のブラジャーを(重力が働く環境下で）付けた」時のようすを表示してみた結果です。

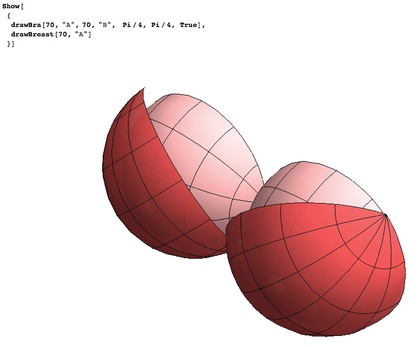
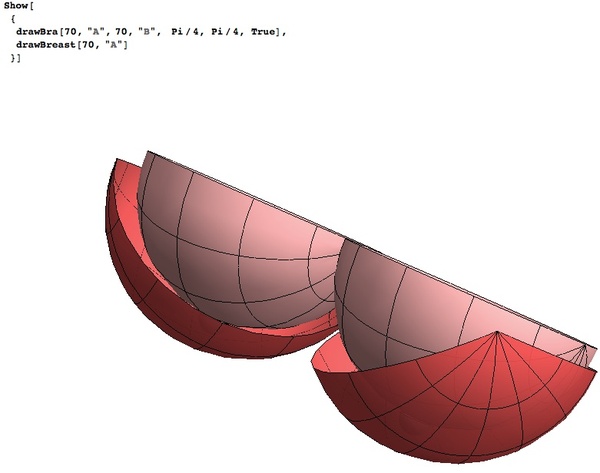
　ちなみに、こんなコードを書いてみると、あるいは、そのコードを書くために少し考えてみると、胸の先が（上から）見えてしまう可能性があるのは「アンダー65cmのB,Cカップ、アンダー70cmのA,Bカップ、アンダー75cmのAカップ程度に限られる…」という真実が見えてきたり!?します。

　この胸元が見えるかどうかは「カップサイズに依存する」「上に羅列したサイズ以外でなら（見えてしまうことを）心配しなくて大丈夫！」という理屈については、後ほど詳しく書いてみることにします。

■Thinkpad T530 ライフ（２週間）で「道具という存在」を考える　

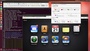
　 Thinkpad を試用することができる「ノートパソコン貸出機プログラム」で、Thinkpad T530生活を２週間ほど体験しました。システムドライブをSSDにした上で、Ubuntu 64 bitをSSDにインストールし、15.6インチディスプレイ（1920x1080）で作業をしていると、ポインティングデバイスとしてのトラックポイントと大画面環境が実に心地良く感じます。「道具」が人の可能性を拡大（あるいは縮小）する装置だったとするならば、眺めることができる世界の大きさと無関係ではない「画面の広さ」や、眺める先を効率良く指し示すためのポインティングデバイス機構は、道具の善し悪しを決める大きな材料だと思います。

　この入力デバイスは1990年にIBMの研究者テッド・セルカー（Ted Selker 正式には Edwin J. Selkar）により発案され、後にThinkPad の生産を行うことになる日本IBM大和事業所へみずから実用化をもちかけたのが起源とされる。セルカーはキーボードのホームポジションから手を離すことなくポインティングを行う装置として、このデバイスを発明した。

　車のフロントグラスは視野が広い方が良いし、車のハンドルは機敏に性格に操作できる方が良い…などということを考えるまでもなく、Thinkpad 530は心地良く使うことができる道具でした。

　Thinkpad T530 は使い勝手の良い「道具」です。強欲に（あともうひとつ）望むなら、自分の思いを具現化する道具という存在は、いつでも自分と共に連れ歩きたい…だから、その道具にはさらに薄く・軽くなって欲しいとも思います。けれど、すべてを満足する道具は（なかなか）存在し得ない以上、「こうあると良いな」と思う条件を複数備えているデバイスは、「良い道具」なのだと思います。

　ちなみに、上のスクリーンショットは SSD にUbuntuをインストールしたThinkpad 上で、Apple iCloudを使っている画面です。iCloud 上でKeynoteプレゼンテーション・ファイルを作っている…そんな作業をしている途中に撮影したスクリーンショット画面です。

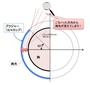
■「胸先チラリ…」の幾何学!? ー Bカップ以下の小胸さんが要注意!という証明!?　

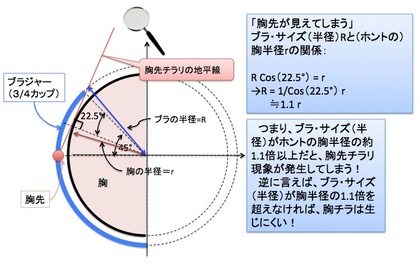　「胸先チラリ…」の幾何学!? ー Bカップ以下の小胸さんが要注意!という証明!?を書きました。

　アンダー65cmのCカップというのは、かなりレアなパターンでしょうから、実際のところ「胸先がチラリ見えてしまいやすいのは、A,Bカップにほぼ限られる」と言っても良いだろう、ということになります。

　というわけで、今回は単純な算数（数学）を使い「胸先チラリ…」の幾何学を考えてみました。数学的に導き出された結果は、胸先チラリ条件が生じるのは「ほぼBカップ以下の小胸さんに限られる！」という「なるほど、確かにそうかも！」という答えでした。

■福本伸行漫画に登場するゲームで考える「ある分野の内容を、他のことに適用してみる」ということ　

　TV番組「アメトーーク！」 の「福本伸行先生に シビれた芸人っ・・・・・・・！」を観ながら、「ある分野の内容を、他のことに適用してみる」ということについて考えました。

　福本伸行マンガに登場するオリジナル・ゲームには、他ジャンルのゲーム・ルールに基づいて作られたように見えるものがあります。

　たとえば、麻雀牌の何割かがガラス製で、牌種が全員に見えた状態でゲームが行われる 鷲巣麻雀は、手札の一部が公開された状態で行われるスタッド・ポーカー（オープン・ポーカーを麻雀に応用したものに見えますし、あるいは、カイジに登場するゲーム「救出」 は、論理パズルの典型的な題材です。つまりいずれも、ある分野の内容を、他のこと（ゲーム種や物語展開）に適用し、とても面白いものとして調理したものでしょう。

　スタッド・ポーカーはオープンなポーカーである。まず初めに各プレイヤーに何枚かの手札（枚数はポーカーの種類ごとに異なる）が裏向きに配られる。次に各プレイヤーに表向きにカードが一枚ずつ配られる。ここでまず一度ベットをする。…以下表向きのカード配布とベットとが交互に行われ、最後のベットが終わったら、全員最初に配られた裏向き札を明かし、勝敗を決める。

　完全に新しいことなんて世の中にはほとんど存在し得ないし、どんなに新しく見えることも、他の何かの影響を受けて作られるのだよなぁ…と思いつつ、「ある分野の内容を、他のことに適用してみる」ことを、２４時間３６５日、５年１０年行ったとしたら、どんなものを形作ることができるだろう…と考えます。

　世の中にあるさまざまな技術や芸術、言葉や行動といったすべてのものが、何に影響を受け・何を（他分野に）応用することで作られたかを示した系統樹を見てみたい、と思います。元あったものが、その時の状況・適用先に応じて変えられていたさまを眺めれば、そこにある「新しさ」をより強く感じられるような気がします。

■「（テキヤの）アタリのないクジ担当バイト」とか「花とゆめ」とか「誕生日」　

　最近の「いろいろ」

　「当たりの入っていないくじ引きで逮捕」という記事。…大学時代にテキ屋バイトをした。そこも１等の高額ゲーム機が当たるアタリは存在しなかった。大体、その１等ゲーム機自体、箱の中身なんかなかった。…しかし、もっと恐ろしかったのが（続く）

　１等じゃないにしても、高めの商品が当たったら、なんのかんの言って”アタリがなかったことにしてね”と、そのクジ担当のバイトには説明がされる…ということだった。テキヤバイトの中では、クジ担当は（アタリが出たら…と思うと）実につらかった。

　あと、金魚（スーパーボール）すくいも、「小さい子が１００円玉握りしめて来ると…」辛かった。水に浸った「すくい紙」が破れると…その濡れた紙の何倍のもの涙が、小っちゃな子の目に浮かぶんだもの…。

　白泉社40周年記念WEBサイトの「40作全巻622冊プレゼント」が欲しい！高校に入った'80sから「花とゆめ」を買い、大学時代は研究室の棚を「花とゆめ」で埋め尽くした。…あれ、一体いつから「花とゆめ」を読まなくなってしまったのだろう？

　誕生日の計算問題と言えば、先日飲みながら、こんな話題になった。「何人いれば、誕生日が3連チャンで繋がっている3人がいる確率が50％を超えるか？」これも、時間が空いた時にでも挑戦してみると面白い計算パズルかも。