hirax.net::inside out::2014年05月

■バンコクのカオサン近く、プラ・スメン砦の「ケーニヒスベルクの橋渡り問題」　

　街で見かけた「ケーニヒスベルクの橋渡り問題」を見かけるたびに、いつも集めています。

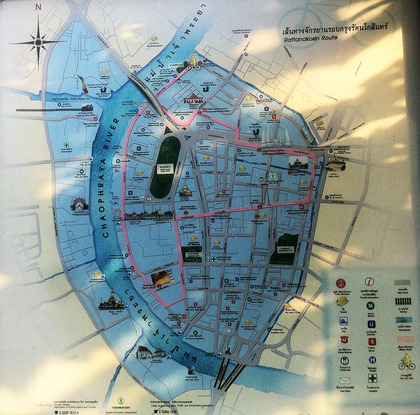
　「街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、（どこでも良いから）スタート地点に戻ってくることができるか？」というのは、オイラーが解いた「ケーニヒスベルクの橋渡りの問題」です。…この「ケーニヒスベルクの橋渡りの問題」は、私たちの住む街にも、実はたくさんあったりするものです。

■ダ・ヴィンチが描いた「モナ・リザ」の３Dマップを作ってみよう!?　

　マドリードのプラド美術館が「レオナルドと非常に近い弟子が描いた『モナ・リザ」の模写を発見した」と発表したのは２０１２年。その後、プラド美術館にある『モナ・リザ」は、ルーブル美術館にある『モナ・リザ」と同じ時に、ダ・ヴィンチが描く「モナ・リザ」を参考にしながら、近い位置から描かれたのではないか？だとすると、さながら「左右の異なる視点から描かれた立体写真のようじゃないか！」という話を読みました（Leonardo da Vinci may have invented 3-D image with ‘Mona Lisa’）。

　“This points to the possibility that the two [paintings] together might represent the first stereoscopic image in world history,” the researchers wrote in their initial report on the phenomenon last year in Perception.

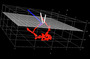
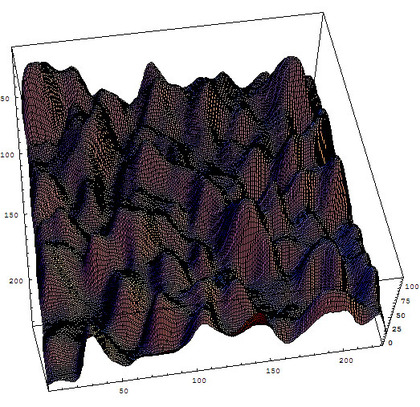　これは面白い！ということで、プラド美術館にある『モナ・リザ」とルーブル美術館にある『モナ・リザ」という「２枚の視差画像」から深度マップ（奥行きを示す画像）を作ってみたくなり、画像間の局所相関を用いて挑戦してみた結果が右の画像です。といっても、トライしてみたけれど、上手く・自然な「深度マップ」を作成することはできなかった…という具合です。

　というわけで、いつか「ダ・ヴィンチが描いたモナ・リザの３D復元画像を作るぞ！」と誓う五月初旬の土曜日です。

■オート３輪が排気ガスをまき散らしてた「あの時代」の夕焼けを眺めてみよう。　

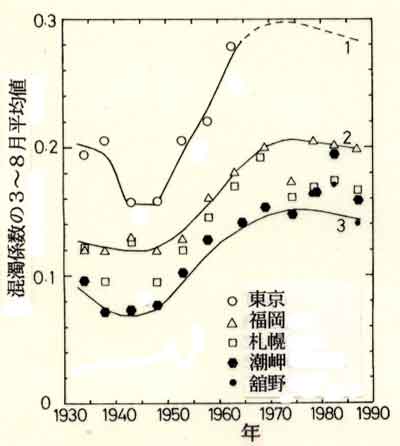　「”三丁目の夕日”の頃は大気汚染も酷くて、全然美しい時代じゃなかった*」みたいな話を読んで、ふと考えました。大気汚染が酷いならとても夕焼けが美しそうだ…。というわけで、ド派手にエアロゾル２倍の汚染状態にして、夕日レンダリングしてみました。その結果が、下に貼り付けた画像です。一番左が基準画像で、真ん中が「エアロゾル２倍な大気汚染時代」です。レイリー散乱の影響で、綺麗で赤みがかった綺麗な夕暮れ空になりました。

*三丁目の夕日の舞台となった昭和三十年代は大気混濁係数の変化を見ると、まだ大気は（現在と比べても）まだそれほど汚れてなかった時代のようです。

　そこで、さらに調子に乗り、エアロゾルを「倍々ゲーム」で倍返しだ！（古い）という感じでさらに大気汚染の度合いを増やせば、もっともっと美しいはず！と「大気汚染が進んでいるという北京の夕日」をレンダリングしてみた。それが、一番右の景色です。

　…うーん、これは少しばかり、暗く陰り過ぎな夕暮れ景色になってしまったかも。

■[今日見た景色] オート３輪が排気ガスをまき散らす街で 　

　朝、５時半に起きると、街に漂う霞みが朝焼けの赤色におぼろげに美しく染まっています。昼間にバンコクの街で自転車を漕いでると排気ガスがとても煙いけれど、朝はそれでも心地良い感じです。…というわけで、『オート３輪が排気ガスをまき散らしてた「あの時代」の夕焼けを眺めてみよう』を書いてみました。

　早朝、自転車を漕ぎながら考えました。最近、バンコクに来る時は、いつも同じアパートメントホテルに泊まり、輪行してきた自転車に乗る早朝サイクリングから始まる（いつも同じような）２４時間を過ごしています。…そのマンネリがなぜ生じているのかと考えてみると、心地良い”ある程度の最適解”に辿り着いてしまったからかもしれない…などと考えます。

　そして、ペダルを足で回しつつ考えます。「これはマズイかも、それってよくある局所最適解に陥った、鍋の中で茹でられているカエル君だよね」「もっと、色んなことにトライして苦労しないとマズイよね」

　あれ？そもそも「自分がしていたいことや目的」って一体何だったのだろう？と考えます。自分の気持ちを探ってみると、「局所最適解」に辿り着きたいわけではないような気もするし、「最適解」に辿り着くための「手段」がいつの間にか目的に成り代わってしまったかのごとく「色んなことをしてみたい」気持ちが強いような気もします。…けれど、一体それは何故なのだろう？と考えます。

　バンコクの街を朝６時に自転車のペダルを漕ぎながら、「もしかしたら…」と考えます。いつまでも続く「最適解」なんて存在しえないとか・保証できないとか、そんなことを思っていて、そんな時にも「可能性」を最大限に高めたいと思っていて、だから「色んなことをしてみたい」「色んなことができるようにしておきたい」と感じているのかも、最悪時の可能性をMaxにしたくて、「色んなことをしてみたい」気持ちが強い」のかもしれない…と思います。

■パワーポイントでスーパーマリオを楽しもう！（パワポで楽しむゲームマップ！）　

　パワーポイントを使ったプレゼンテーションで、「全体ストーリーやスライドとスライドの間の繋がりを意識しない（マズイ）症候群」を直すために*、こんなものを作ってみました。題して、パワポで楽しむゲームマップ！ Part 1 "パワーポイントでスーパーマリオを楽しもう！"です。

　ホントのところ、「全体ストーリーやスライドとスライドの間の繋がりを意識しない（マズイ）症候群」を直すため」というのは口からデマかせなウソっこです。

　パワポのスライド背景とスライド切り替え効果で、スーパーマリオブラザーズのステージ１をクリアする！気分のプレゼンテーションテンプレートです。

　今日作った「パワーポイントでスーパーマリオを楽しもう！（パワポで楽しむゲームマップ！）」なファイル（PPTX､PPT）は、ここに置いておきます。そして、昔ながらのゲームマニアから現在にまで至るまで古今東西の色んなゲームを、仕事では絶対に使うことができそうにないパワーポイント・プレゼンテンプレートを、色々作ってみようと思います。

■エクセル（に限らず）表示されてる値は「ホント」の値とイコールだとは限りません!?　

　Microsoft Excelでルックアップテーブル（入力値と出力値の対応表を使い、入力値から出力値を返す機能）を使いハマった方がいました。その状態を再現してみたのが、下に貼り付けた画面です。（画面右にある）「入力値Table(Index)と出力値Table(Value)を対応付ける対応表」を使い、LOOKUP関数およびVLOOKUP関数により、画面左上部にある入力値（Index）から値出力をさせてみたところです。見るとわかるように、入力値（Index）には1.8とタイプされていて、（対応表は入力・出力の組み合わせとして同じ値が入っているので）返ってくるのも1.8かと思いきや、出力されているのは1.7という結果です。･･･一体なぜなのでしょうか？　エクセルの「バグ」なのでしょうか？

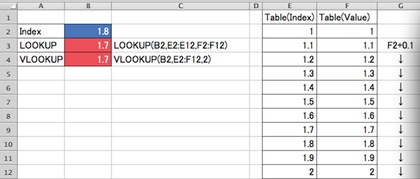
　これは、浮動小数点演算の結果によるものです。対応表は1に0.1を繰り返し足すことで作ってあるのですが、１０進法の0.1は2進法の分数で表現される浮動小数点では正確に表すことができないため、この「対応表に”1.8”と表示されている値」は、本当は1.8とイコールな値ではないのです。だから、エクセルのLOOKUP関数は1.8とイコールな箇所を見つけることができず、1.7を返すわけです。

　ちなみに、エクセルのブックオプション（計算方法）にある「表示桁数で計算する」というオプションにチェックを入れると、こうした現象は（たいていの場合は）出なくなります。なぜかというと、表示している程度に丸められてしまうため、「本当は1.8とイコールな値ではないもの」も1.8に丸められてしまうからです。

　というわけで、エクセル（に限らず）表示されてる値は「ホント」の値とイコールだとは限りません!?というのが、今日の教訓でした。･･･あるいは、単純明快で無いことをエクセルでやってはイケマセンというのが、本当の今日の教訓かもしれません。

■銃砲刀剣類所持等取締法で取り締まる「鉄砲」は「運動エネルギー」で決まります!?　

　銃砲刀剣類所持等取締法で取り締まる「鉄砲」は「運動エネルギー」で決まります!? を書きました。

　たとえば、密度11グラム/cm^3の鉛製の（計算しやすく）1cm角の弾丸を発射する器具があったなら、この弾丸を発射したとき２０ジュール以上の運動エネルギーを与えてしまうと、それはイコール「鉄砲」であるということになります。その「鉄砲か否か」となる境界値を計算してみると、秒速６０メートルとなります。つまり、1cm角の鉛弾丸を秒速６０メートルで打ち出す器具があれば、それは「銃砲刀剣類所持等取締法」で規制される「鉄砲」となるわけです。*

■磁力で色んなものを浮かべてみよう！　

　Levitron Revolution を買い、超手作りなサイコロもどきを空中に浮かべてみました。フンワリとものが浮かんでいるようすを眺めると、「静電場や静磁場を用いて、静止物体を安定に浮上させることは不可能である」という「アーンショウの定理」を知ってる人にとってこそ、不思議に楽しく感じられそうです。

　内部をスケルトンに眺めてみると。下の写真のようになります。浮いてる物体の中には磁石がいて、下部の床下には、（浮いてる磁石を引っ張る）リング磁石が１個と（リング磁石を浮かべ・位置制御するための）電磁石が４個隠れています。そして、装置中央にあるセンサで浮かせた磁石の位置をセンシングしつつ、電磁石の強さをフィードバック制御することで、静止浮上させるという仕組みです。

■幕末から明治にかけての浮世絵師「月岡芳年」の作品を３次元的に眺めてみよう!?　

　ColorDesigner（分光画像による超高精細・高忠実色再現画像の紹介）に、幕末から明治にかけての浮世絵師である月岡芳年の作品を、正面からや側面からと照明方向を変えて撮影した画像がありました。

　複数方向から照明を行った画像や、あるいは、複数方向から撮影した画像があれば、その画像を３次元的に眺めたようすを復元することができます。たとえば、浮世絵表面での反射のさまをCook-Torranceモデルとして仮定して（また、表面凹凸は、左右両側からの同時照明時と片側だけの照明時の違いから、適当に生成させて）、月岡芳年の浮世絵を３次元的に復元してみたのが下の動画です。

　黒い衣服の中の模様や、画面に時折配置された漆絵（うるしえ） っぽい艶のある黒部が、眺め方を変えるとリアルに光り輝き「浮かび上がってくる」のがわかるかと思います。黒一色に見える服に、実は緻密な（漆のような）光る模様が描かれていることが見てとれます。

　「漆や膠で血の色を出す」という派手な表現をしたともいう月岡芳年の浮き世絵を、こうやって色々眺めてみると面白いかも知れません。

　…芳年の絵に漆や膠で血の色を出して、見るからネバネバしているような血だらけのがある。この芳年の絵などが、当時の社会状態の表徴でした。

江戸か東京か「淡島寒月」

■見る方向で姿が変わるリアルな浮世絵を３次元的にグリグリ眺めてみよう!?　

　幕末から明治にかけての浮世絵師「月岡芳年」の作品を３次元的に眺めてみよう!? で月岡芳年の浮世絵の見え方を復元してみましたが、その復元結果を、Three.jsで色々眺めることができるようにしておきました。ポインタ操作やキー操作（Contrlなど）を使い、眺める位置を変えつつ眺めると、見る方向で姿が変わるリアルな浮世絵の姿が浮かび上がってきて、とても面白いかもしれません。

　参考までに、幕末から明治にかけての浮世絵師「月岡芳年」の作品を３次元的に眺めてみよう!?で行ったことをメモしておきます。物体表面の反射モデルは、その対象や近似の度合いに応じて種々あります。そのひとつ、Cook-Torrance+Lambertのモデルだと、表面各点の情報は、完全拡散の色情報を表す（たとえばRGB色空間だと）RGBの３スカラーと、表面の屈折率と表面粗さ（をある近似のもとに表すMicro facet係数）という、合計５つのスカラー量で表されます。逆に言うと、５つの未知数があります。さらには、版画に使われる材料では、その屈折率は高々1.5倍程度しか違わないので、屈折率については無視しても大差ないというわけで、未知数は高々４つになります。

　そこで、ColorDesigner（分光画像による超高精細・高忠実色再現画像の紹介）のような、正面・側面からと照明方向を変えて撮影した２画像があれば、各点に対してRGB画像×２という６つの情報が得られるので、先の５つ（もしくは４つ）の未知数を求めることができる、反射モデル（に必要な係数）を求めることができる、というわけです。

　複数方向から照明を行った画像や、あるいは、複数方向から撮影した画像があれば、その画像を３次元的に眺めたようすを復元することができます。

幕末から明治にかけての浮世絵師「月岡芳年」の作品を３次元的に眺めてみよう!?

■ゴッホの「星月夜」を３次元的にグリグリ眺めてみよう!?　

　「見る方向で姿が変わるリアルな浮世絵を３次元的にグリグリ眺めてみよう!?」では、ちょっと真面目に、幕末から明治にかけての浮世絵師「月岡芳年」の作品を３次元的にグリグリ眺めてみました。

　今日は、フィンセント・ファン・ゴッホの「星月夜（La nuit étoilée）」を、とてもテキトーに”グリグリ”眺めることができるようにしてみました。RGB画像を元にして、テキトーに凹凸データを作り、表面の粗さ分布もこれまたテキトーにでっちあげ、それらを重ね合わせて眺めてみました。

　いつか、超高解像度撮影画像に対して、”Synthesizing Oil Painting Surface Geometry from a Single Photograph”に書かれているような高品位に３次元レンダリングが可能な方法を試してみたいと思います。そうすれば、自分の手元で、凄くリアルに眺めることができる名画を作り出すこともできるかもしれません。

■「未知数”x”の語源はアラビア語という面白話」はデマの可能性が濃厚です!?　

　「未知数”x”の語源はアラビア語という面白話」はデマの可能性が濃厚です!?　を書きました。

　「方程式で未知数を”x”として表すことが一般的になったのはアラビア語に由来する」という話があります。xやyあるいはzといった文字で未知数を表し、a,b,c…といった文字で既知の値を表すのは、１７世紀に活躍したフランスの学者 デカルト が使い、その結果広まったとされる流儀です。この流儀の背景には、8世紀から15世紀にかけて盛んだったイスラム数学が反映されているという「へぇ〜。なるほど〜」と感じさせられる説明です。…この話は、さまざまな興味深いトークを開催しているTEDでもTerry Moore: Why is ‘x’ the unknown?として行われ、現在では非常に広まっています。

■「つよい」のに「人をいじめる悪いヤツだ!?」　

　”この中には「つよいでんき」が来ていますから「きけん」です。入らないで下さい”…と書かれた「立ち入り禁止」看板を見て、何だかガックリ気落ちしつつ考えました。
　「強い」イコール「正義の味方」という方程式を、遙か昔のゴールデンタイムのアニメで刷り込まれた世代としては、その正義の味方が、まさか人に危害を与える危険なヤツだったなんて…少し残念です。

　「弱電」「強電」とかいった言葉もあるくらいですから、「つよいでんき」もいれば、「よわいでんき」もいるのかもしれません。…しかし、「つよい」キャラクターは、人に優しい「きけんじゃない」存在だったらいいのに…、なんてクダらないことを考えます。

悪い人だ！シャアをいじめる、悪い人だ!!

■「オボった画像」で「自然なレイアウトの基本」を覚えておこう!?　

　「オボった画像」で「自然なレイアウトの基本」を覚えておこう!?を書きました。

　このスライドは、何年も前から使ってきたスライドなのですが、実はこのスライドには、少なくともひとつは明らかな「偽造」が行われています。つまり、「オボった箇所」があるのです。さて、一体どこに「偽造」が行われているかわかるでしょうか？

■情報理論で「胸」の「CG光源レンダリング」や「陰影の付け方」を学んでみよう！　

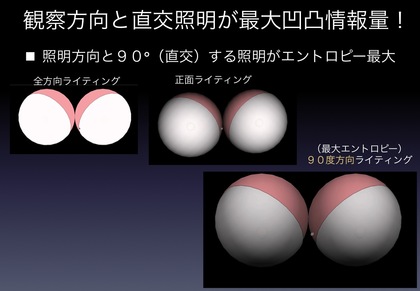
　情報理論で「胸」の「CG光源レンダリング」や「陰影の付け方」を学んでみよう！（上部直交２方向から照らすのが情報量＝エントロピー最大のバスト盛り上がり最大条件です!?）を書きました。

　実は、情報理論を使うと「バストの魅力を最大限に引き出すための光の当て方・陰影の付け方」を導き出すことができます。「バストの凹凸」も所詮は「情報」に過ぎないので…バストを映し出す・描き出した画像の「情報量（エントロピー）」を最大化する問題として捉えてみるわけです。

■ユニクロのUTme!で作る「掌周りの（疑似オッパイ計算用）空気流計算Tシャツ」　

　ユニクロのUTme!で掌周りの「空気流計算Tシャツ」を作ってみました。ナヴィエ・ストークス方程式も上書きした方がカッコイイかな？ と思いつつ、まずはとりあえずで方程式計算が教えてくれるメッセージを入れてみたのが、右の画像です。…こ・これは、思わず欲しくなってきたかも。

"Navier stokes equations tell us feeling of pseudo breasts!"

■赤い血が流れているはずの血管が青く見える理由　

　「青筋を立てる」という言葉で表されるように、皮膚上から見た血管は（周りの色と比べると）青色に見えます。「皮膚部分はメラニンスペクトルを反映し、静脈部分は皮膚部分と血液スペクトルの掛け合わせになるとしたら、静脈部分は近傍より（近傍を基準としても）赤く見えそうなのに、なぜ相対的に青く見えるのか」というのは、少し不思議に思えるはずです。
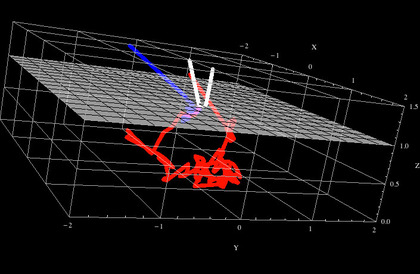
　この赤い血が流れているはずの血管が（血管の無い周囲部分よりも）青く見える理由を説明するために、以前書いたモンテカルロ光計算コードで、赤色光と青色光の軌跡例を計算してみました。下の図は、上から皮膚に差し込む光があると、青色光は皮膚内で（短波長の光は散乱しやすいので）すぐに散乱して・方向を変えまくり皮膚外部へ出て行ってしまうけれど、赤色光は皮膚内奥部まで侵入してから、皮膚の内部を長くさまよってから（ようやく）皮膚外へ出ていくという計算結果を表しています。

　こんな風に、青色光は皮膚内部にはほとんど侵入しないので、皮膚奥にある太い血管部分までは、実はほとんど到達しません。だから、血管がある（下部に）部分からも、血管がない部分からも、同じくらいの強さの（青色の）光が返ってきます。

　しかし、波長が長い赤色光は皮膚奥部まで侵入します。すると、皮膚下部に血管がある部分では、血管にまで到達し（血液が赤色をしているといっても、完全に透過するわけではないので）血管中で赤色光は減衰してしまいます。…そこで、皮膚下部に血管がある箇所では、青色光は他の部分と同じだけれど・赤色光は他の部分よりも暗い（少ない）というわけで、皮膚の上から見た血管部分は（近傍周囲と比較すると）青色がかって見えるわけです。

　皮膚の上から見た血管の（相対的な）色を決めているのは、実は血液の色ではなくて、その上にある皮膚の光散乱の波長依存の具合なのです。

■エクセルでラプラス方程式を解いて「血管がある皮膚周りの光強度分布」を計算してみよう!?　

　赤い血が流れているはずの血管が青く見える理由で行った計算を大雑把に解けば、たとえば完全拡散体として扱うことができます。それはすなわち、任意の微小領域が周囲に発する光強度は周囲（の微小部分が発する光強度）の平均値になるということで、つまりはラプラス方程式で表される解になります。

　…というわけで、ラプラス方程式を離散化して、お手軽なエクセルで「皮膚内部に血管がある時の、その周辺の皮膚内部・表面での光強度分布を（たとえば青色波長で）可視化してみたのが下図になります。エクセルの各セルは離散化された空間上の各領域を示していて、そこに示されている色と値が光強度を示しています。

　画面真ん中辺りに（画面＝シート鉛直方向に）血管が流れていて、画面＝シート上側にあたるのが皮膚表面です（画面下側が皮膚最奥部です）。

　さらに青色・赤色波長の「（光が散乱して方向を変えるまでの）平均自由行程」を踏まえて、表面での光強度分布の違いを描いてみると、限りなく大雑把な近似に基づいた計算をすると、下図のような感じです（縦軸はその波長における周辺近傍の平均強度を基準にした相対値です） 。

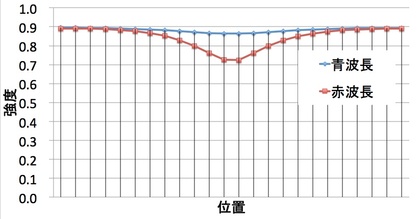
　血管が下部にある部分を眺めると、青色波長では、その周囲の部分とさほど変わらない光を発しています。けれど、そこを赤色波長で眺めれば（表皮近くの毛細血管ではなく）皮膚下部に流れる血液に光が吸収されて、光強度が（近傍周囲より）減少していることがわかるかと思います。…だから、赤い血が流れているはずの血管が（周囲に対して相対的に）青く見える、というわけです。

■いつだって「前」を見れば「n年前へ」の世界が見える！　

　hirax.netの全てのページには、「n年前へ」と書かれたリンク部があります。「記事」が書かれたのと「同じ月日」に書かれた、過去や未来の記事へのリンクです。n年前への「前へ」という言葉は、以前にあった過去を指すのか、それともこれから先にある未来を指すのか、それは今もってよくわかりません。それが、過去でも未来でも、とにかく「前へ」繋がっていることは１００パーセント間違いありません。

　そしてなぜだか「ｎ年分の過去」を眺めれば「ｎ年分の未来」を眺めることができる…と感じています。だから、n年分の過去や未来へ繋がるリンクには、何はともあれ「ｎ年前へ」という語句を書いておくのがふさわしい、というわけです。そういうわけで、hirax.netの全てのページには、「n年前へ」と書かれたリンク部を付けてあるのです。

　今日の「n年前へ」は、

• 今日のオッパイ・ウソ・ホント。（2001年）
• バンコクで眺めたPopular Electronicsと（Electronics NOW改め）Poptronics（2002年）
• 「狭い世界(せかい)」と「世間(せけん)が狭い」（2005年）
• 『専門家11人に「経済学」を聞く! 』と『11人いる!』（2008年）
• 七味唐辛子の「普通サイズ」と「大サイズ」の穴径は同じ（2009年）
• 「道具に使われるな！！道具は使うものだ！！」（2013年）

　「世界が狭い」と「世間が狭い」は180度違う。「狭い世界」を造り出すのは「知り合いが多いハブ的な人の存在」であり、「狭い世間」を造り出すのは、「周囲状況と繋がらず離れてしまっている人」である。「世界が狭い」は「広い世界」を引力が強い人がねじ曲げて色々な場所を繋げていた結果であり、「世間が狭い」は「広い世界」を知らず閉ざされている状況である。
　「世界が狭い」と「世間が狭い」は大違いなのだから、自分が考える「世界(というもの)」が、果たしてそれは「(自分の外に広がる広い)世界」なのかそれとも「(自分の周りの狭い)世間」なのかを問い直す作業が必要だと思う。

　小島寛之先生に、「10人の経済学者がいれば、11個の経済学説がある」という話を聞きました。その時、ふと「11人いる！」を思い出しました。あの話は「ロケットに乗ったのは10人のはずなのに、なぜか11人いる！」という話でした。「11人いる！」の結末は、「宇宙では思ってもいないことが起きる。必ず想定外のことが起きる。そんな時にどうするかが宇宙では重要だ」という感じだったように思います。

　…結局のところ、穴から出てくる粉体の量は、粉体の量とは無関係に、穴の大きさ（と粉体の密度）で表されることになる。たとえば、穴から出てくる粒子（＝七味唐辛子）は穴の大きさの３乗弱くらいに比例した量になる、という具合である。
　つまり、七味唐辛子の「普通サイズ」と「大サイズ」の穴径の大きさが同じなら、その二つの瓶から（一振りあたりに）出てくる七味唐辛子の量は同じになる。逆にいえば、大きいから瓶を一回振れば、たくさんの七味唐辛子が出てくるかというとそういうわけでないのである。

　…:多様性があって、変わらないところもあれば・変わるところもある。それこそが、（年齢ならぬヤング率で変化可能な度合いが決まる）弾性体だけじゃない粘弾性たる「おっぱい」ならぬ人間という存在なのかもしれないな。

　そしてなぜだか「ｎ年分の過去」を眺めれば「ｎ年分の未来」を眺めることができる…と感じています。だから、n年分の過去や未来へ繋がるリンクには、何はともあれ「ｎ年前へ」という語句を書いておくのがふさわしい、というわけです。そういうわけで、hirax.netの全てのページには、「n年前へ」と書かれたリンク部を付けてあるのです。

　今日の「n年前へ」は、

• 今日のオッパイ・ウソ・ホント。（2001年）
• バンコクで眺めたPopular Electronicsと（Electronics NOW改め）Poptronics（2002年）
• 「狭い世界(せかい)」と「世間(せけん)が狭い」（2005年）
• 『専門家11人に「経済学」を聞く! 』と『11人いる!』（2008年）
• 七味唐辛子の「普通サイズ」と「大サイズ」の穴径は同じ（2009年）
• 「道具に使われるな！！道具は使うものだ！！」（2013年）

　「世界が狭い」と「世間が狭い」は180度違う。「狭い世界」を造り出すのは「知り合いが多いハブ的な人の存在」であり、「狭い世間」を造り出すのは、「周囲状況と繋がらず離れてしまっている人」である。「世界が狭い」は「広い世界」を引力が強い人がねじ曲げて色々な場所を繋げていた結果であり、「世間が狭い」は「広い世界」を知らず閉ざされている状況である。
　「世界が狭い」と「世間が狭い」は大違いなのだから、自分が考える「世界(というもの)」が、果たしてそれは「(自分の外に広がる広い)世界」なのかそれとも「(自分の周りの狭い)世間」なのかを問い直す作業が必要だと思う。

　小島寛之先生に、「10人の経済学者がいれば、11個の経済学説がある」という話を聞きました。その時、ふと「11人いる！」を思い出しました。あの話は「ロケットに乗ったのは10人のはずなのに、なぜか11人いる！」という話でした。「11人いる！」の結末は、「宇宙では思ってもいないことが起きる。必ず想定外のことが起きる。そんな時にどうするかが宇宙では重要だ」という感じだったように思います。

　…結局のところ、穴から出てくる粉体の量は、粉体の量とは無関係に、穴の大きさ（と粉体の密度）で表されることになる。たとえば、穴から出てくる粒子（＝七味唐辛子）は穴の大きさの３乗弱くらいに比例した量になる、という具合である。
　つまり、七味唐辛子の「普通サイズ」と「大サイズ」の穴径の大きさが同じなら、その二つの瓶から（一振りあたりに）出てくる七味唐辛子の量は同じになる。逆にいえば、大きいから瓶を一回振れば、たくさんの七味唐辛子が出てくるかというとそういうわけでないのである。

　…:多様性があって、変わらないところもあれば・変わるところもある。それこそが、（年齢ならぬヤング率で変化可能な度合いが決まる）弾性体だけじゃない粘弾性たる「おっぱい」ならぬ人間という存在なのかもしれないな。

■「はやぶさ2と日本の宇宙開発」　

　春頃、JAXAのさまざまな方々にお話を伺う機会がありました。その時に伺ったお話の一部を、眺めることができるようになりました。

　たとえば、つくばのJAXA（旧NASDA）で日本のロケット開発に携わり続けた中村参与、長らく日本の固体燃料ロケットであるμロケット（旧ISAS）の開発を行っていた的川先生、次世代赤外線天文衛星スピカの中川先生…そういった先生が話された言葉を、少し眺めてみると、とても興味深いと思います。

　こうした本にしては少し変じゃない？と些細な違和感を感じさせる部分、こうしたムック書籍には全くもって不要に思える部分を、そここそを楽しんで頂ければ幸いです。

　米デルタ・ロケット技術が使われたN-1ロケットから、純国産技術で作られたH-Ⅱロケットを経て、こうのとりを打ち上げる最新のH-ⅡBロケットに至るまで、すべての成功は失敗に支えられている。

JAXA 中村参与

　H-IIBロケットのプロジェクトマネージャだった中村富久氏のお話を伺う機会があった。正直に、とても心動かされ・学ぶことが多かった。氏の手帳の最終頁には、「H−２A６号機失敗の教訓」という調査部会の報告が見返し続けるために貼られてた。

7:29 PM - 14 Apr 2014

　未来の日本のために、未来を作り出していくこどもたちのために、こどもに科学を「教える」ではなく「感じ取らせる」ことがとても大切だと思う。

糸川研究室の最後の大学院生でもあるJAXA的川名誉教授

　中身がわからない「ブラックボックス」が好きでなく、自分でコントロールしたい欲望がある。いかに目的に合い（特化し）・簡単に実現するかを、自分なりに追求している。座右の銘は、千利休の「人の行く、裏に道あり花の山。いずれを行くも、散る前に行け」

次世代赤外線天文衛星スピカの中川教授。

■おっぱいとエントロピー（動画比較と式変形過程）　

　情報理論で「胸」の「CG光源レンダリング」や「陰影の付け方」を学んでみよう！で例にあげた、完全等方照明下のおっぱいレンダリング例と・正面照明下のレンダリング例・最大エントロピー条件のレンダリング例を動画で見ることができるようにしました。また、途中で使った式変形も（この頁に）貼り付けておきます。

　下に貼り付けた式は、半球形状のバストモデルを２次元断面として（円筒断面として）扱い解析解を求めた上で、「３次元の場合は、とりあえず直交させときましょうか」という大雑把な扱いだけど、３次元空間での最適解を求める問題も、（全然役に立ちそうに無い）パズルとして面白いかも。