2016-01-17[n年前へ]
■エッシャーが作り出した３次元球体彫刻を「全天周投影」して眺めてみたい!? 
不思議な幾何学的世界を描いたオランダの画家エッシャーは、現実に触ることができる立体物つまり３次元体のアートも作り出しています。1940〜1950年代にエッシャーが作った３次元球体彫刻を眺めていると、なぜだか「あまり面白くない」と感じました。
その理由を考えると、３次元球体を眺めても、そのごく一部しか見通すことができないためではないか？と感じました。球体の表面に「空間を規則正しく埋め尽くす模様」が描かれていたとしても、部分的にしか「見えない」ために、２次元平面に描いた作品で感じるような「空間が不思議に意味を持った模様で埋め尽くされている」という印象を、ほとんど受けないのです。だから、今ひとつ面白く無い…と感じてしまうのではないか？と感じたのです。
空間表面を規則正しく充填する作品は、手に持てるような物体として表現するのではなく、自分を３６０度の全方向から包み込む（プラネタリウムのような）全天周画像として投影し、その世界の中に入り周囲４πステララジアンの空間全てが不思議な模様で連続的に埋め尽くされている風景を眺めた方が面白いような気がします。
「プラネタリウムドームに投影するエッシャーの世界」の上映会…眺めてみたいと感じる人・やってみたい！と思う人たちが少なからずいるのではないか？と想像してみたりします。
2016-01-18[n年前へ]
■「坂本龍馬」の白黒写真を機械学習でカラフルに眺めてみよう!?
CNN（Convolution Neural Network）機械学習による自動彩色（Google発のtensorFlowで実装した Automatic Colorization）に、約１５０年前に撮影された江戸時代末期の土佐藩志士「坂本龍馬」の白黒写真を入力させてみました。その結果得られた画像は、カラフルで生き生きとした…けれど少し昔の青年の顔です。（添付画像は彩度を上げたもの）
色情報を全く含まないはずの白黒フィルムに焼き込まれた風景や人の姿を、今やカラフルに「それっぽく」眺めることも簡単な時代です。たとえば、歴史の教科書に載っていたような白黒写真で覚えた人たちや風景を、カラフルに眺めてみるのも面白いような気がします。
そしてまた、こうした機械学習による「自動彩色」の例を眺めていると（たとえば自動彩色した「七人の侍」など）、手作業で行う最適化の苦労なんて、もう２０年近く前に終わったはずの２０世紀に置いてこないとダメな過去の遺物なんだった…ということを強く意識させられます。
2016-01-26[n年前へ]
■M.C.エッシャーのRelativity"を全天周で眺めてみよう!?
「手作りプラネタリウムと３D映像全国出張投影」の工房ヒゲキタさんに会いに、新宿２丁目近くの中華料理屋に行った。せっかくなので、以前から「M.C.エッシャーの立体世界を全天周プラネタリウムで眺めると面白いはず」と思っていたので、そんな雑談をするために３Dデータを（下に貼り付けた既存データを使って）作ってみた。
エッシャー自身も立体的なアート、周期的パターンが繰り返された球状の木製模型を作っていたりする。…けれど、それらは実際に眺めてみても結構つまらなく感じられてしまう。なぜかと言えば、そんな風に緻密に空間を埋め尽くしたアートであったとしても、そのごく一部しか眺めることができないとしたならば、新鮮さや面白さがほとんど消え失せてしまうからだ。
だとしたら、エッシャーの非現実かつ現実的な世界に３６０度全天周で入り込むことができればとても興味深いはず！というわけで、今朝は、幾何学的に無矛盾な "Relativity" を全天周で眺める準備をしてみた。幾何学的に無矛盾というのは、四方に配置された階段や壁は、そこに佇む人の向きが無重力で不思議なだけで、３次元空間的に特に不思議なところがあるわけではない、という意味だ。
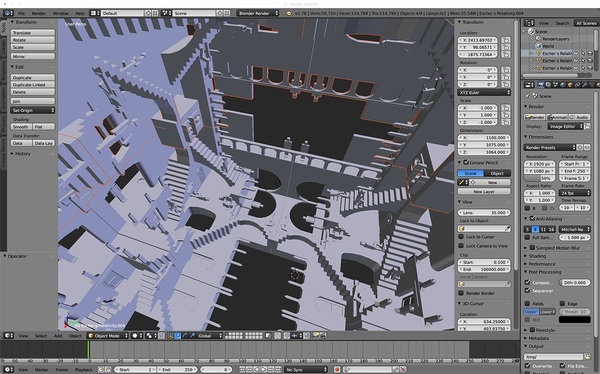
エッシャーが作り出した、非現実だけど妙にリアリティを備えた世界に入り込み、周囲の世界全てが奇妙に埋め尽くされていたとしたら…きっととても新鮮で楽しいと思う。M.C.エッシャーのRelativity"の世界は、全天周のプラネタリウムで眺めてみたら、絶対楽しいと思う。
2016-01-31[n年前へ]
■次元ネーミングから「自由度・情報量の価値」を考える
『篠崎愛の「匂いや吐息」をVRで“2.9次元”体験……バレンタインデーに開催』という記事に対する”4Dといい、みんな思い思いに次元数つけるなぁ・・・”というtweetを読み、何らかの自由度や情報量が増えることに対して、世の中は一体どんな次元ネーミング（値付け）をしているのか？が知りたくなりました。
そこで、そんな「○.×次元と自称するもののリストを作り、各自由度や情報量の（自称）価値を眺めてみました。このリストには、３次元プリンタのような「そのまんま」のものは、数勘定に含まないことにします。
- 2.1次元実装・2.5次元実装（基板積層の工夫は0.1〜0.5次元相当？）
- 2.5D印刷（数mm程度の凹凸は0.5次元相当？）
- 2.9次元バレンタイン（”「視覚」「聴覚」「触覚」「嗅覚」「味覚」の五感すべてで、限りなくリアル（3次元）に近い”）
- 4DX（動きや水・香りの追加は（２次元画像に対して）２次元相当？）
こうして眺めてみると、「2.9次元バレンタイン」が（２次元の画像情報に加えて）「聴覚」「触覚」「嗅覚」「味覚」が足されているにも関わらずわずか0.9次元しかプラスアルファとして数えられていないあたりが、次元数デフレというか何か数勘定が間違っているような気がしてきます。
」など。