hirax.net::inside out::2016年12月

■グラス片手に楽しく読めるシャンパンに関する計算や可視化解説　

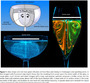
　普段はシャンパンなんて飲まないにも関わらず、クリスマスが近づくと風物詩的に少しだけ飲んでみたくなる。そんな時期に眺めてみるととても面白そうな「シャンパンに関する計算や可視化解説」があった。このConvective Mass Transfer in a Champagne Glass (Fabien Beaumont, Gérard Liger-Belair and Guillaume Polidori)が楽しいのは、登場する計算式が比較的簡単でわかりやすいということもあるけれど、何よりシャンパンが注がれたグラス内から立ち上る気泡を可視化したさまがとても美しく、その写真に思わず目を惹かれ、魅入られてしまうからだ。

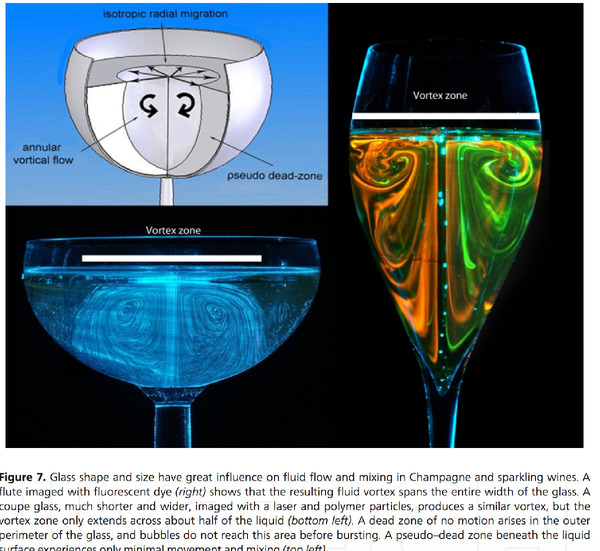
　アルゴンレーザーでシート状に光を照射して、シャンパンガラス周りでレーザー光が屈折してしまわないように、シャンパンを入れたグラスを水槽中に浮かべ、グラスを切断するように横から当てたレーザー光で浮かび上がらせた泡の動きは、ただ眺めているだけでも不思議に心地良くなる。

■「平面的に見える満月」と「立体的な月蝕」の秘密　

　太陽と正反対の空に浮かぶ満月は、とても平面的に見える。まるで、真っ平らな円を切り抜いて、夜空に貼り付けたように見える。白いピンポン球を手に持って、光を当てながら眺めたときのような、「中央近くは明るくて、周辺部分が滑らかに暗く落ち込む陰影が付いた、立体感ある見え方」にはならない。

　球の周りが徐々に暗くなる陰影は、物体表面に当たった光が、表面から外に帰っていく際に、周囲に等しく方向性を持たず返される時に生じる。そんな条件では、球の中心から端部までコサイン関数状の陰影が生じる。それでは、遙か古代に信じられていた平面状の月でなく、現実には３次元球体であるはずの月が陰影無く、真っ平らに見えてしまうのだろうか。

　その秘密は、月表面の反射特性にある。月の表面は、その表面を照らす光を、その光が発された方向へ返す性質があるからだ（Diffuse Reflections from Rough Surfaces ）。満月の時、月を基準にすると、月を照らす太陽は地球の後ろにある。そして、月を照らす太陽と同じ側に浮かぶ地球から月を眺めると、月の表面反射特性は「陰影がほとんどない、真っ平らな平面状の満月」を空に浮かび上がらせることになる。

　自分を照らす光を、その光が発された方向へと返す再帰性反射と呼ばれる性質は、急峻な凹凸の表面形状や（交通標識などで使われる）透明ビーズ（やキャッツアイ）など、多くの材質で現れる。再帰性の反射性質が現れる理由は、たとえば、前者の急峻な凹凸形状の場合であれば、斜めから当たる光も、表面が急峻な凹凸形状＊であれば、斜面（の法線方向に対し）垂直近くに光が当たり、その光が元来た方向へと帰って行きやすくなるからで、後者の透明ビーズでは、ビーン内部の反射により光が元いた場所へと戻っていくからだ。

　通常の満月がとても平面的に見える一方、同じ満月の時期に稀に訪れる皆既月蝕中の月は、とても立体的に見える。それは、太陽からの光を地球が遮りつつ、けれど地球大気が屈折させた太陽光は、月表面を見事なまでな立体的でグラデーション豊かな、名カメラマン顔負けの素晴らしいライティングとなる。

　次に日本で見ることができる皆既月蝕は2018年1月31日らしい。その満月を見ることができたなら、立体感溢れる月を眺めてみたいと思う。

---

＊そうした形状の表面反射を表したモデルが、Oren–Nayarの反射モデル

■「君の名は。」画風変換アプリをPython/OpenCVで書いてみよう! 〜意外に空変換は簡単? 編〜　

　先月下旬頃、映画「君の名は。」画風変換アプリEverfilterが流行っていた。軽く遊んでみた印象は、「空領域抽出処理に破綻が少なく（適切で）、その処理はおそらく普通の枯れた方法を使って、画面の４端辺から領域判定を独立にかけてる」ように感じられた。

　そこで、普通にやりそうなコードを書いてみたら、空領域抽出がどのくらいの品質が得られるか、確かめてみることにした。手っ取り早く試してみたいというわけで、Python/OpenCVコードを書いてみた。このコードは、入力画像と（入れ替え用の）空画像を読み込んで、グラフカットアルゴリズムが実装されたOpenCVのGrabCut関数を使い、（空がある程度の面積を占めていそうな）画面上半分の領域を対象として空領域を抽出し、その領域に空を合成するという処理を行うものだ。その処理例が、たとえば下に貼り付けた「バンコクの昼風景を夜空の下の街に入れ替えた画像」のようになる（上が入力画像、下が出力画像）。

　コードを書いて・試してみた印象は、OpenCVのGrabCut関数を使う程度でも、十分破綻の少ない空領域抽出を行うことができそうで、枯れた（枯れつつある）技術は便利だ！というものだ。実際のところ、「君の名は。」画風変換アプリ程度であれば、使用データ群（入れ替え用画像群）抽出処理も含めて、数日掛からず作ってしまいそうな気がする。

import cv2
import numpy as np

img = cv2.imread("bangkok1s.jpg")
mask = np.zeros(img.shape[:2],np.uint8)
skyimg = cv2.resize(cv2.imread("Starsinthesky.jpg"),
                         img.shape[1::-1]) 
bgdModel = np.zeros((1,65),np.float64)
fgdModel = np.zeros((1,65),np.float64)
rect = (0,0,img.shape[1],round(img.shape[0]*0.7))
cv2.grabCut(img,mask,rect,bgdModel,fgdModel,
                      50,cv2.GC_INIT_WITH_RECT)
mask2 = np.where((mask==2)|(mask==0),0,1).astype('uint8')
mask2 = cv2.blur(mask2,(5,5))
img2 = img*(1-mask2[:,:,np.newaxis])
skyimg = skyimg*mask2[:,:,np.newaxis]
img3 = cv2.addWeighted(skyimg, 1, img2, 1, 2.5)
cv2.imwrite("out.jpg",img3)
cv2.imshow("preview",img3)
cv2.waitKey()

■街通りを歩きながら…列車中で…似合う「飲料類」を決める振動動特性のヒミツ　

　街の通りを歩きながら、あるいは列車の中で1人飲み物を飲みたくなることがある。時にビール、あるいはコーヒー、その時の気分に応じた何かを手に持つカップに注いで飲んでみたくなる。とはいえ、カップから飲み物がこぼれたりするのはイヤだ…という人は、この論文 　"Damping of liquid sloshing by foams: from everyday observations to liquid transport"　を読んでみると面白いと思う。

　場所や状況に応じた飲み物を、その時の気分だけではなくて、その場所の「振動や揺れ」に応じて選びたい!と考える人に役立つこの論文は、飲み物の上面に浮かぶ「泡（foam）」が、どのように飲み物自体の揺れ・振動を抑える効果があるかを示している。液上面に泡がわずか数ミリメートルあるだけで、液面の揺れが数分の１に治まるようにすることができる現象解析をした論文だ。

　石けんや洗濯洗剤で「泡のかたまり」を作り、息を吹きかけたり・指で突き動かしたりすると、ブルブル震えて大きく揺れる。けれど、それと同時に、揺れがだんだん治まっていくことにも気付かされる。それはもちろん、たくさんの泡が「動き」を妨げるよう・緩やかにするよう抵抗として働くからだ。

　揺れが激しいところでは、きめ細やかな泡が厚く重なるギネスビールが似合う…とか、もう少し揺れが治まればピルスナービールが似合う…とか、（泡を持たない）コーヒーでは揺れが少ない落ち着いた場所が似合うとか、そんなことがわかる論文は、読んでみると面白いと思います。

■「（泡が下へ沈んでいく）ギネスカスケード」を高速度撮影してみよう!?　

　続々「（泡が下へ沈んでいく）ギネスカスケード」を近赤外線で撮影してみよう!?や過去ビール記事で書いたように、上が広がったグラスにビールを注ぎ、ビールの上面に溜まった泡を眺めると、きめ細やかにできあがった泡が下へ下へと下降しているさまが見えます。泡と言えば「上に浮かび上がっていく」ばかりに思えますが、いくつかの条件が重なると、グラスの中で「下へひたすら沈んでいく」ビールの泡を見ることができます。

　そんな「下降を続けるビールの泡」のようすを細かく確認するために、今日は高速度撮影を行っててみました。…といっても、やったことは、iPhoneに顕微鏡アタッチメントを付けて、標準機能の高速撮影を行ってみただけのことです。

　高速度撮影した映像を眺めてみると、泡（Bubble）というより遙かに密度が高く、むしろ泡（Foam）という言葉の方が適切かもしれない状態の中で、大きな泡は緩やかに下降して・小さな泡は隙間へと素早く動きながら速い速度で下降していることがわかります。ちなみに、この高速度撮影を行った時には、ビールグラスの中では「泡部分」と「ビール液体（だけがある部分）」は分離している状態になっています。

　これまでコンピュータ流体シミュレーションから予想されている現象は、グラス中央で浮かび上がる泡がグラス内部にビールの対流を生み、グラフの最外側境界で下降していくビールの流れに沿って泡が下降していくように見える、というものでした。しかし、ビールと泡がすでに分離したグラスの中で、泡が下降していくように見えるさまを眺めていると、もう少し違う説明も必要であるようにも思えてきます。

■Python/OpenCVで画像多重解像度解析コードを書いてみる　

　多重解像度解析…といっても直交基底に分解するというような話ではなくて、単に各周波数帯の特性がどの程度含まれるかを眺めるといった用途なら（つまり、ガボール変換やSTFTを掛ける感じの程度の用途なら）、Python/OpenCVを使って十数行で書けるかも？と思い書いてみました。もちろん、実装は簡単第一最優先！というわけで、ガウシアンフィルタ差分で２次元のバンドパスを作成し、それを周波数軸で重ねて眺めてみるというくらいの話です。

　実際に書いてみたら、ポスト処理含めて約２０行くらいになりました。超入門的な画像処理コードですが、１次元〜２次元の多重解像度解析や周波数解析を行うことは意外に多いような気もするので、適当に貼り付けておくことにします。＊

---

＊画像処理クラスタからのコメント：
　・マルチスケールで眺めるなら、DCゲイン1同士のガウシアン差分をとり、そのL2ノルムを1に正規化しすべし。
　・周波数軸は等比的にした上で、ボリューム的表示も等比的比率で重ねたい。

import numpy as np
import cv2
from matplotlib import pyplot as plt

def DOG(img, s, r):
    img2=img.astype('uint16')
    img2=img2*128+32767
    gs = cv2.GaussianBlur(img2,(0, 0), s)
    gl = cv2.GaussianBlur(img2,(0, 0), s*r)
    return cv2.absdiff(gs, gl)

img = cv2.imread("sample2.jpg",0 )
(h,w)=img.shape
pts1 = np.float32([[0,0],[w,0],[w,h],[0,h]])
pts2 = np.float32([[0,h*1/4],[w*3/4,h*1/4],
                   [w,h*3/4],[w*1/4,h*3/4]])
M = cv2.getPerspectiveTransform(pts1,pts2)
baseImg = cv2.warpPerspective(
    img.astype('uint16'),M,(w,h))

for i in range(100,5,-10):
    pts1 = np.float32([[0,0],[w,0],[w,h],[0,h]])
    pts2 = np.float32([[0+i,h*1/4-i],
    [w*3/4+i,h*1/4-i],[w+i,h*3/4-i],[w*1/4+i,h*3/4-i]])
    M = cv2.getPerspectiveTransform(pts1,pts2)
    img2 = cv2.warpPerspective(DOG(img, i, 1.05),M,(w,h))
    baseImg = cv2.addWeighted(baseImg, 0.9, img2, 0.3, 0)

plt.figure(figsize=(6,6))
plt.imshow(np.array(baseImg)) 
plt.autoscale(False)

■「π r2（パイアール２乗）＝面積」式は、ひいらぎ愛 さんの乳曲率に適用可能か？問題　

　「面積表示のタイトルがいいでしょ」というtweetに思わず目を引かれて、紹介文を眺めた途端に思わず笑ってしまいました。

「魅惑の巨大乳輪 ひいらぎ愛 π r2（パイアール２乗）＝面積１７６cm2」巨大乳輪に特化した新シリーズです。第一弾は乳輪直径15cm、面積176cm2の…

そして、ふと考えたのです。
「乳というものは、多くの場合は立体的な存在である。少なくとも、ひいらぎ愛さんの場合は、超立体的なものに違いない。それなのに、面積計算を２次元平面上の公式を使って良いものだろうか？」
そこで、果たしてπ r2（パイアール２乗）＝面積１７６cm2で良いのかどうか、軽く計算をしてみることにしました。

　ひいらぎ愛さんは、トップバストがバスト156cmでOカップということです。ということは、以前書いた おっぱい解析向けライブラリを使うと、彼女のトップバストに対してアンダーパストは45cm短い111cmであることがわかります。さらに、その乳を半球で近似した時の半径は30cmであると計算されます。

　乳を半球で近似すると、乳輪の面積は「半球を乳輪の大きさである立体角θで切り取った領域の表面積」となり、式で書くと、

　２π r^2 (1- Cos θ）

となります。立体角θは、「乳輪直径15cm」というのが、表面に沿って長さを計ったものだとすると、乳輪の立体角θは約２９度です。すると、その乳輪の表面積は172平方ｃｍとなります。π r2（パイアール２乗）から計算される177平方cmとは、約５平方ｃｍほど違います。最初の２桁だけを比べれば、曲率を考慮してもしなくても全く同じ数値ですから、その差は十分小さいのかもしれません。

　「π r2（パイアール２乗）＝面積」式は、ひいらぎ愛 さんの乳曲率に適用可能か？問題を解決するためには、その乳輪の直径だけでなく「円周の長さを計る」などの方法により乳表面の曲率を求める、という作戦が考えられます。それは、今後の課題としておこうかと思ます。