hirax.net::inside out::2017年12月

■安顕微鏡レンズを付けたスマホでレコードを撮影して音声化してみよう!?　

　最近のデジカメでレコードを撮影すると「レコード溝がクッキリ見える」という話を読んだ。ということは、”スマホでレコードを撮影すると音声再生するアプリができる時代が来そう”と思って呟くと、「思ったことは一体いつやるの！？今でしょ！今！」と諭された。…確かに、思ったことは、その時にやらないといつまで経っても何もできないような気もしてきます。

　そこで、ディスクユニオン横浜関内店に行くと、ちょうど「本日だけ！650円以下の全商品が100円！セール」をやっていたので、薬師丸ひろ子「セーラー服と機関銃」を買い、300円くらいの安い顕微鏡キットを付けたiPhone 6sでレコード溝を撮影してみました

　撮影手順は、静止画像で何枚も撮るのは面倒だったので、顕微鏡キットを取り付けたiPhone 6sを高速度撮影モードにして、レコードの上を滑らせながらの撮影です。そして、高速撮影動画を位置合わせ合成し、溝の太さをデジタル化することで、左右チャンネルを合成した音声ファイルを作成してみました。

　撮影した動画例は、下のようになります。実際には、レコード針が進む方向にとても長い画像ですが、左下の画像例は、それを圧縮したり・一部を拡大してみたものです。

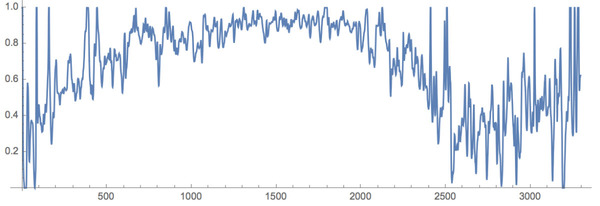
　デジタル化したレコード溝の太さを、グラフにしてみたものが、下の画像です。また、音声ファイル（WAV）化してみたものもここに置いておきます。
　今回処理してみたのは、とても短い時間分なので、音楽として聞こえるようなものではありません。けれど、普通のスマホ＋300円くらいで、アナログレコードの音声デジタル化撮影が（普通に？）できるようになっているのは、何だか少し面白いものです。

■史上最古？の円盤レコードを、画像処理で聴いてみよう!?　

　安顕微鏡レンズを付けたスマホでレコードを撮影して音声化してみよう!?で、顕微鏡キットを取り付けたiPhone 6sをレコードの上を滑らせて高速撮影からのデジタル化に挑戦してみました。

　こうした過去技術も数多くあったよね？と検索して見つけたのが、”media preservation／Extracting Audio from Pictures”です。これは、インディアナ大学ブルーミントン校のハーマン B ウェルス図書館にある棚、その奥にある本の395ページに印刷されていた印刷画像を見つけ、それが、最古に近い レコード「グラモフォン（1887年にエミール・ベルリナーが発明した円盤レコード）」であることを発見するとともに、その音声を画像処理的に復元した話です。

　この話は、素晴らしく面白い話です。何しろ、1877年にトーマス・エジソンが円筒形のレコードを発明し、その後の1887年にエミール・ベルリナーがに円盤レコードのグラモフォンを作り…といった、科学技術の歴史とともに、その復元を自分で（自分のコンピュータで、自分の手を動かして）確かめる・実感することができる、つまりは「楽しさ」が詰まっているからです

■Microsoft Excelで "=-1^2" が "-1"ではなくて"1"になる「理由」　

　Microsoft Excelで "=-1^2" が "-1"ではなくて"1"になるのが「なぜだろう？」というtweetを興味深く読み、そこから辿り着いた20年前のメーリングリスト記事が面白かったので、簡単なメモ書きをしてみます。メモ書きなので、面白い記事へのポインタと（その記事に対する）わずかな感想を書いただけの日記記事です。

　まず、この計算順にまつわる問題を考える時には、" Warning: Excel Performs Negation Before Exponentiation"のタイトルにもなっているように、Excelという一種のプログラミング環境上での、"negation"と"subtraction"という異なる2演算子の計算順序の違いを区別する必要があります。つまり、

=-A1^2

=1-A1^2

　次に、20世紀最後の年、つまり西暦2000年1月13日の20:18:46にDoctor Petersonがメールで書いている文面がとても参考になります。それは、"negation"のような単項演算子は”exponent”のような二項演算子に優先して演算されるものだったから、それをただ踏襲すると、こんな計算順序になるよね、というものです。「Lotus 1-2-3との互換性を重視した」わけではないけれど、プログラミング言語の過去経緯を踏まえて考える話だよね、というものです。

　そして何よりも、西暦2005年の12月16日にErikが書いているように、Windowsのメモ帳で "msgbox -2^2"と書いてから、そのファイルをtest.vbsという名前で保存して、もしもダブルクリックしたならば、（マイナス4ではなくて）"4"という答えが書かれたメッセージボックスを私たちは目にするよね。この例でもわかるように、エクセルの「ダメな話」として眺めるのではなくて、コンピューター科学の「興味深い話」として眺めるべき話じゃないか？というコメントが、とても参考になると思います。

So I think this isn't bad math on Excel's part, but good computer science.

■「月が欠ける向きは上下？左右？」…月の形で赤道や極への近さを意識する。　

　「スーパームーンより感動するタイの月を見逃すな」という記事を面白く読みました。それは、記事中のこんな一節に惹かれたからです。

　日本で見る半月は、満月から左（右）半分を切り取ったイメージなんですが、タイの半月は、「満月の上の半分を切り取った形」をしています。

　月が太陽に照らされて光る方向も、太陽から差し込む光が影になり「切り取られる」方向も、それはほとんど「月が空を進む方向」と一致しています。…正確には、太陽と月の軌道が約5度傾いているために、月が欠ける方向と進む方向にはズレがありますが、大雑把には同じです。

　すると、月が「欠ける方向」が、上下と左右どちらになるか…という問題は、空を月が進む方向が地平線となす角がどれだけか？…つまり、季節を無視すれば、月を眺める今いる場所が「赤道に近いか、（北極や南極といった）極に近いか？」という単純な問題になります。

　「スーパームーンより感動するタイの月を見逃すな」という記事を面白く読みました。それは、記事中のこんな一節に惹かれたからです。

　日本で見る半月は、満月から左（右）半分を切り取ったイメージなんですが、タイの半月は、「満月の上の半分を切り取った形」をしています。

　月が太陽に照らされて光る方向も、太陽から差し込む光が影になり「切り取られる」方向も、それはほとんど「月が空を進む方向」と一致しています。…正確には、太陽と月の軌道が約5度傾いているために、月が欠ける方向と進む方向にはズレがありますが、大雑把には同じです。

　すると、月が「欠ける方向」が、上下と左右どちらになるか…という問題は、空を月が進む方向が地平線となす角がどれだけか？…つまり、季節を無視すれば、月を眺める今いる場所が「赤道に近いか、（北極や南極といった）極に近いか？」という単純な問題になります。最初の記事で言うと、タイは日本より赤道に近いので、月は地平線から鉛直に近い方向に進み、月が欠ける方向も鉛直に近い（左右より上下に近い）…というわけです。

　少し面白いのは、日本の緯度は北緯約３５度…つまり、赤道と北極のどちらに近いか…といえば、むしろ赤道に近いということです。だから、昔から「上弦の月、下弦の月」というように、月が光ったり・欠けたりする方向を「上下」とも表現されてきました。

　けれど、今は、月が欠ける方向は「上下」ではなくてどちらかというと「左右」という認識も、自分の感覚を振り返ってみても、普通である気もします。…それがどうしてなのか、考えてみると、何だかとても面白い気がします。

■空を限りない青空にするスマホ版「偏光カメラ」を作ってみよう!?　

　3年半くらい前に作った（コンパクトデジカメを使った）偏光カメラを、スマホ版として作り直してみました。スマホに、秒24回転くらいの回転偏光フィルタユニットを取り付けることができるようにして、スマホを240コマ／秒くらいの高速撮影モードにすることで、秒24コマの特殊な動画撮影を行うことができるカメラを（今や一人一台誰もが持ちつつあるスマホを使って）仕立ててみた…というわけです。

　空を限りなく青空にして、そこにあるものの色を可能な限り純色にする、そんな特殊な動画撮影を、ほぼ全てのスマホで行うことができるようになります。一体どんな特殊撮影が可能になるかというと…たとえば、下に貼り付けた画像は、普通に撮影した画像（左）と映り込みを極限まで減らして、色をできるだけ鮮やかにした画像（右）の例です。

　右上の画像では、物体表面の散乱反射光が（可能な限り）減らされています。つまり、空気の中で生じる光散乱光をとても減らした結果、まるで「空気が無い宇宙空間に、街が佇んでいる」ような、「昼間のような、夜間のような」…不思議な街景色になっていることがわかります。

　色鮮やかにするだけでなく、たとえば下に貼り付けた動画のように、その他にも色んなことができます。…けれど、そんなエトセトラは、また週末にでも遊んでみることにしようと思います。