hirax.net::Keywords::「アルキメデス」のブログ

■アルキメデスのパンチラの式　

「スカート円錐」の明るさを探れ

「スカート円錐」の明るさを探れ

　以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性（別に男性でも構わないが…）の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。

　その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。


　ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。

　しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか？角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて（たぶん）かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が（見えるくらいに）十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。


　まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか？

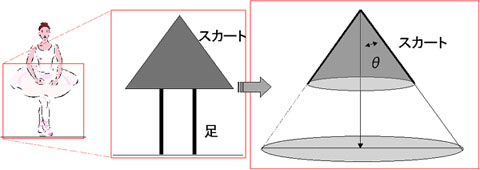　もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか？」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか？」ということを考えることと同じなのである。

　そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心（つまりはスカートの中の下着部分だ）にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。


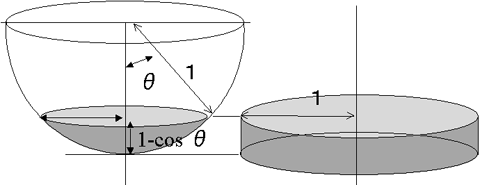　つまり、角度Θで広がるスカートの中が「どれくらい明るいか？」という疑問は、「下図で色を付けた部分球の面積はどのくらいか？」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か？」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。

　ところで、アルキメデスが発見したように、球（もしくはその一部）の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような（色を付けた）円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は

円筒の面積 = 2 π (1-cosΘ)

であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は

という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式（ここでは仮に『パンチラの式』とでも呼ぶことにする）」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。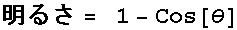

　試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを１とした時の「スカートの中の明るさ」を示しているのである。

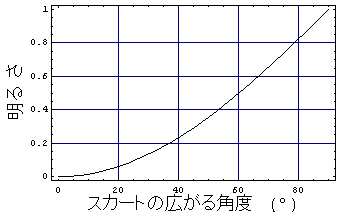　基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。


　ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば（例えば床の明るさの5%程度にでも明るければ）、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない（ハズだ）。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所（例えば照明や、照明に照らされた明るい壁）だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。

　例えば、下の画像は周りの明るさに対して、

1. 5%の明るさ
2. 10%の明るさ
3. 20%の明るさ

を持つ三種類のロゴである。この三つの画像を眺めてみれば、明るさが5%のものはなかなか判別しにくいが、20%以上の明るさのものであれば比較的容易に判別できることが判るだろう。明るいものが視野に入っている限りは、人間の目は「一番明るいものの10%以下程度の明るさのモノ」はなかなか識別することはできないのである。

5 %

10 %

20 %

　ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床（や照明や壁）などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。

　というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。

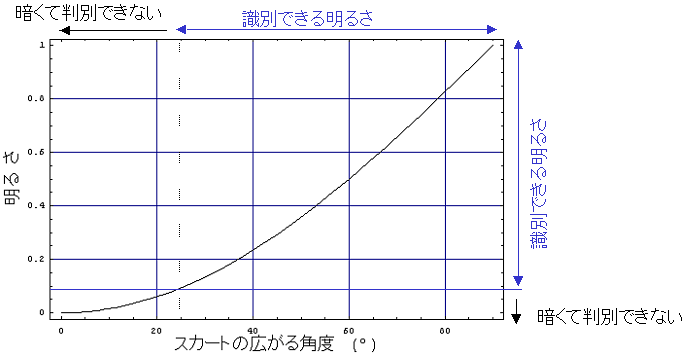　つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。


　例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は（人間の目からすると）真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。

　ところが逆に、床が白かったりして明るいクセ（つまり下からの照明が強いクセ）に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で（下から）スカートの中を覗かれたりしてしまうと、（下から覗く人の視界に入る）周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。

　
　ところで、今回は「スカートの中の明るさを示す＝パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし（全然役に立たないような気もするが）、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い（？）のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。

■人類が月面上で日常を過ごす時代…それは「あのイタズラが成功する日」かもしれない？　

　その辺の人（@create_clock） さんのtweetが面白かった。

マンガとかで教室の引き戸に黒板消しを挟んで開けると頭の上に！みたいな描写があるけど、実際にやったことのない人の描写だなと思う。黒板消しの落ちるタイミングが早すぎて頭には当たらない。

10:08 PM - 25 Jun 2018

　…確かに、実際にやった過去を振り返ると、黒板消しの落ちるタイミングは早すぎて、誰の頭にも当たらなかった。

　計算をしてみるとこうなる。教室の入り口の高さは、約2メートル。そこに黒板消しを挟み、ターゲットを待ち構える。ターゲットがドアを開け、身長1.7メートルのターゲットの頭の高さに黒板消しが落ちるまでの時間は、わずか4分の1秒の0.25秒。…そんな短時間に、教室のドアを開け、ドアの真下を通過するのは確かに無理に違いない。

　もしも、もうひとつの世界があったとしたらどうだろう？…「教室の引き戸に黒板消しを挟んで開けると頭の上に当たる」…そんなもう一つの世界線、もっと別の場所があったとしたならば、そこは一体どんな場所なんだろうか。

　たとえば、教室のドアを開け、ドアの真下に移動するまで、1.5秒掛かるものとしてみる。…もしも、その世界が地球と同じような惑星・密度の場所だとしたら、その惑星の半径は約1900キロメートルという計算になる。そういう星の上で生まれたのなら、「教室の引き戸に黒板消しを挟んで開けると頭の上に落ちる」イタズラができることになる。

　もしも、その星の密度が地球と違ったらどうだろう？地表での黒板消しが「頭の高さまで落下する時間」が0.25秒だとして、「教室のドアを開け、ドアの真下に移動するまでの自然な時間、1.5秒」は、ちょうどその6倍に近い。…すると、たとえば、主人公が暮らす世界線がもしも（地球表面比で重力が1/6の）月面上だったとしたら、計算が合うことになる。つまり、教室のドアを開けてから、身長1.7メートルの主人公の頭に黒板消しがあたるまでの時間が、ちょうど1.5秒後…という計算になる。

　そうか！そうだったんだ！…ぼくらが昔から眺めたあの景色、「教室の引き戸に黒板消しを挟んで開けると頭の上に落ちる」は決して過去の懐かしい「三丁目の夕日」的な昭和の懐かし風景ではなく、あれは人類が月面上で日常を過ごす遙か未来の日常風景を蜃気楼のように眺めていたに違いない！と気がついた。

　そんな発券をしてEureka（エウレカ）！とアルキメデスのように叫び、その瞬間に夢から覚めた。…重力が1/6の世界で、「教室のドアを開けてからわずか1.5秒でドアの真下に移動することは難しい」かもしれない。「教室の引き戸に黒板消しを挟んで開けると頭の上に当たる」…そんなもう一つの世界線は、一体どんな宇宙にあるんだろうか。