1999-11-20[n年前へ]
■バナー画像のエントロピー 
がんばれ、JPEG
前回、
で「バナー画像中の文字数とファイルサイズ」に注目し、「文字情報密度」というものについて考えてみた。情報密度を考えるのならば、で考えたエントロピーについても計算してみなければならないだろう。そこで、今回は前回登場したバナー画像達のエントロピーを計算してみることにした。それにより、情報圧縮度について考えてみることにするのだ。
そうそう、今回も「本ページは(変な解説付きの)リンクページであります」ということにしておく。他WEBのバナー画像を沢山貼っているが、それはこのページが「リンクページ」であるからだ。
エントロピーを計算し、画像の圧縮度を調べる際に、今回はファイル先頭の400Byteにのみ注目した。ファイル全体で計算するのは面倒だったからである。各バナー画像でファイルサイズが異なるからだ。そこで、全て先頭400Byteに揃えてみた。
行う作業は以下のようになる。
まずは、画像ファイルの「先頭400Byteの可視化画像」を作成する。これは、各ファイル中の各Byteが8bitグレイ画像であると考えて、可視化したものである。以前書いたように、「てんでばらばらに見えるものは冗長性が低く、逆に同じ色が続くようなものは冗長性が高い」のである。もし、同じ色が続くとしたならば、「また、この色かい。どうせ、次もこの色なんだろ。」となってしまう。次の色の想像がつく、ということはすなわち、情報としては新鮮みのないものとなる。つまり、情報量が少ないのである。その逆に、情報量の多いものは、てんでばらばらで次の色(データ)の予想がつきづらいもの、となるわけである。まずは、そのてんでばらばら具合を「先頭400Byteの可視化画像」で確認する。
次に、てんでばらばら具合をヒストグラムで確認する。各Byteが0から255のどの値をとることが多いかを調べるのである。てんでばらばらであれば、どの値をとる確率もほぼ同じであり、フラットなヒストグラムになるはずである。逆に、ヒストグラム上である値に偏っていれば、値の予想がつきやすく、情報量が少ないということになるわけだ。
最後に、各Byteのデータを「8元無記憶情報源モデル」に基づいて計算したエントロピーを計算した。各Byteのエントロピー、すなわち、平均情報量は最大で8となる。当たり前である。1Byteは8bitであるから、最大限有効に使いきれば、情報量は8bitになる。
それでは、青い「hirax.net できるかな?」バナーを例にして見てみる。
| 文字情報密度 | ファイルサイズ(Bytes) | 画像 | 先頭800Byteの可視化画像 | ヒストグラム | エントロピー(bits/Byte) |
| 35 | 662 | 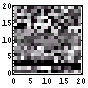 |  | 7.1 |
この画像ファイルはトータルで662Bytesであるが、その先頭400Bytesの可視化画像はけっこうばらばらである。それは、ヒストグラムをみても確認できる。少し、0近傍が突出しているが、それを除けば、かなり均等である。そして、エントロピー、すなわち、1Byte当たりの情報量は7.1bitである。満点で8bitであるから、7.1bitはなかなかのモノだろう。
それでは、前回登場したバナー画像達に、同じ作業をかけてみる。
| 文字情報密度 | ファイルサイズ(Bytes) | 画像 | 先頭400Byteの可視化画像 | ヒストグラム | エントロピー(bits/Byte) |
| 31 | 874 |  |  | 6.7 | |
| 34 | 648 | 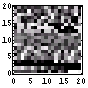 |  | 7.2 | |
| 35 | 662 |  |  | 7.1 | |
| 40 | 763 |  | 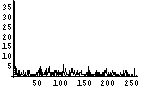 | 7.1 | |
| 44 | 1003 |  |  | 7.1 | |
| 54 | 750 |  | 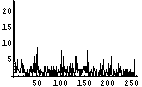 | 7.1 | |
| 58 | 864 |  |  | 6.6 | |
| 112 | 2472 | 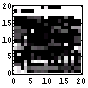 |  | 3.8 | |
| 124 | 2348 | 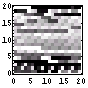 |  | 7.0 | |
| 155 | 465 |  |  | 7.3 | |
| 223 | 3116 |  | 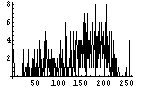 | 7.0 | |
| 294 | 881 | 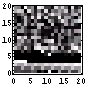 |  | 6.6 |
IntenetExplorer、RealPlayerといった、ヒストグラム上で突出している値がある画像はエントロピーが少ない。すなわち、平均情報量が少ない。大体、6bit台である。gooは0近傍の値が突出しているのが足を引っ張り、6.6bitとなっている。これらは、1Byteの8bit中の1bit強が無駄となっているわけである。
最高点はMacの7.3bitである。8bit中で7.3bitの情報量を持っているのである。逆に言えば、0.7bitは無駄ということになる。しかし、8bit中7.3bit使い切っているのはなかなかのものである。
それ以外は大体7bit台で拮抗している。しかし、それはいずれもGIF画像である。そう、唯一のJPEG画像である「今日の必ずトクする一言」が3.8bitと低い情報量であるのだ。しかし、これには、いろいろな理由があると思われる。例えば、ファイル全体ではなく先頭のみを見ているため、JPEGのヘッダー部分が入ってしまい、冗長性が高くなってしまっている、とかである。全体でなく、部分で評価しているのは非常にマズイだろう。また、GIFが情報圧縮していることもあるだろう。そのため、JPEG陣営にはかなり不利であったと思われる。
そうそう、今回は情報圧縮度にだけ注目したから、JPEGに不利な結果になった。けれど、他のいろいろな理由を挙げれば、GIFは使いたくないという気持ちもあるのだけれどね。けど、便利なんだよね。
2000-01-27[n年前へ]
■「富士の樹海」を目指せ 
磁界を可視化しよう
以前から探していた「面白いもの」を入手した。この写真がその「面白いもの」なのであるが、何だかわかるだろうか? ちなみに、大きさは「1cm×5cm」位のシートである。
 |
これは「マグネビュアー」というものである。磁界を可視化してくれるシートだ。マイラーフィルムの間に磁性体を混入させたマイクロカプセルを入れることで、磁界に対する配向性を持たせたものだ。と、言葉でいってもなかなかわかりにくいので、磁界を可視化した写真を示してみる。何しろ、百聞は一見に如かずである。
次の写真は某ピザ店のマグネットシート(よく冷蔵庫の扉に張り付ける奴)の上に「マグネビュアー」をのせたところである。ピザ屋は私の食生活を支えていると言っても良い。私が生きているのはピザ屋のおかげである。
 |
私の「命の恩人」でもある某ピザ店のマグネットシートがつくる磁界が見て取れるだろう。磁界が可視化されているのである。
本WEBではこれまで様々な「可視化」で遊んできた。例えば、
- 感温液晶でNotePCの発熱分布を可視化する
- ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- 恋の力学 -恋の無限摂動 - (1999.12.21)
- WEBサイトの絆 - WEBの世界を可視化しよう- (2000.01.13)
- 夜のバットマン - 超音波を可視化しよう- (2000.01.17)
上に示した「某ピザ店のマグネットシートの表面」の磁界の様子も面白いが、もっと面白いのは「某ピザ店のマグネットシートの境界」の磁界を可視化したものである。
それが下の写真である。磁界の様子が実感できるのではないだろうか?
 |
下に示す図はドーナツ型の磁石の周りの磁界をCUPSを用いてシミュレーション計算した結果である。この計算結果と同じようなものが「マグネビュアー」を使うと簡単に可視化できる。
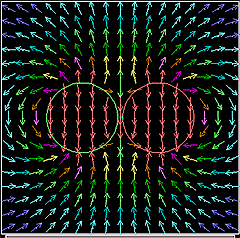 |
普通、こういった磁界の可視化は磁気造影剤や砂鉄みたいな磁性体粒子を用いるのであるが、そういったものはどうにもハンドリング性にかける。液体や粉体などを家の中で実験に使うのはイヤである。いや、もちろん仕事で使うのもイヤであるが... そこで、この「マグネビュアー」が登場するわけだ。
それでは、その他の面白そうな磁界を可視化してみたい。磁界と言えば、やはりアレの登場だろう。もちろん、アレと言えば磁気カードである。クレジットカードや銀行のキャッシュカードといった磁気カードだ。一例を次に示してみる。こんなヤツだ。
 |
カードの下に黒い磁気データ記録部があるのがわかるだろう。
それでは、その「磁気データ記録部」に「マグネビュアー」をのせてみよう。はたして、磁気データは可視化されるだろうか?
 |
といっても、この写真ではわかりにくいので、「マグネビュアー」を拡大してみよう。すると、バーコードのような模様が見えるのがわかると思う。「磁気データ」が簡単に可視化されているわけである。この「マグネビュアー」と普通のスキャナーがあれば磁気データ読み取り機がなくても磁気データが読みとれるのである。
 |
しかし、このカードに関しては内容を解析するとマズイ事情があるので、次回に「ソフマップ」のカードを題材にして磁気カードの内容を可視化してみるつもりだ。題して、
- ソフマップでお買い物 - 磁界の可視化とバーコード - (仮称)
さて、話は変わるが、私はこの「マグネビュアー」を手に「富士の樹海」を目指すつもりだ。「富士の樹海」では」方位磁針が変な方向を示すと伝えられている。そしてまた「富士の麓」ではとかく人は判断を誤りやすいとも聞く。船頭多くして船山に登ると言うが、「富士の樹海」には判断を誤った船が沈没しまくりである。
私は「富士の樹海」の真実をこの「マグネビュアー」で明らかにするつもりだ。「富士の樹海」の謎を明らかにするのである。何故、方位がそして人が判断を誤るのか、その謎を明らかにするのだ。
しかし、もしも、もしも、の話であるが、本WEBの更新が止まった際には、「富士の樹海」で私が眠っていると思って欲しい。「マグネビュアー」が役に立たないはずがないのだが、きっと何か判断を間違えたのであろう。そうそう、あくまで「富士の樹海」である。「富士の裾野」ではないので念のため...
2000-09-02[n年前へ]
■もうすぐ二歳の「できるかな?」 
初心に帰ってみましょうか?
「できるかな?」が始まったのは二年近く前の秋のことだった。
でも触れたが、当初(実は今も続いているが)は某社内の某サーバー内でこっそりと始めてみたのだった。それから二年あまりでずいぶんと色々な話が増えた。某社サーバー内でしかアップしていない- プリンタドライバーは仮免
- 続 電子写真プロセスを分数階微分で解いてみよう
- 続々 電子写真プロセスを分数階微分で解いてみよう
そして話が増えてきたせいか、自分自身でも「アレッ、あの話はどこにあったけ?」というように迷ってしまうことが多々ある。迷うどころか、最後まで見つからないこともしばしばあるのだ。そして、それは私でもない他の人であればましてやそうだろう。というわけで、
では簡単にそれまでの話の紹介をしたし、ではhirax.net内の全文検索機能を付けてみた。今回は、これまでの話題をもう一度自分で読み直して、その中から「自分のお気に入り」を調べてみたいと思う。そして、最近少し話題が変になってしまっている反省をして、もう一度初心に帰ってみようと思うのだ。
まずは、1998年の話題からいくと
というあたりが、良い感じだ。京都の風物詩である「鴨川カップル」達が人目を気にしながら寄り添う合う姿を考えてみたものだ。後の「恋の力学」シリーズなどはここらへんから始まっていた、といっても良いだろう。そしてこの頃の[Scraps]系の話題としては、がある。少し前に、この「さなえちゃん」を描いた漫画の作者からメールを頂いたのがとても私には印象深かった。そして、1999年の上半期から選んでみると、まずは
というところだろう。ハードディスクの情報を可視化することで情報圧縮・エントロピーを考えてみた一話である。そして、同じような「可視化シリーズ」の一つである- 感温液晶でNotePCの発熱分布を可視化する- 熱いところで感じてみたい St.Valentine 記念 - (1999.02.14)
- NotePCの発熱分布を比べてみたい- お熱いのがお好き SOME LIKE IT HOT - (1999.02.15)
そして、1999年の下半期はもう自分で言うのも何だが傑作揃いである。大体、書いているペースが自分でも驚くくらいのハイペースだ。月当たりの話の数を数えてみると、
- 7月 9話
- 8月 9話
- 9月 8話
- 10月 8話
- 11月 11話
- 12月 9話
この頃の「お薦めの話」はいっぱいある。例えば、
に始まった「文章可視化シリーズ」や、で始まった「ASCIIアートシリーズ」だろう。から始まる「江戸五色不動シリーズ」は江戸にロケまで行ったので、とても思い出深い話の一つである。しかも、妙な偶然のせいでまるで小説の中に迷い込んだような気持ちになったものだ。そして、WEBページを作る上では
などもどうしても外せない。そして、この後結構続くことになるという「恋の力学」シリーズもこの時期に始まっている。そして、この頃の一番人気が何と言ってもだろう。この「ミニスカート」系の話の流れは以降も続くことになるのが自分では意外でもあり、残念でもある。それはさておき、ナンセンス系ではなんてのも面白い話だと思う。そして、1999年の終わりはやはりこれが「お気に入り」の話である。また、[Scraps]系の話がこの時期にはやたらいっぱいあるのが面白いところだ。その内からいくつかピックアップするとこんな感じだろうか?- [Scraps]絵馬 - どこにもいないよ- (1999.07.09)
- 新宿駅は電気羊の夢を見るか- 意識とは何か - (1999.07.10)
- [Scraps]合掌 - キレイはキタナイ、キタナイはキレイ- (1999.08.01)
- [Scraps]いつかきっと -掌の中の答え - (99.11.03)
- 「文学論」と光学系 - 漱石の面白さ-(2000.02.27)
- 恋の力学 恋の相関分析編- 「明暗」の登場人物達の行方 - (2000.04.01)
- 恋の力学 恋のグラフ配置編- 「明暗」の収束を見てみよう - (2000.04.02)
- 恋する心を見てみたい - 恋のきっかけはどの出来事?- (2000.05.14)
- 恋の形を見た人は - 恋の相対性理論- (2000.05.17)
さて、今回は2000年上半期までの話の中から「私の好きな話」を振り返ってみた。とはいえ、私の好きな話=他の人の好きな話ではないようだし、他の話も適当に眺めて頂いたら良いかなぁ(私が)、と思うのだった。
2003-10-24[n年前へ]
■エントロピー・ゼロの恋 
「エントロピーは乱雑さ・混沌さ・わからなさなどの程度を示す量であるから、好きな相手に告白をするということはエントロピーを減少させる」という「エントロピー零の恋」
友人はうちあけて振られたけれど、大学卒業して1年後には別な人と結婚してしまった。やはり、エントロピーを減少させるということは、勇気ある人の行なえることかも知れない。一方、若き私はエントロピーを零にしない生き方を好んだ。彼女にうちあけて返事を聞いてしまったら、不運にも振られたらもちろんであるが、幸運にも相手が自分を好きであったとしても、そこでせつない恋愛は終わりである。恋愛の本質はせつなさにあると考える私などは、エントロピー零の恋に情緒を感じない時代遅れの男だった。この他の「数学的思考(?)エッセイ」もオススメです。数学だって物理学だって経済学だってどんな学問もきっと楽しいんだろうなぁ、と思わせるこれらのコンテンツ、眠れぬ夜のお供にいかが?
2003-11-04[n年前へ]
■「クロスエントロピーに基づくネットワークの可視化技術」 
クロスエントロピーに基づいて定義されるエネルギーを最小化することによって、ブラウジングに適したわかりやすい可視化を実現。メリットとしては、各ノードが重ならない、部分切り出し再配置も安定。 from NTTコミュニケーション科学基礎研究所 CS企画