2000-10-25[n年前へ]
■虹の彼方に。 
色覚モドキソフトを作る その7
今年は好きなWEBサイトがいくつも店じまいしてしまった。「わきめも」もそんなサイトの一つだ。その今はもうない「わきめも」の中で、きれいな虹が見えた。だからビールを飲んだ。だけど、目に見えている虹の色は写真のフィルムには写らない。どんなフィルム・CRT・プリンターの出力色空間もとても狭くて、虹の中に見える色は出せないからだ。ビールも虹も「生」に限る。という話があった。もう元のWEBページがあるわけじゃないから、細かいところは違っていたかもしれないけれど、大雑把な内容はこんな感じだった。- ビールも虹も「生」に限る - なんてとてもシブイセリフで良い感じだ。
このセリフの中の「どんなフィルム・CRT・プリンターの出力色空間もとても狭くて、虹の中に見える色は出せないからだ。」というのを図示してみると、下の図のようになる。
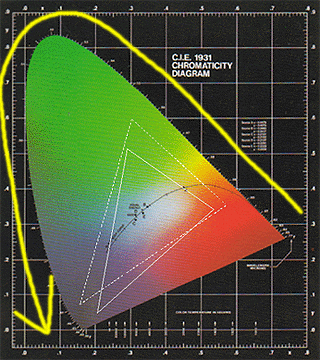 |
例えば、虹の中に見えるスペクトル色はこの図で言うと、黄色の矢印で描いた側の、色で塗りつぶした領域の外枠の色だ。波長の長い単色光、つまり最初は赤色から始まって、波長が短くなるに従い「赤→黄色→緑→青→紫」というようにスペクトル色はつながっている。
この図中に、とあるCRTとプリンターの出力可能な色空間(CCMファイル中に埋め込まれているプロファイル情報を参考にしたもの)を白点線と白実線で示したが、とても狭い領域の色しか出せず、とてもじゃないが虹の中に見えるスペクトル色はこれらの機器では出ないことが判るだろう。
だから、「生」の虹を見たときの感じは写真でもCRTでもプリンターの出力でも味わえないわけだ。おいしいビールは「生」に限る(私の趣味では)のと同じく、虹も「生」に限るのだ。
だから、虹の色と同じ
の時に撮影したような太陽光のスペクトルも、こんな風にWEBページの上で眺めても、それはやっぱり分光器を「生」で覗いている感じはとてもじゃないが味わえない。 |
こんな、「赤→黄色→緑→青→紫」というスペクトル色を眺めていると、中学の頃の美術の授業を思い出した。その授業の中で、こんな色相環が教科書か何かに載っていて、「こんな色のつながりは「赤→黄色→緑→青→紫」というスペクトル色に対応しているんだよ」と美術の先生に言われた。それを聞いていた私はよく判らなくなって、「すると、何で紫と赤のところで繋がってるのでしょうか??」と先生に聞くと、その先生も「う〜ん。」と悩み始め、しまいには「いつか調べて答えが判ったら、私にも教えてくれたまえ。」と言うのである。今考えてみると、それはとても素晴らしい言葉だった(間違っても皮肉でなくて、本当に素晴らしいと思うのだ)。
 色覚のメカニズム 内川恵二 朝倉書店 口絵より |
だけど、「赤→黄色→緑→青→紫」という単色光のスペクトルが波長としては単に一方向に変化していくだけなのに、グルっと一周する感覚を受けるのはとても不思議である。そこで、色感覚モドキソフトを作ってそこらへんの感覚を眺めてみる、つまり「できるかな?」の常套手段である「その謎を見てみよう」と思うのである。
この「色感覚モドキソフト」はいつものように極めて大雑把でチャチな作りである。ソフトの流れとしては次に示すように、
1.光源としては二種類の場合
- RGBのCRTモニタ
- 単色スペクトル光
2.画像を読み込み、画像の任意の場所のRGB値を元に光全体としてのスペクトルを計算する。
3.錐体の分光感度を適当に設定し、Boynton色覚モデルをもとに
- 「赤<->緑」チャンネル
「青<->黄」チャンネル
「輝度」チャンネル
ここに今回作成したtruecolor7を置いておく。細かい使い方は今回は割愛したい。が、多分少し使えば(使う人がいるともそうそう思えないが)、使い方はすぐに判ると思う。
- truecolor7.lzh 522KB
truecolor7の動作画面はこんな感じである。
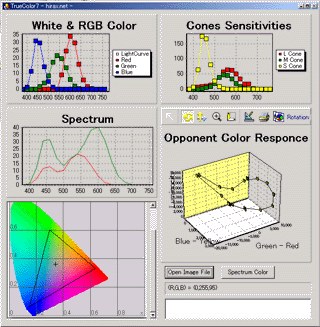 |
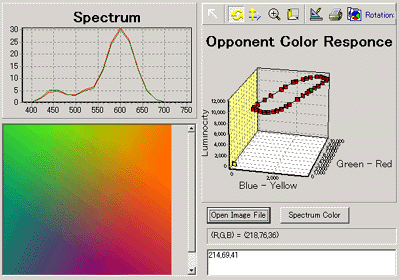
左上から下に向かって、RGBそれぞれのスペクトル設定、全体でのスペクトル、読み込んだ画像、右上から、錐体の分光感度、反対色応答の出力値である。
画像の任意の場所を調べたければ、BMP画像を読み込んでマウスで好きな場所をなぞるなり、クリックすればよいし、「赤→黄色→緑→青→紫」という単色光のスペクトル色の場合を計算したければ、右下にある「SpectrumColor」ボタンを押せば良い。
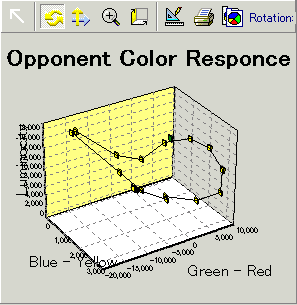
さっそく、赤→黄色→緑→青→紫というスペクトル色の反対色応答「モドキ」を見てみたのが次のグラフである。縦軸が「輝度チャンネル」で、向かって左の軸が「青<->黄」チャンネルで、向かって右の軸が「赤<->緑」チャンネルである。この「輝度チャンネル」・「青<->黄」・「赤<->緑」という「感覚的」3次元空間で波長が一方向に変化するスペクトル色を連続的にプロットしてみると、見事に円状につながっていることが判る。「赤<->緑」チャンネルの計算が基本的にはL錐体出力からM錐体出力の差分をとって、さらにS錐体の出力をほんの少しだけ引いてやるという計算をしているため、短波長側でL錐体の感度がM錐体の感度を上回っている(ように実は設定した)のでこんな風になるのだ。単純に波長が短くなるだけなのに、見た感じ何故か紫と赤が近く見える。あくまで、大雑把な話だけれど。
中学の頃の私がこれで納得するとは思えないが、少なくとも今の私はこの円環構造を目にすることができればこれで満足である。
 |
ちなみに、つぎに示すのは輝度が一定になるようにした画像の周辺部をグルッと計算してみたものである。このグラフでは縦軸の「輝度チャンネル」の値はずっと同じで、「青<->黄」チャンネル・「赤<->緑」チャンネル平面内で円環状にグルッと一周しているのがわかると思う。自分自身が下の画像を眺めたときに、つながりが自然だなぁ、あるいは自然じゃないなぁ、と感じる感覚と重ね合わせながら見てみると面白いのではないだろうか。
 |
さて、興味がある方がいらっしゃれば、このバッタもんソフトを使って、ぜひ色々なパラメータを振って色々な画像を読み込んで試行錯誤をしてみてもらいたいと思う。そして、その結果を私に教えていただければとてもうれしい。もちろん、このソフトを使うという話に限らず、面白そうなアイデアがあれば大歓迎である。
さて、虹というとミュージカル「オズの魔法使い」の中でジュディ・ガーランドが歌っていた"OverThe Rainbow"を何故か思い出す。実は、このソフトを作っているときも「ふ〜ん、ふ〜ん、ふ〜んふんふふふ〜ん」と歌詞が判らないまま鼻歌を歌いながら作業していた。歌詞が判らないまま、というのも何なので、せっかくなので調べた歌詞で今回の話を終わらせたいと思う。虹の彼方には…
Somewhere, over the rainbow, skies are blue.And the dreams that you dare to dream really do come true.
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
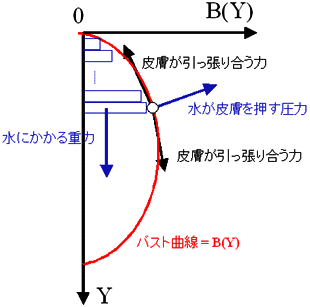
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2002-01-02[n年前へ]
■愛は勝つ 
実家でぼけーっとしながら、私か妹か弟かが買った那州雪絵の「ここはグリーン・ウッド」を眺めていると、懐かしのエピソード「愛は勝つ」を読んだ。
で、「愛は勝つ」の有名?なセリフ「悪は滅びるっていうからな。 … でも、滅びなかったらそれは悪じゃないのかもしれない」というセリフを読んで、「なるほど。それが愛なのかー」と、思ったと同時に「それはちょっと2ちゃんねるに似てるなー」と思ったのだった。「汚かったりキレイだったり、幅広かったり偏狭だったり、それが全部*****なんだー」と思ったわけである。もちろん、*****のところは"愛"でも"2ちゃんねる"でも何でも良くて、人でも科学でも何でも良いのである。
なので、やっぱり"2ちゃんねる"にしても何にしても、それを単純に良いとか悪いとか言えないと私は思うわけで、「悪は滅びるっていうからな。 … でも、滅びなかったらそれは悪じゃないのかもしれない」くらいで…、と書き出そうと思ったけど、あまりにありふれてるのでやめよっと。
2002-02-03[n年前へ]
■映画のフィルムを並べたスクラップ 
映画大好きの「元」少年少女達へ
先日、「お笑いパソコン日誌」で3次元画像ブラウザ「みょう絵」というものを知った。画像ファイルを日付や色の特徴などで三次元空間に並べてみる、というソフトだ。下の図がその「みょう絵」の動作画面だけれど、こんな風に三次元空間に配置された画像が散らばる中を「みゅぃーん」と動く感覚が結構気持ち良い。
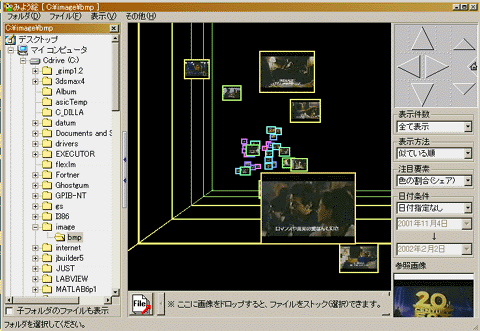 |
で、その「みょう絵」をいじって
欲を言えば画像だけでなくて、色んな文章や音楽や気持ちとか、世の中のありとあらゆるものをこんな風にして眺めてみたいなぁ、と思った。あのころ撮影した写真や、眺めた景色や、読んだWEBサイトや…、とにかくありとあらゆるものを。と思った。すると、「お笑いパソコン日誌」のChic氏が
余談ですが、Windows XP はムービーファイルをサムネイル化してくれるんですが、あらゆるファイルをそうしてくれればいいのにと思ったり。と書いていた。それを読んで、「みょう絵」で一本の映画の中を覗いてみたいなぁ、と思ったのである。
映画が展開していくそのストーリーの時系列と、その中の色々な各舞台を三次元的に眺めてみたいと思ったのだ。そして、さらにはその映画の世界の中を三次元的に散策してみたいと思ったのである。
もちろん、それは映画の動画ファイルを静止画に展開して、それを「みょう絵」で開けばよいだけの話である。以前、動画ファイルを静止画に展開するアプリケーションを作ったこともある。
とはいえ、それを使って映画をキャプチャーしたファイルをそのまま静止画に展開するわけにはいかない。そんなことをしたら、ものスゴイ数の静止画ができてしまうからだ。1秒あたり約30枚もの静止画を含む動画をそのまま静止画に全部落としたら、一体どれだけのファイルができるだろうか?たった2分位の映画の予告編だって、展開したら何と3600枚である…。これだけの画像を読みこませたら、少なくとも私の遅いPCでは「みょう絵」がストライキを起こすことは確実だ。
そこで、映画の動画ファイルの中から、場面が変わるごとに一枚づつ静止画を抽出してみることにした。そうすれば、映画の中の色々な場面をそれぞれ一枚づつの画像として眺めることができる。そして、その画像を集めれば、その映画の色々な場面を一枚のノートにして見ることができるわけである。
というわけで、作ってみたのがこのAVI2Stillsである。いつものように、テキトーに仕立て上げただけだ。下の図がAVI2Stillsの動作画面である。ちなみに、この画面中で、TrigerLebelは場面変化を検出する感度を示すパラメータで、多分60位が適当だと思う。そして、SkipFrameは動画ファイルの中を何フレーム毎に調べていくかを示すパラメータである。展開スピードが気にならなければ1でも構わない。
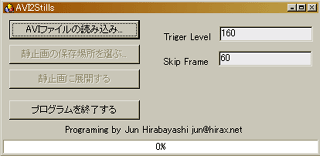 |
このソフトができたところで、試しに - ロケット制作に憧れる少年達を描いた「遠い空の向こうに」"OctoberSky"( = 原作 "Rocket Boys"のアナグラム) - の中の各場面を抽出してみたのが下のスクラップである。予告編の中の各シーンが絵コンテのように抽出され、並べられていることが判ると思う。
 |
こんな風に自分の好きな映画の場面を全部テキトーに抽出して、あとは「みょう絵」で眺めてみれば、その映画の世界を三次元的に散歩できるのである。というわけで、北村薫原作の映画「ターン」の予告編の世界を「みょう絵」で眺めてみたのが下の図である。
 |
静止画では判りにくいけれど、立体的に配置された「映画空間」の中を散策してみるのは、やはりちょっと面白い。これで、欲を言えば各場面に近づくとその場面で流れていた音楽やセリフが聞こえてきたら、面白いと思う。それは、ムソルグスキーの「展覧会の絵」のようで気持ちが良いはずだ。そして、そうすれば気持ちが良いだけではなくて、今の「みょう絵」に足りない「画像だけではない何かをも眺めること」ができるわけだ。
またせっかくだから、「みょう絵」で眺めて終わりにするのも少しもったいないので、以前作った写真アルバム風のスクリーンセーバー"FilmStrip99"(手元のWindows2000では手直しが必要みたいだが…)で、白黒写真のコンタクトフィルム風のスクリーンセーバーを動かしてみた。それが下の画像である。映画のフィルムでなくて、写真のフィルム風だというところはご愛敬で許して欲しい。ちなみに、下の一連の画像は"SomeoneLike You"「恋する遺伝子」の予告編から変換したものである。
こんな風に自分の好きな映画の予告編などを使って自分用のスクリーンセーバーを作ってみるのも面白いと思う。今なら、たくさんの映画の予告編にオンラインでアクセスできるし、その予告編の動画ファイルがもしmov形式ならmov2aviを使って、それがもしrealvideo形式ならTinraを使えば、AVIファイルに変換できる。そして、今回のAVI2Stillsを使えば良いだけなのである。
 |
ところで、こんな切り取った映画のフィルムを繋いだ一連のシーンといえば、ニューシネマパラダイスのラストシーンを思い出す。アルフレードの遺品、「主人公が覗き見ていた一連の場面」を繋いだシーンのフィルム、に主人公が涙したように、かつて少年少女だった映画大好きの人達がそれぞれ自分用のそんなスクラップフィルムを作ってみるのも面白いかも、と思う。そして、ふと思うことがあった時に眺めてみるのも、趣があるかも。
2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
 東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
「福田X小泉っていうのは、結構上手くやっているのかな?」と私が言うと、おもむろに
「あれは、福田X小泉じゃなくて、絶対あれは小泉X福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜?」と私が首を傾げていると、繰り返し
「福田X小泉と小泉X福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か?小泉X福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田X小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか??政治の世界では、言う順番で総理大臣が決まるとでも言うのか?と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ?政界は判るけど、やおい界って一体何処の世界の話だ??と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- X → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物(実際の人物であったり、小説などの登場人物であったり)のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
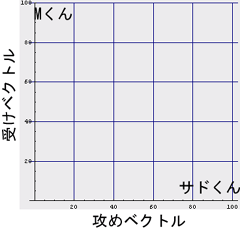 |
そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = (攻め度(s)、受け度(m))と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに(いや別にありがたくはないか…)、この「やおいのカップリング評価演算子」が「福田X小泉」と「小泉X福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか(?)「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか?」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう?... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」