2009-07-18[n年前へ]
■「自分が選ぶであろう道を絶対に反対しないと思われる人」 
小倉千加子「シュレーディンガーの猫―パラドックスを生きる
人は決断に迷うとき、自分が選ぶであろう道を絶対に反対しないと思われる人と物理的に距離を縮めていく。
2010-01-04[n年前へ]
■ナヴィエ・ストークス方程式の誕生秘話
「オッパイ星人の力学 仏の手にも煩悩編::(2001.01.27)」から。
「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
「えっ？おかしいじゃないか、それなら逆に言うと、指も空気からは何の抵抗も受けないってことか？この指先に感じる、まぎれもないおっぱいの感触は幻だとでもいうのか!?」
「これがダランベールのパラドックスだ。」
「そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全ては疑似おっぱいの感触を説明するために、だ。」
2010-09-10[n年前へ]
■「無限」に足しあわされた「有限の世界」
「無限個の数字を足し合わせていった結果（和）が、意外なほどに小さな有限の数になる」ことを不思議だと感じない人は多いと思います。たとえば、A4サイズの紙を半分に折って、その半分をさらに折って、その半分をさらに折って・・・と、無限に折り続けても、その紙片の総和はたかだかA4サイズに過ぎません。「無限の個数を足し合わせても有限の大きさにしかならないこと」も別に不思議ではないし、「有限の大きさのものを切り分けて、無限の個数のものをつくることができる」のも、当たり前田のクラッカーだ、という感じ方です。
そういう人であっても、その「内容」次第で、第一印象でその内容を「自然」と感じるか「不思議」と感じるかは違うのではないでしょうか。たとえば、「アキレスと亀」のパラドクスを不思議だと感じる人もいます。その一方で、「無限個の時間を足し合わせた結果は、無限になることもあれば、有限になることもある。そして、この例の場合には和は有限になる」と自然に思う人であれば、この「アキレスと亀」の話には、特に興味を持たずに終わるかもしれません。
あるいは、「地点Aから地点Bへ移動するためには、まず地点Aと地点Bの中間地点Cに到達しなければならない。さらにCからBへ移動するためには、その中間地点を経なければならない。・・・ということを延々考えてみるならば、地点Aから地点Bまで移動するには無限の点を通過しなければならず、有限の時間で移動することは不可能である」という「内容」を、自然に納得し・あたまをひねってしまう人もいるでしょうし、その一方で、そのロジックを聞いて頭を左右に振る人も多そうです。
もしかしたら、初項a0,公比rの無限等比級数(等比数列の和)は「初項/(1-公比)」なのだから…と、いつでも、どんな問題に対しても常に同じような感覚を持つ人もいるかもしれません。
ところで、こんな問題ならどうでしょう。「手元にボールがあり、このボールは、衝突のたびに運動エネルギーの半分を失います。ためしに、手の高さ、1mの高さから、そのボールを落としてみることにします。すると、そのボールは地面に衝突し、運動エネルギーの半分を失い、50cmの高さまで到達したのちに、また地面にぶつかり（さらに運動エネルギーの半分を失い）・・・ということを考えるとき、そのボールは無限時間運動を続けるか、それとも、有限時間内に停止するか？」という問題です。
先ほどの式で示される有限時間でボールの運動エネルギーは消えてなくなると即答する人もいそうですし、もしかしたら、ボールの運動エネルギーは無限時間後までゼロになるわけがない、だからいつまでもボールは動き続けるに決まっていると断言する人もいそうです。
「無限」「有限」というものほど、感覚を裏切るものはないのかもしれません。私たちの世界はまさに「無限」だとも言えるかもしれませんし、それこそ「有限」だと感じることも多いかもしれません。無限の可能性もあることも真実ですし、それと同時に、その世界には有限の時間しかないことも、これまた事実です。
「無限」のはずの「有限の世界」を目の前にして、あなたはどんなことを考えるでしょうか？「無限」と「有限」とパラドクスを読んで、あなたの連想することは一体どんなことでしょうか。
2013-07-20[n年前へ]
■「誕生日が1〜3月に集中していた戦前日本」では「誕生日のパラドックス」はどうなるか？
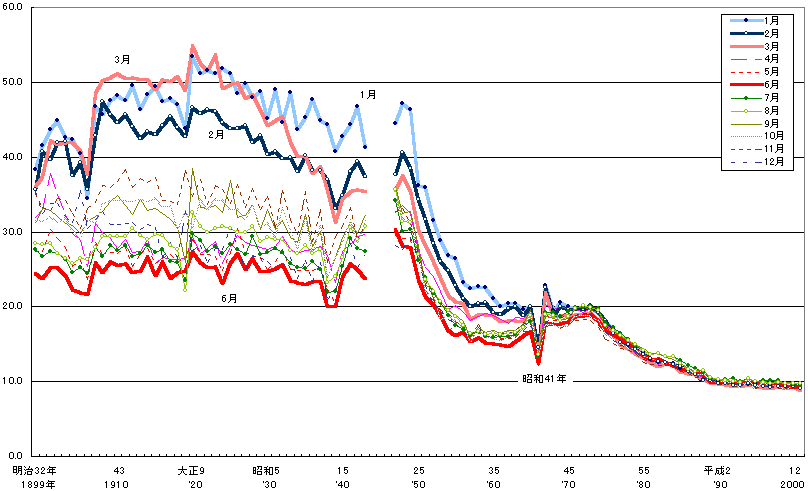「誕生日が1〜3月に集中していた戦前日本」では「誕生日のパラドックス」はどうなるか？
さて問題です。このような誕生日が１〜３月の時期に集中していた戦前の日本で「誕生日のパラドックス」を考えてみると、つまり「何人が集まれば、同じ誕生日の人（たち）がいる確率が50％を超えるか?」を考えてみると、一体どんな答が出てくるでしょうか？…真夏の夜に挑戦するのに丁度良い面白いパズルだと思いませんか？
」など。