2009-09-29[n年前へ]
■IronRuby + Mathematica Player で無料数学演習講座 
昨日に引き続き、IronRuby + Mathematica Player で色んな数式処理をしてみることにします。まずは、昨日のスクリプトのEvaluateToOutputFormの部分を
result=kernelLink.EvaluateToOutputForm(
"NSolve[x^9+x^4+x+5==0,x]", 0)
と変えてみます。つまり、9次の代数方程式を数値的に解いてみよう、というわけです。すると、答えはこんな風に返ってきます。
{{x -> -1.22021}, {x -> -0.859627 - 0.712543 I}, {x -> -0.859627 + 0.712543 I},{x -> -0.277212 - 1.208 I}, {x -> -0.277212 + 1.208 I}, {x -> 0.607409 - 1.01612 I}, {x -> 0.607409 + 1.01612 I}, {x -> 1.13953 - 0.477782 I}, {x -> 1.13953 + 0.477782 I}}9次の代数方程式の解が一瞬で(数値的に)求まってしまいます。
また、
result=kernelLink.EvaluateToOutputForm(
"Simplify[a x + b x +c x -d]", 0)
といった風にすると、"a x + b x +c x -d"を簡約化した答えを返してくれます。たとえば、こんな風です。
-d + (a + b + c) xこの簡約化する作業は間違えてしまうことが多い割に、結構行うことも多い作業だったりするので、Simplifyが使えるのは、とても便利です。
もしも、""Solve[a x^4 + b x^3 +c x^2 -d x + e==0,x]"といったコマンドを投げれば、4次代数方程式の解が帰ってくるわけですが、その解を張り付けるにはこのスペースがあまりに狭すぎるので、貼り付けるのはちょっと止めておくことにしましょう。
あるいは、上の5次方程式で使われている変数に前もって値を代入してやれば、つまり、"a=0;b=0;c=0;d=3;e=1;Solve[a x^4 + b x^3 +c x^2 -d x + e==0,x]"といったコマンドを投げてやれば、
1
{{x -> -}}
3
という風にきちんと答えが返ってきます。
result=kernelLink.EvaluateToOutputForm(
"a=0;b=0;c=0;d=3;e=1;",
0)
result=kernelLink.EvaluateToOutputForm(
"Solve[a x^4 + b x^3 +c x^2 -d x + e==0,x]",
0)
といったように、複数回に分けてコマンドを投げても大丈夫です。自分で苦労して解かなくて済むと、数学の問題も少し楽しく思えます。
 というわけで、Mathematica Playerと.NET/Linkをダウンロードすると、IronRubyなどからMathematicaの機能のかなりの部分を使うことができ、数学の世界を苦労せずに覗いてみることができます。Mathematicaのマニュアルを見ながら、色んな数式処理をさせてみると、きっと面白いと思います。
というわけで、Mathematica Playerと.NET/Linkをダウンロードすると、IronRubyなどからMathematicaの機能のかなりの部分を使うことができ、数学の世界を苦労せずに覗いてみることができます。Mathematicaのマニュアルを見ながら、色んな数式処理をさせてみると、きっと面白いと思います。
2012-04-17[n年前へ]
■百次方程式の係数を複素平面上で動かして、百個の解のダンスを眺め・楽しんでみよう!? 
 多項式からなる代数方程式の「係数」をマウスでつかんで動かした時に、「(その代数方程式の)”解たち”の配置」と「”解たち”が動き回るようす」を眺めたいな…と思ったのですが、ググってみると「x^n + b x + 1 = 0 おいう代数方程式の係数bを複素平面上で動かした時に”解たち”がどのような配置になるか・どのように動き回るか」をインタラクティブに味わえる・楽しむことができる(Monodromy of z^n + b z + 1 = 0)というものがありました。
多項式からなる代数方程式の「係数」をマウスでつかんで動かした時に、「(その代数方程式の)”解たち”の配置」と「”解たち”が動き回るようす」を眺めたいな…と思ったのですが、ググってみると「x^n + b x + 1 = 0 おいう代数方程式の係数bを複素平面上で動かした時に”解たち”がどのような配置になるか・どのように動き回るか」をインタラクティブに味わえる・楽しむことができる(Monodromy of z^n + b z + 1 = 0)というものがありました。
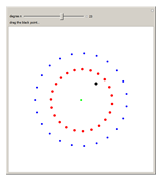
そこで、”x^n + b x + 1 = 0”という二次から百次までの代数方程式で、係数”b”を複素平面上で(マウスで)動かして(青丸)、(その動きに応じて)解の集団(赤丸)が形作る美しいダンスを眺め・楽しんでみました。
中学生くらいの頃、"X^2+2=0"といった方程式を(各々の軸が実数の)XY平面上で黒板の上で眺めつつ、その黒板上に描かれたXY平面には、"Y=X^2+2"というグラフと"Y=0"というグラフが「どこでも交わっていない」ようにしか見えないのに、方程式の「答え」は「(どこかに)2つの解がある」というもので…それは理不尽で不思議で…つまりは納得できなかったような気がします。
 あの頃、複素平面上に複素数値を描いたグラフを見ていたら、黒板の上で多項式の解が複素平面上で円を描いてフォーク・ダンスを踊る風景を眺めていたら…数学に恋をしていたかもしれない、と思います。
あの頃、複素平面上に複素数値を描いたグラフを見ていたら、黒板の上で多項式の解が複素平面上で円を描いてフォーク・ダンスを踊る風景を眺めていたら…数学に恋をしていたかもしれない、と思います。
オクラホマ・ミクサーやマイムマイム…黒板の上の複素平面上で代数方程式の係数が動くにつれ、その方程式の解の群団が踊るフォークダンス…が今日見た景色、です。