2009-07-21[n年前へ]
■50%のうまくいく可能性を四捨五入しちゃえば… 
 加納朋子の「ななつのこ (創元推理文庫)
加納朋子の「ななつのこ (創元推理文庫)
」から。
結局、世の中なんて、うまくいくか、いかないかのどっちかよ。まあ統計学的にみて、五十パーセントはうまくいくわけですよね。四捨五入しちゃえば、十割だわ。
2009-11-04[n年前へ]
■きみが見つける物語 
「京都市鴨川源流」を廻る「理系風デート」で紹介した何人かの作家による小話を集めた短編集である「きみが見つける物語 十代のための新名作 休日編 (角川文庫 あ 100-103)
」はシリーズになっていて何冊か出ています。、5人の作家、この「休日編」では、角田光代・恒川光太郎・万城目学・森絵都・米澤穂信という人たちが書いています。どの作家が描く世界も、切なさ・やるせなさ・楽しさ・・・あるいはたくさんの感情を与えてくれる素晴らしいものばかりです。
 シリーズの一冊、「きみが見つける物語 十代のための新名作 スクール編 (角川文庫)
シリーズの一冊、「きみが見つける物語 十代のための新名作 スクール編 (角川文庫)
」では、あさのあつこ・恩田陸・加納朋子・北村薫・豊島ミホ・はやみねかおる・村上春樹というこれまた魅力的な作家たちの作品がまとめられています。先の「休日編」と同様に 藤田香織氏による紹介・解説と・各作家の作品が収められています。
「スクール」を舞台にした作品はどれも、自由さとよく自由の狭間で、はっきりとは見えない可能性の中を生きていく(生きてきた)主人公たちが描かれています。豊島ミホの「タンポポのわたげみたいだね」で始まり、村上春樹の「沈黙」を最後に置かれることで、全く別々の作家の別の作品なのに、まるで、一つのテーマを扱った短編集のようになっています。
「まだ時間は早いけれど、ビールでも飲みませんか」と少しあとで彼は言った。飲みましょう、と僕は言った。たしかにビールが飲みたいような気分だった。
村上春樹 「沈黙」
「休日編」「スクール編」ともに文庫本ですが、小さい割に、とても密度の高い本です。カバンに入れておくには、とても良い本だと思います。
2010-04-12[n年前へ]
■拡散方程式で考える「あみだくじ空間」と「空間ワープ」 
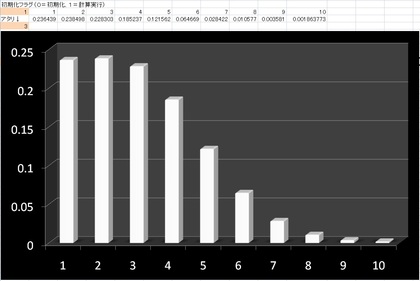 「あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる」で、あみだくじの(平均的な)動き方を1次元の拡散方程式で解き、アタリを引く確率分布を考えてみました。
「あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる」で、あみだくじの(平均的な)動き方を1次元の拡散方程式で解き、アタリを引く確率分布を考えてみました。
そのことに関して会話をしている中で、「とても新鮮で、着想が面白いな」と感じることがありました。そのアウトラインはいずれ平易な形で紹介させて頂くこととして、ここでは、マニアックで一般受けしそうにない部分を、マニアックで一般受けしそうにない記述で、そのとても面白かった話題を書いてみようと思います。
といっても、hirax.netを読みに来る人は、これすなわち、一般的ではないとってもニッチ(≠リッチ)な変わりものであるわけですから、そういった方には、ちょっと面白いのではないか・楽しめるのではないか、と思います。
前回紹介したように、あみだくじのアタリの場所がわかっている時には、その(平均的な)動き方を1次元の拡散方程式で解くことで、(平均的には)ここがアタリやすい場所だ、ということを求めることができます。アタリの場所が中央でなく、横線が十分にたくさんある場合には、アタリが左に寄っているなら左端、アタリが右に寄っているなら、右端がアタリやすい場所になります。横線の数が少なく、アタリが端にそれほど近くない場合には、アタリの真上がアタリの確率が高くなります。
 端っこが確率が高くなるのは、両端がノイマン条件になっていて、両端で折り返される部分多重に重なるから、ということになります。部屋の中のゴミの動きをランダム・ウォークで考えたとき、四隅にゴミが滞留しやすいのと同じ具合です。
端っこが確率が高くなるのは、両端がノイマン条件になっていて、両端で折り返される部分多重に重なるから、ということになります。部屋の中のゴミの動きをランダム・ウォークで考えたとき、四隅にゴミが滞留しやすいのと同じ具合です。
そんな話をしているとき、「じゃぁ、こんな線を引いたら?」「あるいは、こんなのは?」と言いながら、下図のような2つのケースのあみだくじ(の横線)を引かれました。…これは、ちょっと、とても面白い新鮮で面白い着想だと思いませんか? 確かに、そういう線を、私たちはよく引きます。けれど、そういうことを、年を経るうちに、いつの間にか忘れてしまっていたことに気づかされました。
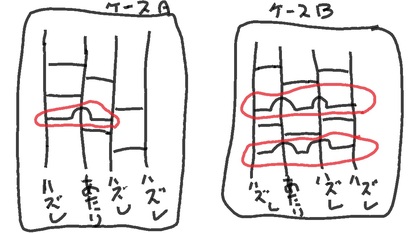
ちなみに、上図のケースAのような場合、あみだくじを表現した1次元の拡散方程式で言うと、拡散の速さが速くなることになります。短い時間(あみだくじで言うなら、縦方向の距離で)で、アタリの場所が遠くまで移動していくことになります。つまり、遠くと遠くの空間を結び付ける、これは一種の”ワープ”する線です。
そして、上図 ケースBの場合には、左右の両端が、「ノイマン条件」でなく、「周期境界条件」に(線の数がある分だけ)変化していきます。この場合も、結局は、一種の”ワープ”する線であって、それが空間の「反対側」どうしを結び付けている、という具合です。
結局、これらの”縦線をまたぐ”ような線は、離れた場所を強引に結びつけ、その空間どうしを”ワープ”できるようにすることで、隣り合った空間にさせてしまう、という恐ろしい効果をもっていることを、その当たり前のことを、空間内の拡散現象を表現する拡散方程式を解く、ということをする中で眺めると、ことさらに強く印象付けられます。
拡散方程式で考える「あみだくじ空間」と「空間ワープ」…何だか、そんなことを考え始めると、ルイス・キャロルの「不思議の国のアリス
」のように、不思議で魅力的な迷路のような空間中を探検しているようで、とても面白い心地になりませんか?
この話題、もう少し、続きます。
だってそうでしょう?箱は開けてみなきゃ、中身はわからない。電話は出てみなきゃ、相手はわからない… 少なくとも、旧式の電話はね。
人の心だってそうよ。…こうして…ノックしてみないと、わからないの。
加納朋子「螺旋階段のアリス」
2010-11-24[n年前へ]
■50パーセントは…四捨五入しちゃえば10割だ 
加納朋子「ななつのこ
」から。
「結局、世の中なんて、うまくいくか、いかないかのどっちかよ。まあ統計学的にみて、五十パーセントはうまくいくわけですよね。四捨五入しちゃえば、十割だわ」
2011-10-20[n年前へ]
■「銀色チューブ」には「油で練り込んだ化学式」が詰まってる 
 短編連作小説集である、加納朋子の「掌の中の小鳥
短編連作小説集である、加納朋子の「掌の中の小鳥
」の冒頭「掌の中の小鳥」の前半に書かれている、雲雀(ヒバリ)の油絵に関するエピソードから。
あのとき君が描き出した色は、本当にきれいだったね。曖昧で、微妙な色彩だった。今まで見たどんな絵にも、あんな色はなかった。だけど、それも当然だった。君は絶対に混ぜ合わせちゃいけないとされる色ばかり選んで、あの絵を描いたんだ。
ウルトラ・マリーン(ケイ酸アルミナ・ナトリウム)とエメラルド・グリーン(酢酸亜ヒ酸銅)、クローム・グリーン(クローム酸鉛とフェロシアン化第二鉄)とカドミウム・イエロー(硫化カドミウム)なんて具合にね。
僕は考えたこともなかったよ。あの銀色のチューブの中身が、化学式を油で練り込んだものだなんてね。