1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
 | 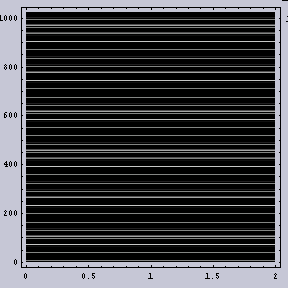 |
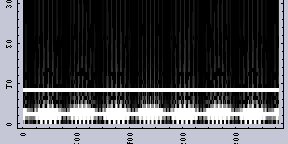
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
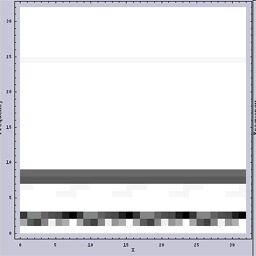 |  |
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
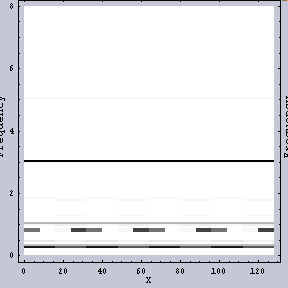 | 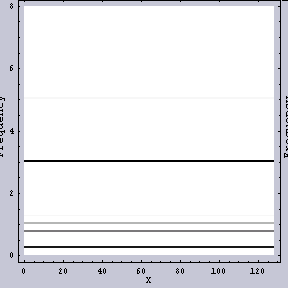 |
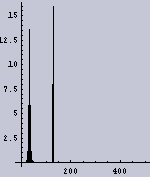
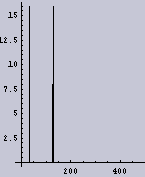
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
 |  |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
1999-01-03[n年前へ]
■オシロスコープソフトを作る 
PCを2Ch高性能オシロスコープにしたい
オシロスコープがあると便利だが、家で使うには敷居が高いし、値段も高い。まして、FFTアナライザーがついて周波数解析も行うことができるような機械になると、遊びで買うという値段ではなくなってしまう。そこで、PCを2Ch高性能オシロスコープにするソフトを作ってみたい。
以前、音階を調べた時に、SoundBlaster互換I/Fを使ったLabViewのサウンド入出力のViを使用してみる。目標はとにかくオシロスコープと同じ使い勝手であること、使うのが簡単であること、そして、周波数解析などが簡単に行うことができること、である。入力として、音声入力を使用しているので、たいていのPCで使うことができるし、音声入力マイクが着いているPC(たいていのノートPCは着いているだろう)なら、マイク(あるいは入力端子)を用意する必要すらない。
というわけで、下がそのアプリケーションの画面。
 |
20KHz(ナイキスト周波数で言えば正確には10KHzか)までしか、使うことはできないが、ちょっと使いたい時には便利だ。特に、音声を解析したいならば、必要十分である。上の画面では口笛を吹いて、その音声波形を表示させ、周波数解析を同時に行っている。周波数ピークが表示され、1120Hzであるという表示がされる。
内蔵マイクを使用すると、ただアプリケーションを走らせれば、音声周波数解析が行える。もしも、比較的高性能なマイクがPCに着いているならば、リアルタイム振動解析すら行うことができる。もちろん、マイク入力端子に何らかの入力をすれば、どんな解析もできるわけだが、何の用意もせずにできるというのは便利である。例えば、うるさいデスクトップPCの近くへこのアプリケーションを走らせたノートPCを近づけると、デスクトップPCがなぜうるさいかを簡単に調べることができる。うるさいのは、ハードディスクの周波数なのか、ファンの周波数なのかすぐにわかる。
今回、作成したアプリケーションはここにおいておく。動作させたら、レンジを調整することを忘れずに。
Ocilo.lzh LZH形式 1,259kB (打ち止めです。あしからず。)
LabViewのアプリケーションライセンス上、ダウンロード数は50回までで、その数近くになったら削除することにする。
1999-02-27[n年前へ]
■画像ノイズ解析について考える 
考える理由
画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。その疑問とは次のようなことである。
- 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
- 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
- また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。
2D-FTと2D-Waveletの例
はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。 |  |  |
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。
それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか?
 |  |
| 高周波のX成分 | 高周波成分 |
| 低周波成分 | 高周波のY成分 |

もう何分割かしてみる

なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。
 |
ドットのノイズを解析してみる
それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。 |  |
 |  |
右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。
 |  |
 |  |
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
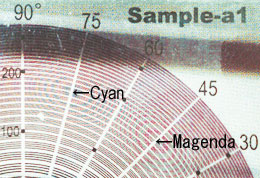
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2004-02-14[n年前へ]
■アダルトビデオの科学 今日のトリビア 編 
「帰ってきたオッパイ星人の力学 アダルトビデオ鑑賞 編(仮題)」改め、「アダルトビデオの科学 今日のトリビア編 - 横揺れ縦揺れ2.5ヘルツ -」です。
アダルトビデオの振動方向はジャンルによって違うが、一秒間に2.5往復ほどである。ブロックマッチング、モルレーのウェーブレットで時系列周波数解析、そんなこんなでエロエロを解析。えっ、こんなテクノロジーを使っても解析する対象を間違えているんでしょうか?しかし、そんな科学や新しいテクノロジーを牽引している原動力も(時には)エロエロだったりするわけです。
気づけば今年初の「できるかな?」、しかも聖バレンタインな日にこともあろうに「アダルトビデオの科学」 うぅ。それでも…「それもまた良し」ということにしておきましょうか。
