2008-06-13[n年前へ]
■「爆乳でなくなったら歩けない」を科学する 
 「爆乳」という言葉の名付け親と「メガ乳」という言葉の名付け親と話をした時に、「新鮮に聞こえるが普遍的にも聞こえる」話を聞き、面白さを感じた。そんなことを感じた話のひとつが、こんなことである。
「爆乳」という言葉の名付け親と「メガ乳」という言葉の名付け親と話をした時に、「新鮮に聞こえるが普遍的にも聞こえる」話を聞き、面白さを感じた。そんなことを感じた話のひとつが、こんなことである。
(IとかKカップとかいった爆乳の女優さんの多くが言うことには)「バストが小さくなったら、歩き方がわからない」「もう歩けなくなってしまうかもしれない」
2kgほどの重量物を胸部に二つも可動する状態で歩こうとしたなら、「重量物の揺れ・振動」を抑えつつ、それでも抑えきれない重量物の揺れと共存した歩き方にならざるをえないはずだ。つまりは、大きなバストがあること前提の歩き方になっているに違いない。だから、「バストが小さくなったら、歩き方がわからなくない」ということになるのだろう。
ところで、可動する重量物、端的に言えば・揺れるバストは、下に描いたようなバネ・ダンパモデルとして単純にモデル化することができるだろう。つまり、その図の下に書いた微分方程式で表されるダイナミック・システムである。あるいは、それを伝達関数モデルにまでしてしまえば、つまりはさらに下に描いた「2次遅れ要素」である
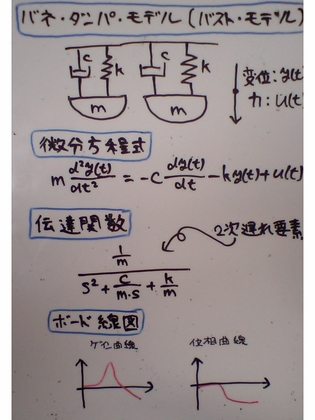
電気のRLC回路(発振回路)なども、上の微分方程式と同タイプの式で表現される。そして、発振回路でコンデンサの容量(C)がいきなり小さくなってしまった場合などは、当然ながら発振周波数も変わり、その結果、回路の動きは大きく姿を変えることになる。つまり、「容量が小さくなってしまったら、(それまでの動かし方では)回路が動かなくなってしまう」という状態になるわけだ。
つまり、上に描いた「メガ(爆)乳」を表現したダイナミック・システムと電気回路の間には、類似性(アナロジー)があって、それらは共通の普遍性を垣間見せるわけである。
 だから、実は、電気工学や機械工学のエンジニアたちこそが「爆乳の女性人たちが経験的に会得した歩き方の工夫」の一番の理解者になったりするかもしれない、と思ったりもするのである。「そうそう部品の定数がいきなり変わったら困っちゃうよね」と大いに共感できそうなきもするのだ。……もちろん、そんな妄想に「そんなわけない」とすぐに突っ込みたくもなるのだが。
だから、実は、電気工学や機械工学のエンジニアたちこそが「爆乳の女性人たちが経験的に会得した歩き方の工夫」の一番の理解者になったりするかもしれない、と思ったりもするのである。「そうそう部品の定数がいきなり変わったら困っちゃうよね」と大いに共感できそうなきもするのだ。……もちろん、そんな妄想に「そんなわけない」とすぐに突っ込みたくもなるのだが。
2008-07-26[n年前へ]
■Simulinkで”日焼け対策”を最適化 Vol.1 [はじめに 編] 
 先日、Mathematicaで肌の色や日光の色スペクトルを表現するためのライブラリを作り、いくつか計算をしてみました。また、昨日は、「日焼けに影響を与える日照時間」の変化・「気温の変化」「化粧品の商品切り替え時期」「日焼け対策を行う時期」について考えてみました。
先日、Mathematicaで肌の色や日光の色スペクトルを表現するためのライブラリを作り、いくつか計算をしてみました。また、昨日は、「日焼けに影響を与える日照時間」の変化・「気温の変化」「化粧品の商品切り替え時期」「日焼け対策を行う時期」について考えてみました。
そんなことを考え出すと、究極の”日焼け対策”・至高の”日焼け対策”はどういう風にすれば良いだろうか、という技術的な興味が湧いてきます。もちろん、外に一切出ない・顔には紫外線反射膜をコーティングする、といったような対策もあるわけですが、そんな対策をしても「そんな毎日でいいのか?」という疑問を感じるに違いありません。やはり、色々な観点を含めた上で、それらの観点を少しづつ満たすような”日焼け対策の最適化”を考えなければならないように思われます。
そこで、Simulinkを使って、(動的なシステムのモデル化・制御システム構築・プロトタイピングを簡単に行うことができる)MATLAB社のSimulinkで”日焼け対策”を最適化に挑戦してみたくなりました。そこで、今日はまず[はじめに]ということで、平均日照時間と平均気温をSimulinkでグラフ表示してみました。
とりあえず、下の微分方程式のように平均気温(TEMP)の変化は平均日照時間(SUN)に比例するとおくと、
d TEMP /dt = SUN平均気温は平均日照時間を積分したもの、ということになります。そんな関係をSimulinkでモデル化し(数値はまだ合わせていません)、グラフ表示してみたのが下の図です。気温が日照時間に対する「位相遅れ」を持っていることがわかります。
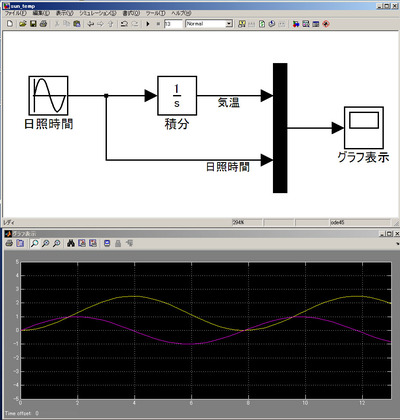
・・・と、ここまでは当たり前の結果ですが、こんな感じで「日焼け対策の最適制御」について色々考えていこうと思います。
2009-12-16[n年前へ]
■エクセルでシミュレーション Vol.10 二次元非定常熱伝導問題シミュレーション+P(ID)制御エクセルシートを作ってみよう 
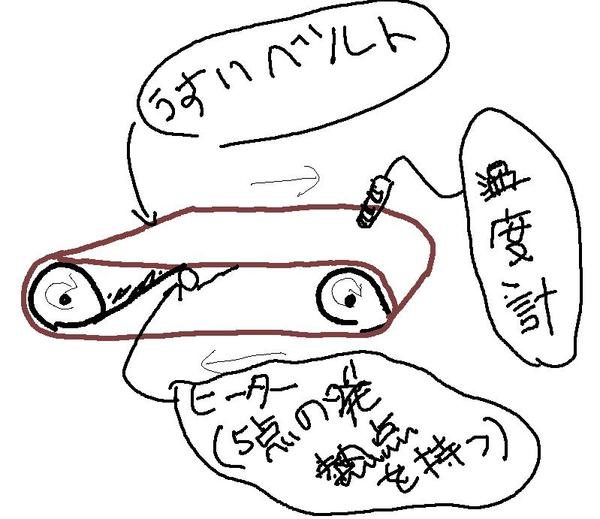 「エクセルでシミュレーション Vol.9 二次元非定常熱伝導問題の温度変化グラフも作ってみよう」で、二次元非定常熱伝導問題を解くシートを使いながら(実用的範囲では三次元問題と大差がない)、ヒーターで回転するベルトを高温にした場合の、その回転ベルトの温度分布がどのように変化していくかを計算し、グラフ化し、さらにベルト中の一部分の温度を時系列的にモニターする機能を付けた、シートで遊んでみました。
「エクセルでシミュレーション Vol.9 二次元非定常熱伝導問題の温度変化グラフも作ってみよう」で、二次元非定常熱伝導問題を解くシートを使いながら(実用的範囲では三次元問題と大差がない)、ヒーターで回転するベルトを高温にした場合の、その回転ベルトの温度分布がどのように変化していくかを計算し、グラフ化し、さらにベルト中の一部分の温度を時系列的にモニターする機能を付けた、シートで遊んでみました。
そこで、今回は、センシングしたベルトの温度を用いて、ヒーターの温度を簡単なPID制御を使ってフィードバック制御するエクセル・シートを作ってみることにしましょう。
PID制御とは、調整量を(現在の)出力値と目標値との差に比例=Proportionalした量、その(過去からの)積分=Integralに応じた量、および(その瞬間に次にどのように変化するかという)微分=Differentialに応じた量にしたがって変える制御です。言いかえれば、現在(Proportional)・過去(Integral)・未来(Differential)の挙動に応じて、制御調整量を変えてやろうという制御です。比較的、古典的な制御手法ですが、現在でも、もっとも一般的な制御手法です。
 まずは、前回のエクセル・シートでヒーター部分を単純に(計算をさせ始めてから=回転ベルトに対するヒーターを動かし始めてから)100℃にし続けた場合の計算過程を示してみます。つまり、何の制御もしない場合です。その計算結果が、下の動画です。上の動画で上に示したグラフが、回転ベルトの温度分布を示したグラフです(回転ベルトを切り開いたように温度分布を示しています)。動画中の下の折れ線グラフは(上のコンター図で灰色丸部の温度の時間変化を示したグラフです)。ちなみに、縦軸は0℃から150℃までで、横軸が時間軸です。
まずは、前回のエクセル・シートでヒーター部分を単純に(計算をさせ始めてから=回転ベルトに対するヒーターを動かし始めてから)100℃にし続けた場合の計算過程を示してみます。つまり、何の制御もしない場合です。その計算結果が、下の動画です。上の動画で上に示したグラフが、回転ベルトの温度分布を示したグラフです(回転ベルトを切り開いたように温度分布を示しています)。動画中の下の折れ線グラフは(上のコンター図で灰色丸部の温度の時間変化を示したグラフです)。ちなみに、縦軸は0℃から150℃までで、横軸が時間軸です。
下の折れ線グラフを見れば、上のコンター図で灰色丸で示した部分の、温度が時間に応じて上昇し、やがて100℃近くになっていることがわかります。
 さて、次にPID制御を行ってみることにしましょう。…とはいえ、最初は簡単のために、「灰色丸で示した部分の温度と目標調整温度である100℃との差をヒーターに足す(ネガティブ・日―ドばっく)」という「P=比例成分=現在の違い」だけを利用したP(ID)制御を行ってみます。つまり、現在の出力と目標出力の差異のみをヒーター出力に(適当な比率で)足し合わせてみるのです。言いかえれば、ベルトの温度が0℃なら、ヒーターを200℃くらいにすることで、急激にベルトを温め温度を調整し、目標温度100度と現在のベルト温度の差が小さくなってきたら、ヒーターの温度を110℃くらいに変えてやる・・・というような制御をしてみます。そんなシミュレーション計算を行ってみた結果が、下の計算結果になります。ちなみに、ヒーターの制御温度はエクセルのシートでB32セルで計算されています。また、灰色丸のセンサ取り付け部分(を示した)の温度を示す下の折れ線グラフは、先ほどと同じく、縦軸は0℃から150℃までの温度を示し、横軸が時間軸となっています。
さて、次にPID制御を行ってみることにしましょう。…とはいえ、最初は簡単のために、「灰色丸で示した部分の温度と目標調整温度である100℃との差をヒーターに足す(ネガティブ・日―ドばっく)」という「P=比例成分=現在の違い」だけを利用したP(ID)制御を行ってみます。つまり、現在の出力と目標出力の差異のみをヒーター出力に(適当な比率で)足し合わせてみるのです。言いかえれば、ベルトの温度が0℃なら、ヒーターを200℃くらいにすることで、急激にベルトを温め温度を調整し、目標温度100度と現在のベルト温度の差が小さくなってきたら、ヒーターの温度を110℃くらいに変えてやる・・・というような制御をしてみます。そんなシミュレーション計算を行ってみた結果が、下の計算結果になります。ちなみに、ヒーターの制御温度はエクセルのシートでB32セルで計算されています。また、灰色丸のセンサ取り付け部分(を示した)の温度を示す下の折れ線グラフは、先ほどと同じく、縦軸は0℃から150℃までの温度を示し、横軸が時間軸となっています。
この結果動画を見るとわかるように、「P=比例成分=現在の違い」だけを利用したP(ID)制御(=積分成分と微分成分を使わない)制御では、ベルトの温度は早く立ち上がりますが、ベルトの温度は振動して、なかなかすぐに安定してくれません。しかも、早く温度を立ち上げようとすると、温度振動は大きくなってしまい、温度振動を防ごうとすると、なかなか温度が早く立ち上がってくれない、という相反する関係になっています。いわば、(ある程度、減衰がある)強いバネと弱いバネの振動と同じような現象が起きてしまいます。
 さて、それでは、一体どうしたら良い制御ができるのでしょうか。・・・せっかく、簡易にエクセルのような(表計算=スプレッドシート・ソフトウェアを使った)熱伝導方程式を使ったシミュレーション計算を行うことができる環境があるわけですから、今回扱ったPID制御のような古典的な制御をもう少し復習してみようと思います。
さて、それでは、一体どうしたら良い制御ができるのでしょうか。・・・せっかく、簡易にエクセルのような(表計算=スプレッドシート・ソフトウェアを使った)熱伝導方程式を使ったシミュレーション計算を行うことができる環境があるわけですから、今回扱ったPID制御のような古典的な制御をもう少し復習してみようと思います。
そして、せっかく熱伝導方程式を計算してみたりしているわけですから、そういった微分方程式(つまり現在から未来を示す式)を使うことで実現できる、最適化制御についても考えてみることにします。
2010-08-23[n年前へ]
■離散化した「微分方程式」を描いて遊ぶのにお勧めなプログラミング言語は何でしょうか? 
 ふと思い立ち、とある技術雑文を書き始めました。内容は、適当な物理現象のふるまいを数式で記述して、その動きを把握すると同時に・その物理現象をどのように制御したら良いのかを考えてみよう、というものです。
ふと思い立ち、とある技術雑文を書き始めました。内容は、適当な物理現象のふるまいを数式で記述して、その動きを把握すると同時に・その物理現象をどのように制御したら良いのかを考えてみよう、というものです。
物理現象のふるまいを記述し・解析してみようとする時、とりあえず簡単な方法として「微分方程式モドキを書き、その動きを眺めてみる」というものがあります。「一瞬のふるまいを記述する」ような微分方程式や、差分方程式や、あるいは、漸化式のようなものをまずはラフスケッチのように描いてみて、あとは、初期条件を決めることで「すべての瞬間のふるまい」を追いかける、というようなやり方です。そして、その動きを眺めてみるわけです。
 …すると、そんな作業は、数列(というかベクトル列)を再帰的に解かせる記述をする作業になることも多いように思います。そんなとき、実際に計算もさせつつ、そんな記述を行うときには、一体どんなプログラミング言語が良いのだろう?とふと考えました。…なぜかというと、再帰的な定義式を書いたあとに、計算速度向上やオーバーフローを防ぐために、いつもそのコードをループ文で書き直す作業をしていることにようやく気付いたからです。…こんな作業は(自分でやらずとも)自動的に行ってくれる処理系は絶対あるはずだ、ということにようやく今更ながらに気付いたのです。
…すると、そんな作業は、数列(というかベクトル列)を再帰的に解かせる記述をする作業になることも多いように思います。そんなとき、実際に計算もさせつつ、そんな記述を行うときには、一体どんなプログラミング言語が良いのだろう?とふと考えました。…なぜかというと、再帰的な定義式を書いたあとに、計算速度向上やオーバーフローを防ぐために、いつもそのコードをループ文で書き直す作業をしていることにようやく気付いたからです。…こんな作業は(自分でやらずとも)自動的に行ってくれる処理系は絶対あるはずだ、ということにようやく今更ながらに気付いたのです。
 再帰的なコードを書いたら、あとはそれをループ処理に変え最適化を行ってくれる「いわゆる末尾最適化」をしてくれるプログラミング言語にはどんなものがあるのでしょう?Scheme、Haskell…それともそれ以外の何かでしょうか。離散化した「微分方程式」で遊ぶのにお勧めのプログラミング言語は何でしょうか?
再帰的なコードを書いたら、あとはそれをループ処理に変え最適化を行ってくれる「いわゆる末尾最適化」をしてくれるプログラミング言語にはどんなものがあるのでしょう?Scheme、Haskell…それともそれ以外の何かでしょうか。離散化した「微分方程式」で遊ぶのにお勧めのプログラミング言語は何でしょうか?
2012-05-29[n年前へ]
■ニュートンも解けなかった「しょんべん小僧のションベンの軌跡」 
 「ドイツで16歳の少年、ニュートンも解けなかった難問の答えを見つける」という記事を読みました。関連記事を読んでみると、次のような形に書き下すことができる、「速度に比例する抵抗を受けながら、空気中を飛翔する物体の軌跡」を解いた、ということのようです。
「ドイツで16歳の少年、ニュートンも解けなかった難問の答えを見つける」という記事を読みました。関連記事を読んでみると、次のような形に書き下すことができる、「速度に比例する抵抗を受けながら、空気中を飛翔する物体の軌跡」を解いた、ということのようです。
x''[t] = -a * x'[t] * sqrt( x'[t]^2 + y'[t]2 )
y'' [t]= -a * y'[t] * sqrt( x'[t]^2 + y'[t]2 ) - g
ニュートンも解けなかったという「この問題」、これはまさに『風上に向かう「しょんべん小僧」』で扱った問題です。
今からちょうど10年前、「しょうべん小僧」の解析をした時には(今回明らかになった解析解がありませんでしたから)数値解析をもとに記事を書いたわけですが、そんな「しょんべん小僧のションベンの軌跡」に関する解析解を、ドイツ在住16歳の少年が明らかにした、というわけです。
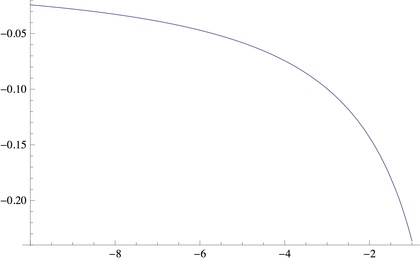 そんなこんなで(16歳の少年が見つけた)「ニュートンも解けなかった難問の答」…つまりは、ニュートンも解けなかった「しょんべん小僧のションベンの軌跡」を(彼が見つけた解析解を用いて)図示してみたのが右の画像です。
そんなこんなで(16歳の少年が見つけた)「ニュートンも解けなかった難問の答」…つまりは、ニュートンも解けなかった「しょんべん小僧のションベンの軌跡」を(彼が見つけた解析解を用いて)図示してみたのが右の画像です。
ドイツ在住の16歳の少年が見つけ出した解析解、…強風の中で「立ちション」せざるをえない状況に立たされた男性たちは、この解析解を読み解き・最適な立ちションスタイルを見つけ出すと、大惨事にならずに済むのかもしれません!?
(なお、グラフ描画に用いた数式は下に貼り付けたものになります)