hirax.net::Keywords::「放熱」のブログ

■ゴールデンボールズの放熱問題を解いてみる!?　

　中国語の金玉と日本語の金玉と全然意味が違うという話をしていると（「金玉満堂」と「福来る」）、「日本語の方の語源は何に遡るのか？」「日本語の方が指し示すものの”しわ”は放熱のためか？」という全く別の２つの話題となった。「”しわ”は放熱のためにある」ということの真偽はわからないけれど、もしもその放熱効果を考えてみるならば、”しわ”があることによって、一体どのように効率的な冷却が行われるものだろう？

　放熱・冷却の効果は、皮膚の表面における"各領域での(皮膚と空気層の)温度差"を表面積にわたって積分したものに比例しそうに思える。また、皮膚内部における伝熱も重要であるに違いない。大雑把にラクガキしてみれば、それは下の図の「緑色の面積が大きいほど放熱・冷却効果が大きい」というイメージになる。

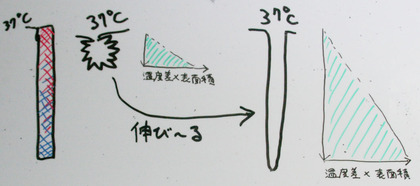
　皮膚の”しわ”の効果、表面積の増加、”しわ”が伸びることによる”皮膚と空気層の温度差"の増加、あるいは、（体の）本体と離れることによる伝熱の違い……などを考えていくと、答えを解析的に解くのは困難であるように思える。

　暑い夏になった頃、夏休みの宿題がわりに"エクセルで金玉の放熱問題を数値的に解いてみる"ことにしよう。暑さを吹き飛ばす放熱問題を解いてみることにしよう。

■「汗のかきやすさは体重のルートに比例する」という「汗っかきの方程式」　

　太っている人は暑がりで、痩せている人は寒がりなのが普通です。単純に考えてみれば、人が発生する熱量は、おおよそ体重に比例するのに対し、体からの放熱は体表面積に比例するからです。太っている人、言い換えれば「体重（発熱量）の割に表面積（放熱量）が小さい、まるで球のような体型の人」はアッチッチになりやすいでしょうし、「体重（発熱量）の割に表面積（放熱量）が大きい、痩せぎす体型の人」ならあっという間に熱を奪われブルブル震えてしまうに違いない、というわけです。

　今日は「体重が増えると何倍暑がりになりやすいか」を考えてみようと思います。藤本らによる「実測値に基づいた日本人の体表面積の算出式」は次のようになります。

体表面積(cm^2) = 88.83 * 身長(cm)^0.663 * 体重(kg)^0.444

　体重を（上の式で求めることができる）対表面積で割ることで「体重（＝発熱量）/体表面積（＝放熱量）」つまり「放熱能力あたりの発熱量＝アッチッチになりやすさ（≒汗のかきやすさ）」を計算する式を作り出すことができます。それが次の「汗っかきの方程式」です。

汗のかきやすさ= 0.0112575 体重(kg)^0.556 / 身長(cM)^0.663

同じ体重なら、体重の約0.5乗、すなわち「体重のルート」に比例して汗をかきやすくなるのです。体重がもし２倍になれば、ルート２＝約1.4倍汗っかきになるのです。あるいは、もしも同じ体重なら、身長の0.7乗、これも（大雑把に言ってしまえば）「身長のルート」に比例して寒がりになる、とも言えるわけです。

　「体重が何倍になれば（横軸）何倍汗っかきになるか（縦軸）」を描いてみたのが右のグラフです。つまりは、「汗のかきやすさは体重のルートに比例する」という「汗っかきの方程式」を単純な場合で眺めた結果例になります。

　季節が変わり、冬の寒さを感じるようになりました。「寒さ」をふと感じたときには、「汗っかきの方程式」を頭に思い浮かべてみるのも面白いかもしれません。

■「自転車を漕ぐ」と涼しくなる？それとも暑くなる!?　

　真夏日が続くと、体にまとわりつく暑さを吹き飛ばしすやり方を知りたくなります。そこで「うちわの効果を検証 体温は涼風で低下か、それともあおぐ労力で上昇か」という記事を読みました。

　暑い日にうちわで風を送ることに意味はあるのか。結局、あおぐことで体温が上昇するだけではないのか。

　…人間が生産するエネルギーは約100ワットだ。うちわをあおげば、約１ワットがこれに加わるかもしれないが、体の周辺の空気の速度が大幅に増すことで、ヒートロスは倍増し得る。1％の努力で、2倍の涼しさを得られる可能性があるのだ。

「うちわの効果を検証 体温は涼風で低下か、それともあおぐ労力で上昇か」

　皮膚の周りの空気が（汗が蒸発できるくらい）湿度が低かったり、あるいは、体温よりも温度が低ければ、ほんの少しの風が吹くだけで少し心地良く涼しくなることってあるよなぁと思いつつ、（真夏日に自転車を漕ぎながら）「自転車を漕ぐ」と涼しくなるか？それとも暑くなるか…というパズルを考えたくなりました。

　自転車を漕ぎ始めると、体に風が吹き付けてきて、そして涼しくなります。ほんの少し速度を上げると、体を冷やす風速も増して、もっと涼しくなります。

　それでは、さらに自転車を速く漕いでいけば、もっともっと涼しくなるものでしょうか？…残念ながら、そういうわけにはいきそうにありません。

　自転車を漕ぐとき、速度が遅くないのなら、自転車を漕ぐエネルギーはほとんど空気抵抗に抗（あらが）うために使われます。自転車で走る速度（と体のサイズ）を考えると、レイノルズ数は十分に大きく体の周りには乱流が発生し・空気抵抗係数は一定になります。その結果、空気抵抗は速度の２乗に比例します。（レイノルズ数が小さければ、空気抵抗係数は速度に反比例するため、空気抵抗は速度の１乗に比例します）

　空気抵抗が速度の２乗に比例するということは、空気抵抗を受けながら自転車を漕ぐのに使われる仕事率（時間あたりに使われるエネルギー）は速度の３乗に比例することになります。つまり、自転車を走らせる速度の３乗に比例する「熱」が（自転車を漕ぐ）体の中で発生することになります。

　次は、その熱を発する体を冷やす「放熱」について考えてみます。汗の影響を考えない場合、そして体温より気温が低い場合、体から周りの空気への放熱量は体温と気温の温度差に比例します。その比例係数は、速度（レイノルズ数）のn乗に比例する関数になりますが、nは大きくても1未満です（体と接することができる空気は、乱流が発生しないという最大限の場合でも、速度の１乗に比例しますから）。つまり、放熱量は速度の0.△乗に比例する程度の量になります。

　汗の影響、つまり汗が気化することで皮膚から奪う熱量も、その熱量の上限は（湿度が高くて汗が気化しないということがない限りは）汗が気化する先である「皮膚に接する空気の体積」に比例しますから、汗の影響も速度（レイノルズ数）のn乗に比例します。結局のところ、汗の影響を考えたとしても、放熱量は速度の0.△乗に比例する量になるわけです。

　自転車を漕ぐことで発する熱量は「速度の３乗に比例する」もので、そして、体から奪われる熱量は「速度の１乗未満に比例する」となると、自転車を漕ぐ速度を速くしていくと体内で発生する熱を放熱できなくなり・体がアッチッチになってしまう＝全然涼しくない…というわけです。

　自転車は「漕げば漕ぐほど涼しくなるわけではない」ようです。暑い日に、近くの街まで自転車を漕ぐ溶きはゆっくりゆっくり漕いでみるのが、一番暑くならない自転車の漕ぎ方かもしれません。

■箱根駅伝の途中棄権を生む「冬の強風は痩せ型に厳しい」理由　

　『箱根駅伝の途中棄権を生む「冬の強風は痩せ型に厳しい」理由』を書きました。

　 発熱量は１乗に比例し・放熱量は0.4乗に比例…ということは、（同じ体重で）体重が増えると発熱量の方が放熱量より遙かに多いけれど、体重が少ない痩せ型にとってはそうでない、ということになります。