2009-12-16[n年前へ]
■人間は論理・合理だけではうまくやっていけない 
 「阿川佐和子の会えばなるほど―この人に会いたい〈6〉 (文春文庫)
「阿川佐和子の会えばなるほど―この人に会いたい〈6〉 (文春文庫)
」中の、数学者というか、エッセイストの藤原正彦の言葉から。
藤原:人間は論理・合理だけではうまくやっていけないんだと。マルクスのような大天才が作った共産主義も論理的には非常に美しい。しかし、七十四年間、ソ連が実験して大失敗に帰した。それは人間と言う種には不適切だったからなんです。「理系サラリーマン 専門家11人に「経済学」を聞く!
2010-04-28[n年前へ]
2010-10-23[n年前へ]
■計算に困ったらkeisan へ 
 CASIO提供の数式計算サービス「keisαn」
CASIO提供の数式計算サービス「keisαn」
本サービスでは、独自の桁数可変演算技術を駆使し精度保証を追求した様々な計算ライブラリーがご利用いただけます。
「計算に困ったらkeisan へ」をキャッチフレーズに、「計算の正確さ、使い易さ、楽しさ」を追求しながら、ライブラリーの充実と計算への親しみを提供していきます。
2012-02-03[n年前へ]
■「2012年を表す3つの数式」と「生まれ年を表す数式」 
Wolfram Blogを読み、2012年を表す「3つの数式」を知りました。
10*9*8+7+6-5+4*321=2012 10+9*87-65+4*321=2012 109-8*7+654*3-2-1=201210からひとつづずカウントダウンを進めていくと、そして四則演算をしていくと…その結果が今年を表す2012になる、という数式です。
 こんな数式を眺めると、たとえば「自分の生まれた年」を表したらどんな数式になるだろう?と思ったりする人もいるかもしれません。…というわけで、 Wolfram Blogで作成されていた関数を使い、1950年から2011年までを表す数式を(それぞれ)ひとつずつ並べてみました。さてさて…あなたの「生まれ年」を表すのは、どんな数式でしょう。「あなたのためのカウントダウン数式」をメモしてみるのは、いかがでしょうか?
こんな数式を眺めると、たとえば「自分の生まれた年」を表したらどんな数式になるだろう?と思ったりする人もいるかもしれません。…というわけで、 Wolfram Blogで作成されていた関数を使い、1950年から2011年までを表す数式を(それぞれ)ひとつずつ並べてみました。さてさて…あなたの「生まれ年」を表すのは、どんな数式でしょう。「あなたのためのカウントダウン数式」をメモしてみるのは、いかがでしょうか?
10*9+8+7*65*4+32*1=1950 10+9+8*7*6*5+4*3*21=1951 10+98+7*65*4+3+21=1952 10-9*8+7/6*54*32-1=1953 10-9*8+7/6*54*32*1=1954 10-9*8+7/6*54*32+1=1955 10-9+8+7*6*54-321=1956 10*9*8-7*6-5+4*321=1957 10+9-8+7*6*54-321=1958 10-9+8+7+6*54*3*2-1=1959 10-9+8+7+6*54*3*2*1=1960 10-9+8+7+6*54*3*2+1=1961 10+9-8+7+6*54*3*2*1=1962 10+9-8+7+6*54*3*2+1=1963 10+9+8-7+6*54*3*2*1=1964 10+9+8-7+6*54*3*2+1=1965 10*9+8*7+65*4/3*21=1966 10*9*8-7-6+5*4*3*21=1967 10+9-8-7+654*3+2*1=1968 10+9-8-7+654*3+2+1=1969 10*9*876/5*4/32-1=1970 10*9*876/5*4/32*1=1971 10*9*876/5*4/32+1=1972 10*987*6/5/4/3*2-1=1973 10+9+8+7*6*54-321=1974 10-9+8+7+654*3-2-1=1975 10-9+8+7+654*3-2*1=1976 10*9-8*7+6*54*3*2-1=1977 10*9-8*7+6*54*3*2*1=1978 10*9*8+7*6*5*4*3/2-1=1979 10*9*8+7*6*5*4*3/2*1=1980 10*9*8+7*6*5*4*3/2+1=1981 10*9*8-7+6*5*43-21=1982 10+9-8+7+654*3+2+1=1983 10+9+8-7+654*3+2*1=1984 10+9+8-7+654*3+2+1=1985 10*9*8-7-6-5+4*321=1986 10*9*8+7/6*543*2*1=1987 10*9*8+7/6*543*2+1=1988 10+98*7+6*5*43+2+1=1989 10*98-76+543*2*1=1990 10+98*7+6+5+4*321=1991 1098+765+4*32+1=1992 10*9*8+7+6+5*4*3*21=1993 10*9-8*7+654*3-2*1=1994 10*9*8*7/6/5*4*3-21=1995 10*9*8-7-6+5+4*321=1996 10*9-8*7+654*3+2-1=1997 10*9*8-7+6-5+4*321=1998 10*9-8*7+654*3+2+1=1999 10*9*8+7-6-5+4*321=2000 10*9*8-7+6*5*43-2*1=2001 10*9*8-7+6*5*43-2+1=2002 10+9+8-7+654*3+21=2003 10*9*8-7+6*5*43+2-1=2004 10*9*8-7+6*5*43+2*1=2005 10-9+8*7*6*5+4+321=2006 10+98*7+6*5*43+21=2007 10*9*8-7+6+5+4*321=2008 10-9-8+7/6*54*32*1=2009 10*9*8+7-6+5+4*321=2010 10+9*8*7/6*5*4+321=2011
2012-09-15[n年前へ]
■「ルートを外して、色んなものを眺めてみたい」 
「n年前へ」から「ルートを外して、色んなものを眺めてみたい」
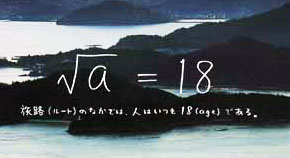
この数式で使われている"="は、いわゆる等号"= ="ではなくて、代入の"="かもしれません。つまり、この数式は「√a が 18 と等しい」ということを言わんとしているのではなく、「√aというものは全て18が代入される」という手順・代入式を意味しているということを意味しているのかもしれません。
それを、さらに素直に言い換えるならば、「旅路(Route)の中では、人は誰でも18(Age)になる」というコピー文そのままに変身します。 そういった「誰であっても18歳の頃に戻してしまう」ようなものが「旅路(Route)」なんだ、と高らかに定義・宣言する数式なのかもしれない…
さらに、「人のルート(Root=根底にあるもの)は、そんな18才の頃のようなものだよね」という強い意思を想像したのです。青春18切符のポスターに書かれた小さな式は、「旅は人を18歳の頃の気分にさせる。そして、それこそが - 人の根底- にあるものなのだ」と、そう伝えようとする言葉だと勝手に想像してみたのです。
■Powered
by yagm.net