1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
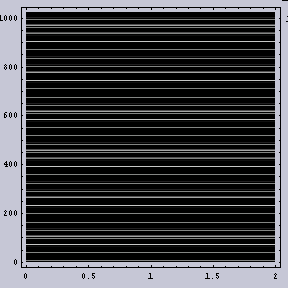
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
 |  |
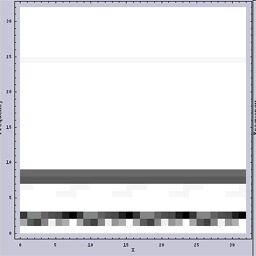
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
 |  |
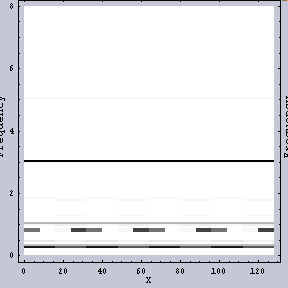
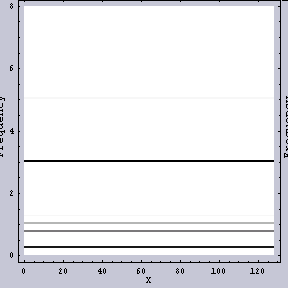
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
 |  |
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
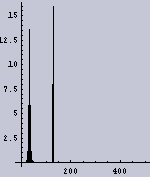 | 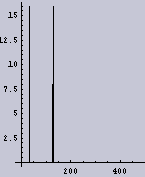 |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
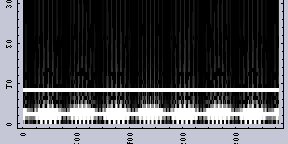 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
2005-05-19[n年前へ]
■品川から三島までの振動データの「時間 v.s. 周波数解析」 
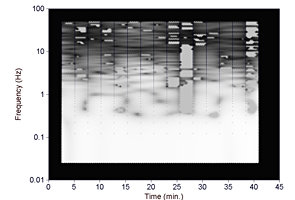
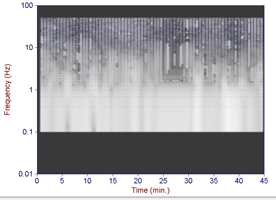
せっかくなので、下りのこだま585号 8号車 通路側のシート上の「品川駅から三島駅まで」の揺れデータ(10ms間隔)の時間 v.s. 周波数解析も短時間フーリエ周波数解析(高速フーリエ変換とは別物ですね)で行ってみました。横軸が時間軸で品から三島までを示していて、縦軸が周波数軸で振動の周波数を示しています。
左(or 上)のチャートで、時間軸(横軸)25分過ぎに現れる高周波数を多く含む振動は小田原で停車中に「ひかり」か「のぞみ」が通過した際の振動でしょうか? 確認しやすいように、短時間フーリエ変換ウィンドーサイズを小さくしたものを右(or 下)に示してみます。
 また、40分過ぎの激しい振動は熱海を出て箱根トンネルを通過中のものですね。…と、こんなことを調べても新幹線の振動が直ってくれるわけではないんですよね…。もうちょっと、快適にしてくれたら…良いなぁ。せめて、ハードディスク保護回路が働いたり、テーブルの上のコーヒーが倒れないくらいだったら良いなぁ。
また、40分過ぎの激しい振動は熱海を出て箱根トンネルを通過中のものですね。…と、こんなことを調べても新幹線の振動が直ってくれるわけではないんですよね…。もうちょっと、快適にしてくれたら…良いなぁ。せめて、ハードディスク保護回路が働いたり、テーブルの上のコーヒーが倒れないくらいだったら良いなぁ。
2016-12-23[n年前へ]
■Python/OpenCVで画像多重解像度解析コードを書いてみる 
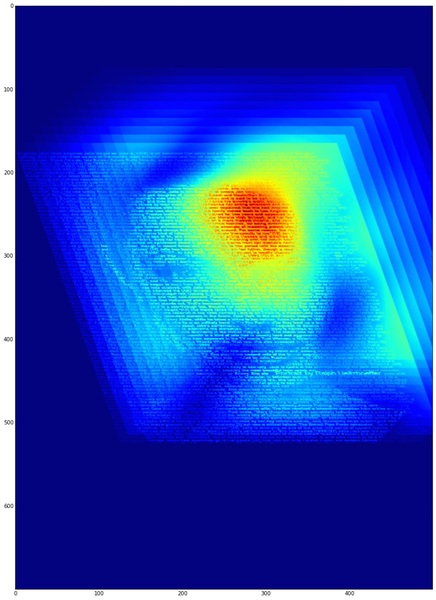 多重解像度解析…といっても直交基底に分解するというような話ではなくて、単に各周波数帯の特性がどの程度含まれるかを眺めるといった用途なら(つまり、ガボール変換やSTFTを掛ける感じの程度の用途なら)、Python/OpenCVを使って十数行で書けるかも?と思い書いてみました。もちろん、実装は簡単第一最優先!というわけで、ガウシアンフィルタ差分で2次元のバンドパスを作成し、それを周波数軸で重ねて眺めてみるというくらいの話です。
多重解像度解析…といっても直交基底に分解するというような話ではなくて、単に各周波数帯の特性がどの程度含まれるかを眺めるといった用途なら(つまり、ガボール変換やSTFTを掛ける感じの程度の用途なら)、Python/OpenCVを使って十数行で書けるかも?と思い書いてみました。もちろん、実装は簡単第一最優先!というわけで、ガウシアンフィルタ差分で2次元のバンドパスを作成し、それを周波数軸で重ねて眺めてみるというくらいの話です。
実際に書いてみたら、ポスト処理含めて約20行くらいになりました。超入門的な画像処理コードですが、1次元〜2次元の多重解像度解析や周波数解析を行うことは意外に多いような気もするので、適当に貼り付けておくことにします。*
*画像処理クラスタからのコメント:
・マルチスケールで眺めるなら、DCゲイン1同士のガウシアン差分をとり、そのL2ノルムを1に正規化しすべし。
・周波数軸は等比的にした上で、ボリューム的表示も等比的比率で重ねたい。
import numpy as np
import cv2
from matplotlib import pyplot as plt
def DOG(img, s, r):
img2=img.astype('uint16')
img2=img2*128+32767
gs = cv2.GaussianBlur(img2,(0, 0), s)
gl = cv2.GaussianBlur(img2,(0, 0), s*r)
return cv2.absdiff(gs, gl)
img = cv2.imread("sample2.jpg",0 )
(h,w)=img.shape
pts1 = np.float32([[0,0],[w,0],[w,h],[0,h]])
pts2 = np.float32([[0,h*1/4],[w*3/4,h*1/4],
[w,h*3/4],[w*1/4,h*3/4]])
M = cv2.getPerspectiveTransform(pts1,pts2)
baseImg = cv2.warpPerspective(
img.astype('uint16'),M,(w,h))
for i in range(100,5,-10):
pts1 = np.float32([[0,0],[w,0],[w,h],[0,h]])
pts2 = np.float32([[0+i,h*1/4-i],
[w*3/4+i,h*1/4-i],[w+i,h*3/4-i],[w*1/4+i,h*3/4-i]])
M = cv2.getPerspectiveTransform(pts1,pts2)
img2 = cv2.warpPerspective(DOG(img, i, 1.05),M,(w,h))
baseImg = cv2.addWeighted(baseImg, 0.9, img2, 0.3, 0)
plt.figure(figsize=(6,6))
plt.imshow(np.array(baseImg))
plt.autoscale(False)
