1998-11-18[n年前へ]
■スクリーンセーバー用の画像ファイルを作ろう。 
Canon in HongKong 1998
以前、作成した「FilmStrip」用の「画像ファイル集」を作った。テーマは- Canon in Hongkong 1998 - である。何故、Canonかというと深い意味はない。
ダウンロード 「FilmStrip」用の「画像ファイル集」- Canon in Hongkong 1998 - (Copyright Jun Hirabayashi)
上からダウンロードしたファイルを解凍し、できた"bmp"ディレクトリを"C:\image"ディレクトリの下に置く。つまり、"C:\image\bmp"という形になる。そうすると、「FilmStrip」から使えるようになる。今回のテーマを使うと、実行中の画面は下の図のようになる。
 |
このように、テーマを統一した画像ファイル集を使うのが、「FilmStrip」の作者としてのお勧めである。今回の画像の共通点と言えば、
- Canon
- 街
- 原色
今回のテーマの色合いは35mmリバーサルであれば、エクタクロームかベルビアといった所だろう。FinePix700のようなフィルム会社が出しているデジタルカメラの色特性(色再現性ではない)には非常に興味がある。コピー機メーカーと(オリジナルとしての)フィルムメーカーが出すデジタルカメラの色特性はもしかしたら違う傾向にあるかもしれない。コダックの出すフィルムが黄色(会社のイメージカラー)を強調し、富士写真フィルムのフィルムが緑(会社のイメージカラー)を強調していた、というのは本当かどうかはしらないが有名な話だ。そのような意図的な色特性があれば、それは個性として面白い。しかし、コピー機メーカーにはそのようなオリジナリティな発想はないかもしれない。いつか、それについても考えてみたい。
1999-07-05[n年前へ]
■目に映る明るさって何ですか? 
君は天然色
前回、デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、
- カラーから白黒への変換はどうする?
- セピアカラーって一体何だ。
- セピアカラーへの変換はどうやろう?
カラーから白黒への変換はどうする? どうしよう? これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。) 例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。
 |
とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。
いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。
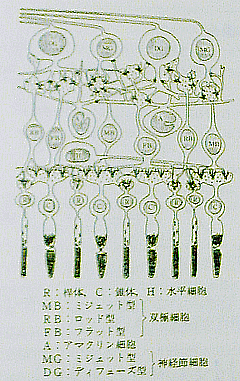 「視覚と画像」 大頭・行田 著 森北出版より |
それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。
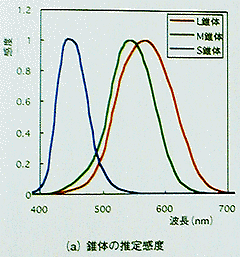 CQ出版 洪 博哲著 「お話・カラー画像処理」より |
次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。
 「視覚と画像」 大頭・行田 著 森北出版より |
後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。
というわけで、グレー化のために使っているのはこの式だ。
- Red: ptr[2]
- Green: ptr[1]
- Blue: ptr[0]、として
やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。
さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から
- 色に対する感じ方(眼とフィルム)( http://www.mmjp.or.jp/rwicp/data106.html )
- カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
- 明るさの見え方(明暗対比)( http://www.mmjp.or.jp/rwicp/data506.html )
- 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )
また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。
なお、以下のような答え方は遠慮致したい。
例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」
例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」
2002-08-17[n年前へ]
■高精度画像シミュレーションシステム開発と新規カラーリバーサルフィルムの階調・色再現設計への応用 
ꆡꓩꆣ짙믎볌뾿ꗕꖣꗫꗠꆣ
2007-04-28[n年前へ]
■Spectrum Color Conversion 

CMY<=>RGB の色変換の際に用いている基準は、「スペクトル強度の差の自乗和が最小になること」です。つまり、人の視覚特性などに特化した色変換ではなく、単純に分光強度の形状が近くなるような色変換を行っています。また、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルは非常に大雑把な値を使っています。特に、シアン・マゼンダ・イエローに関しては、印刷で用いられているインクとは異なり、比較的理想に近い吸収スペクトルの場合を示しています。もしも、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルを眺めてみたい場合には、RGBtoCMYやCMYtoRGBの入力値として、単色だけを255にして、それ以外の色を0にしてみて下さい。たとえばシアンだけがある場合の単色スペクトルを眺めたければ、シアン=255, マゼンダ=0、イエロー=0にする、という具合です。すると、その色だけを使った時のスペクトルを見ることができるわけです。ただし、減産混色の場合に表示されるのは、いわゆる吸収スペクトルではなく、インクに吸収されなかったスペクトルということになります。また、CMYが示している量には対数変換がかけられています。
RGBtoCMYとCMYtoRGBは、相互に入力スペクトルと再現されたスペクトルを比較することもできますから、RGBとCMYの間で相互に色変換を繰り返しながらスペクトルの変化を眺めてみるのも面白いかもしれません。
なお、このSpectrum Color Conversion は、離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージをWolfram Technology 社のMathematica上で作成し、webMathematica エンジンを用いることで、web アプリケーションとして動作しています。