hirax.net::Keywords::「関数」のブログ

■Photoshopプラグイン開発環境(PDLS)再び　

　Photoshopプラグイン開発環境 Photoshop DLL Linking System (PDLS) のページを(旧Pukiwiki)のファイルを元に書き直しました。PDFの説明ファイルの2004/08/07版はこちらになります。また、サンプルソース・バイナリファイルはこちらです。

　AmetMultiのモットーは「ATOKから何でもできる」でしたが、PDLSのモットーは「Photoshopから（その人のレベルに応じて）何でもできる」でした。(Photoshopの規約は気にせず)Cを使ってネイティブ・プラグインを気軽に書くこともできれば、GUIを使った連続作業などで自動的にマクロ関数(プラグイン)をお手軽に作ることもできる。その人のレベルに応じて、ステップアップすることができるPhotoshopのプラグイン開発環境というわけです。

　マクロ関数やネイティブ・プラグインを組み合わせれば、さらにカスタムプラグインを作ることもできます。また変数を使ったり演算や数式処理も使えて、NEWやDELETEといったマクロを使い、局所領域に対してだけ演算を行うこともできます。そして、マクロプラグインには自動的にGUIをかぶせることもできるのです(GUIコードを書かなくても、ダイアログで変数設定などを実行時にすることができる)。

　また、表計算アプリとの連携や鳥瞰図表示のプラグインもついている……というテキトーな機能てんこ盛り、の環境です。Photoshop Elementなんかで使うこともできますので、画像処理で遊んでみたい人は一度使ってみても良いかもしれません。いつものように、SYSTEMコールもできるプラグインなので、つまりは何でもし放題のプラグイン環境です。使ったことのないPhotoshopユーザ（ないしはPhotoshopプラグイン互換の画像処理ソフトユーザ）は一度遊んでみると良いかもしれません。

■「爆乳でなくなったら歩けない」を科学する　

　「爆乳」という言葉の名付け親と「メガ乳」という言葉の名付け親と話をした時に、「新鮮に聞こえるが普遍的にも聞こえる」話を聞き、面白さを感じた。そんなことを感じた話のひとつが、こんなことである。

　（IとかKカップとかいった爆乳の女優さんの多くが言うことには）「バストが小さくなったら、歩き方がわからない」「もう歩けなくなってしまうかもしれない」

　2kgほどの重量物を胸部に二つも可動する状態で歩こうとしたなら、「重量物の揺れ・振動」を抑えつつ、それでも抑えきれない重量物の揺れと共存した歩き方にならざるをえないはずだ。つまりは、大きなバストがあること前提の歩き方になっているに違いない。だから、「バストが小さくなったら、歩き方がわからなくない」ということになるのだろう。

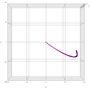
　ところで、可動する重量物、端的に言えば・揺れるバストは、下に描いたようなバネ・ダンパモデルとして単純にモデル化することができるだろう。つまり、その図の下に書いた微分方程式で表されるダイナミック・システムである。あるいは、それを伝達関数モデルにまでしてしまえば、つまりはさらに下に描いた「２次遅れ要素」である

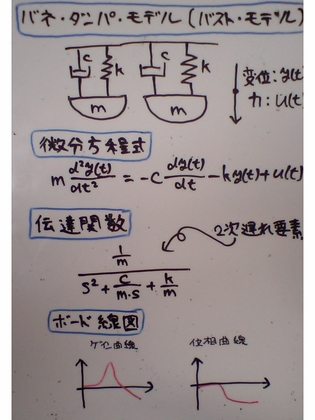
　電気のRLC回路（発振回路）なども、上の微分方程式と同タイプの式で表現される。そして、発振回路でコンデンサの容量（Ｃ）がいきなり小さくなってしまった場合などは、当然ながら発振周波数も変わり、その結果、回路の動きは大きく姿を変えることになる。つまり、「容量が小さくなってしまったら、（それまでの動かし方では）回路が動かなくなってしまう」という状態になるわけだ。

　つまり、上に描いた「メガ（爆）乳」を表現したダイナミック・システムと電気回路の間には、類似性（アナロジー）があって、それらは共通の普遍性を垣間見せるわけである。

　だから、実は、電気工学や機械工学のエンジニアたちこそが「爆乳の女性人たちが経験的に会得した歩き方の工夫」の一番の理解者になったりするかもしれない、と思ったりもするのである。「そうそう部品の定数がいきなり変わったら困っちゃうよね」と大いに共感できそうなきもするのだ。……もちろん、そんな妄想に「そんなわけない」とすぐに突っ込みたくもなるのだが。

■光スペクトル操作用のMathematicaライブラリ　

以前、Mathematicaの演習用に作った「スペクトル操作用Mathematicaライブラリ」を少し直したので、ここ（”ColorLib_amature.nb”に置いておきます。以前作ったものと同じく、スペクトル・データをリストのような離散データではなくて、関数として（純関数＝無名関数として、あるいは、明示的な関数として）取り扱うという点が特徴だと思います。「（せっかくMathematicaで解くのですから）解析的に解く」「使用者には離散化・数値計算など、面倒くさい汚い部分は見せない・見たくない」という方針で作ったものです。

以前のものからの変更点としては、"spectorPlot"や"labPlot""labColorPlot"など、関数名のMathematicaの命名規則に合わせた変更、加法混色・減法混色用関数の追加・グラフ表示関数の追加・バグ修正といったところです。

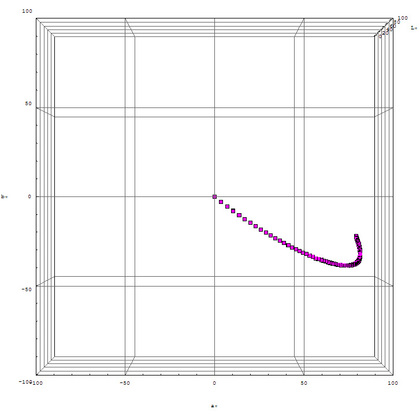　最初のラフスケッチが、絵画の原理を自分なりにおさらいするためのものだったので、濃度変調・面積変調などを扱おうとする場合には、比較的簡単に・気持ち良く作業ができると思います。たとえば、下記のようなコードを書けば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の具合を CIE Lab 空間で眺めたりすることができます。

labPlot[
　Map[lab,
　　Table[transmissionSpector[D65,
magentaFilter, d],{d,0,10.0,0.1}]
]
];

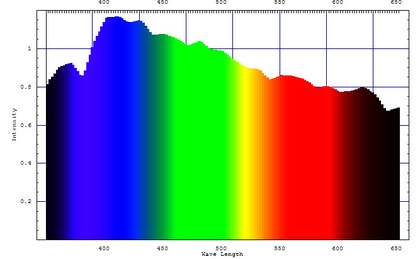　また、白色光照射時に黄色い絵具を塗り拡げる面積を増やしていった場合の反射光スペクトル変化をアニメーションとして作成・グラフ表示するコードはこんな感じです。"addtiveMixtureSpector"は加法混色用の関数で、"transmissionSpector"は減法混色用の関数です。お遊びソフトですが、色々遊ぶこともできるかもしれません。

Map[spectorPlot,
Table[
addtiveMixtureSpector[
{whiteLight,
transmissionSpector[whiteLight, yellowFilter, 1]},
{1-r, r} ],{r,0,1,0.1}]];

　コードを書く際に、Mahematicaで数式と文字列をシームレスに取り扱うことができたなら、もっと簡単に関数が書けるのにとも感じました。しかし、そういった感覚になるときは、たいていの場合「その道具の使い方・その道具を扱うプログラミングスタイルが間違っている」ことが多いものです。というわけで、Mathematicaプログラミングをまた勉強しなおしてみよう、と思ったのです。

■「スペクトル操作Mathematicaライブラリ」で動画を作る　

　光スペクトル操作用のMathematicaライブラリで、スペクトル変化の動画を作ると、こんな感じになります。Map　も　spectorPlot　も　Table も addtiveMixtureSpector　も whiteLight も cyanFilter も・・・どれも「関数」です。addtiveMixtureSpector　や whiteLight や cyanFilter は「関数を返す関数」で、Map などは関数を引数にとる関数です。Mathematica でコードを書いていると、なぜか自然に関数を重ね合わせていくような書き方が気持良くなってきます。

Map[spectorPlot,
　Table[
　　addtiveMixtureSpector[
　　　{whiteLight,
　　　transmissionSpector[whiteLight,
　　　cyanFilter, 1.0]}, {1-r,r}]
　,{r,0,3,0.05}]]

　それで、今この瞬間の悩みはMathematicaで"spectorFitting[targetSpector_,usingSpectrum]"というような関数をどうやって書くか、ということです。targetSpector は、任意のスペクトルを表現する関数で、usingSpectrum は「スペクトルを表す関数群」で要素数は任意のリストです。usingSpectrumを使いtargetSpectorをどのように表現するかを、最小二乗近似で最適解をNMinimize で解くというのが、そんな関数を作るときの定番の手順なのだろうと思います。つまり、方程式と制約条件を動的に作成し、それをNMinimize で解いた結果を返す、という具合です。

　さて、この　spectorFitting という関数はどう簡単に書くことができるものでしょうか。Mathematicaは変数名と文字列を明確に区別する割に、見た目ではまったくその違いがわからないのが面白いところ（同時に苦労するところ）かも、と思ったりしたのです。

■「肌」と「昼の日差し」のスペクトル　

　夏の日差しを実感するようになりました。肌は日焼けして赤黒くなり、そんな肌はピリピリと痛く、熱っぽさすら感じます。そんな、夏の明るい景色を眺めていると、なぜか楽しくなります。

　痛いけれど日焼けする夏の日差しが気持良く感じる人もいる一方で、日焼けする夏を嫌う人も多いと思います。特に日焼けしたくない女性にとっては、夏は面倒でとても嫌な季節だったりするのかもしれません。

…と考えているうちに、ふと、夏の日差しを浴びる「肌の色」を眺めてみたくなったのです。そこで、２週間ほど前に作った「光スペクトル操作用のMathematicaライブラリ」にいくつかの色関数（スペクトル吸収関数）を追加してみました（サーバからダウンロードできるライブラリ更新は数日後になります）。追加したスペクトル吸収関数は、「血液」「カロチン」「メラニン」…といったもので、皮膚内部にある物質の吸収スペクトルを表現するための（単純化した）スペクトル関数を実装してみました。

　そういった色関数を組み合わせると、いろいろな「肌色」を眺めることができるます。たとえば、右上の図は、(どの波長も均等に含んでいるような)白色光源で照らした時に血液の反射スペクトルがどう見えるかを試しに計算してみたものです。

spectorPlot[transmissionSpector[
whiteLight, bloodColorFilter, 0.5]
]];

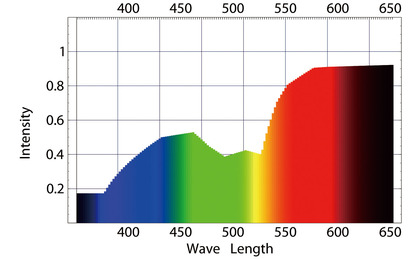
　ところで、こんな「色関数」を作り、適当で大雑把な「肌」を作って眺めてみました。すると、色温度6500ケルビンの標準光源、すなわち自然な昼光光源であるD65で、肌色を形作るメラニンや血液を照らしてみると、意外なほど「反射スペクトル」が平らになるものだ、と気づかされました。

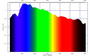
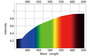
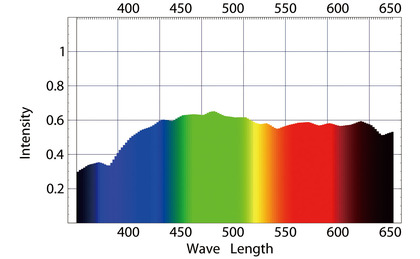
　つまり、昼の日差しのスペクトルのうち、スペクトル強度が強い短波長領域では、メラニンや血液などの色吸収率が高く、その一方、「昼光」のスペクトル強度が低下する長波長域では、メラニンや血液などの色吸収率が低く、それらの結果として反射スペクトルが”結構”均等になるのだなぁ、と感じたのです。たとえば、右のスペクトルグラフが、昼光＝D65光源で皮膚を照らした時の反射スペクトルの例になります（ちなみに、右下のグラフがD65光源のスペクトルです）。

　それは、単に長波長領域の光は皮膚中で吸収されることが少なく、短波長の光が吸収される、というだけのことでしょうし、さらには、人によってメラニンの分布量・形状が異なり、反射スペクトルは全然違うわけで、こんな結果も一般的なものでは全くありません。

　けれど、「昼光の逆関数のような、まるで、強い日差しから身を守るかのように最適化されたような皮膚の吸収スペクトル」を適当に作ったライブラリ関数が生成したのを眺めたとき、とても不思議なくらい新鮮さ・意外な面白さを感じたのです。