2007-04-14[n年前へ]
■Icosahedron Worlds 
 "Icosahedron Worlds" は、好きな画像ファイルから、のりしろなども付いた正二十面体の展開図を作成するWEBサービスです。あなたの手元にある画像ファイルを、ブラウザ画面からアップロードするだけで、自動的にサーバー内で画像変換が行われて、ブラウザ画面に正二十面体の展開図が表示されます。表示された正二十面体の展開図を印刷すれば、あなたの画像ファイルを実際の正二十面体として組み立てることもできます。
"Icosahedron Worlds" は、好きな画像ファイルから、のりしろなども付いた正二十面体の展開図を作成するWEBサービスです。あなたの手元にある画像ファイルを、ブラウザ画面からアップロードするだけで、自動的にサーバー内で画像変換が行われて、ブラウザ画面に正二十面体の展開図が表示されます。表示された正二十面体の展開図を印刷すれば、あなたの画像ファイルを実際の正二十面体として組み立てることもできます。
処理された展開図は、ブラウザ上では一見小さな画像に見えます。しかし、実際には非常に大きなサイズの画像ファイルです。画像上でマウスを右クリックでもすれば、展開図の画像ファイルをローカル・ディスクに保存することができます。ダウンロードした展開図を好きなサイズでプリンターから印刷すれば、好きな大きさの正二十面体を作り出すことができます。

今のところ、サーバにアップロードした画像ファイルを削除する機能はありません。そのかわり、アップロード時に自動的に暗証番号が付加され、その暗証番号を指定しなければ、アップロードした画像にアクセすることはできないようになっています(たとえば、アップロード後に表示されるhttp://www.hirax.net/map/index/16?code=186604のcode=186604の部分がその暗証番号です)。もしも、アップロードして作成した画像や展開図に、後でアクセスしたい場合には、ブラウザ・アドレスバーに表示されているURIをメモするなどしておいて下さい。このhttp://www.hirax.net/map/index/16?code=186604というアドレスを他の人に知らせたならば、手元の写真を正二十面体の展開図にしたものを友達に見せることもできます。友達と一緒に撮影した写真などを「展開図」にして、見せてみるのも楽しいかもしれません。友達の顔をした正二十面体を作るのも面白いかもしれません。一枚の写真から、掌の上にのる小さな世界を作る、"Icosahedron Worlds" は、そんな風に1枚の2次元の画像から、いろいろな面を持つ3次元の空間を作り出すWEBサービスです。
2008-03-22[n年前へ]
■JRチケットの磁気データを眺めてみる 
 ICカード化されているSUICAなどと違って、通常のJR切符などは、裏面の磁気データで管理されている。右に貼り付けたのは、JRの切符ではなくて領収書だけれど、基本的には通常のJR切符も、同じサイズであるし、同じような仕組みになっていると思う。
ICカード化されているSUICAなどと違って、通常のJR切符などは、裏面の磁気データで管理されている。右に貼り付けたのは、JRの切符ではなくて領収書だけれど、基本的には通常のJR切符も、同じサイズであるし、同じような仕組みになっていると思う。
このJRが発行したチケットの裏面に書き込まれている磁気データを、磁気微粒子粉末で可視化して、2次元画像に変換してみたものが下に貼り付けた画像である。上下4行づつ、計8行の磁気データが書き込まれていることがわかる。この磁気データを眺めた時、興味深く・面白いことは、チケットの中心を軸にして、線対称に上4列と下4列に対して同じデータが書き込まれているように見えることである。

逆に言えば、磁気データは本来4列ですむのに、それを上下部分に同じように書き込まれているように見えるのである。これは、「磁気読み取りヘッド数を減らしつつカードリーダにチケットをどの向き(もちろん長短辺は一致している必要があるが)で挿入しても大丈夫なようにするために、そのような設計になっている」のだろうか。それとも、そんな単純な理由ではなくて、もっと複雑な理由によるものだろうか。
日常生活を支えているシステムはたくさんあるけれど、それらが動いている仕組みがちゃんとわかるものは、ほとんどないように思える。そういったシステムの裏側をミステリの謎解きのように想像してみるのも、結構楽しい。
2008-04-25[n年前へ]
■「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描く 
複素平面"complex plane"は、複素数"complex number"の実部をx軸(実軸=real axis)・虚部をy軸(虚軸 = imaginary axis)にプロットしたものである。3+2iという複素数であればxy平面にx=3,y=2にを示す、そんな平面が複素平面だ(iは虚数単位=2乗した時に-1になる数である)。
『「仕事」と「趣味」を2次元マップで1分以内に描け』言われたら、あなたならどう描くだろう?(同世代の)"Schemeを愛するプログラマ"が描いた「趣味と仕事の関係を描いた2次元チャート」を眺め、ふと私も「仕事」と「趣味」のイメージを2次元マップに描いてみたくなった。
趣味を訊かれるといつもちょっと困る。私には趣味と仕事の違いがよくわからないからだ。
Shiro Kawai
人によって「仕事」と「趣味」というものの捉え方は違うだろうけれども、できる限り一般的に「仕事」と「趣味」という領域を2つの軸上に配置させるとしたら、どのように「仕事」と「趣味」を描くだろう?そんなことを「クイズの回答者になった気分で」描いてみたら、それは「複素平面」だった。(その人自身に対する)実利的・物質的でまさにリアルな"Real axis"と、イメージ的な「心の軸」を示す"Imaginary axis"というまさに実軸・虚軸で表現された複素平面である。
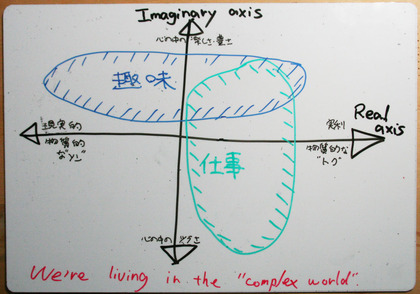
この複素平面の縦軸(の上方向)は、自分の心を豊かにする軸と捉えることができるだろう。「虚」という文字よりは、"Imaginary"という文字で捉えたい「(その人自身の)心の満足」を示す軸、である。
そして、横軸(の右方向)は、その人自身を実利的に満足させる軸である。しかし、その自分への「実利」という軸は、実は他人が何らかの形で価値を感じたことを示す軸でもあると思う。なぜなら、その「実利」は「他者が得た価値」が回りまわって流れてきたものに違いないからである。他人が得た満足が姿を変えたものであるから、である。つまり、この複素平面の横軸は「自分への実利」を示す軸であると同時に「他者を豊かにする軸」なのである。
ひとことでまとめてしまえば、この複素平面は「本人(自分)の満足」と「他人の満足」という2つの軸で形作られる平面なのだ。
'Cause we are living in a material world. You know that we are living in a material world.
Madonna "Material Girl"
その人ごとに「仕事」と「趣味」の位置づけがあると思う。どんな軸を使って、どんな風に「仕事」と「趣味」を捉えるかは、みなそれぞれ違うはずだ、と思う。「自分の中で辛さを感じながら、実利を得る仕事」もあれば(右下の象限)、「自分自身の楽しさとともに実利を得る仕事」もあるはずだ(右上の象限)。そして、さらに言うならば、同じ仕事であったとしても、その仕事がどこに位置するかは、人それぞれ異なっているだろう、と思う。そして、同じ一人の人がする同じ仕事であったとしても、きっと「その捉え方」「その座標」は変化し・移動していくものだろう、と信じている。
俳諧で「虚実」ということがしばしば論ぜられる。数学で、実数と虚数とをXとYとの軸にとって二次元の量の世界を組み立てる。虚数だけでも、実数だけでも、現わされるものはただ「線」の世界である。二つを結ぶ事によって、始めて無限な「面」の世界が広がる。
寺田寅彦 「無題六十四」
もしも、上に描いた複素平面="Complex plane"、それを言い換えれば言葉通りの「複雑極まりない世界」の上に、今のあなたが抱えているだろう「仕事」と、あなたが楽しんでいるかもしれない「趣味」は、どんなXY座標上にプロットされるだろうか。"複雑極まりない"複素平面上に、あなたはどんな軌跡を描いているだろうか。
2008-05-22[n年前へ]
■グラビア写真の「体積」と「面積」の大きさ感覚 
 当たり前のようだが、体積と面積は次元が違う。たとえば、「満腹30倍」ダイエットキャンディのヒミツでは、こんなことを書いた。
当たり前のようだが、体積と面積は次元が違う。たとえば、「満腹30倍」ダイエットキャンディのヒミツでは、こんなことを書いた。
体積で30倍ということは、長さでは3倍程度に過ぎない。つまり、「縦3倍×横3倍×高さ3倍≒体積30倍」というわけである。「体積が30倍でも長さは3倍程度に過ぎない」というこの当たり前の「意外さ・齟齬」は、次元にまつわる色々なことに対して当てはまる。
グラビア写真を撮影するカメラマンいわく、
実際に見ていると、胸がとても大きく感じるモデルを撮影していても、写真にしてしまうとその大きさがあまり感じられなくなってしまう。なぜか、胸が小さく見えてしまう。だという。実際に三次元の物体を眺めている時に感じる巨大さを、二次元の画像で眺めてしまうと、あまり巨大には見えなくなってしまうのだ、というのである。
「体積が30倍でも長さは3倍程度に過ぎない」ということは、体積が30倍の立方体は、面積では3x3=9倍程度に過ぎない。半球で言えば、体積が2倍もある半球であっても、断面部分の面積に換算してみれば、それは1.6倍に過ぎない。
つまり、バストのような3次元の半球状物体を、2次元平面で把握してしまうと、三次元立体として把握したときに比べて、「大きさ」がかなり小さく感じられてしまうのだ。
たとえば、グラビアカメラマンの立場からすると、この違いは大問題に違いない。
「(体積や面積といった)次元」と「グラビア写真」という一見関係なさそうに見えるものも、実は密接に繋がっている。無味乾燥に思える教科書に書かれていることで、グラビア写真集を写している人たちの苦労が想像できる、ということが意外で面白い。
2008-07-18[n年前へ]
■エクセルでシミュレーション Vol.1 [静電界準備 編] 
 「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは(私たちのような勉強世界からの REST OF US にとっては)とても素晴らしいと思います。
「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは(私たちのような勉強世界からの REST OF US にとっては)とても素晴らしいと思います。
ところで、現在では”表計算プログラム=マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。
 自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」をしてみました。
自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」をしてみました。
まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。2次元世界を離散化するということは、エクセルの表がそうであるように「世界(画面)をセルで分割する」ということです。

上で(x,y座標空間での)差分方程式にしたものを、さらにエクセル(表計算ソフトウェア)で解くときのやり方を図解したものが下の図です。「ある点の電位(φ)は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。
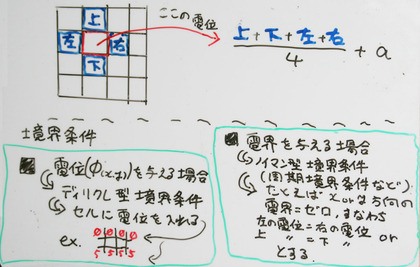
また、2種類の境界条件(電位を指定するディリクレ条件/電界を指定するノイマン条件)をどのようにエクセル上で処理するか、というのが下の部分になります。
こういったセルの値が「(そのセル自身を含む)セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。

以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。