hirax.net::Keywords::「PID」のブログ

■解析機能付きPID制御やモデル予測制御機能を備えた制御系設計/シミュレーションツールを発売　

　「解析機能付きPID制御やモデル予測制御機能を備えた制御系設計/シミュレーションツールを発売 」
　最適PIDゲイン値探索ツールとMIMOコントローラ構築のための補助ツール。日本ＮＩ、解析機能付きＰＩＤ制御など備えたシミュレーションツールを発売といったプレスリリースを読むと、システム同定やSimulinkモデルをLabViewに接続することがでたり…と、ユーザの悩みを減らすような感じなのだろうか(逆に言えばベンダ側の辛い切磋琢磨が生まれているのだろうか)。

■加速度P(I)D制御の防振エディタ　

　列車や飛行機や、あるいは、船の上といった場所でPCを使う人もいる、と思います。そんな人たちは、とりたてて多くはないのかもしれないけれませんが、きっと、そんな人たちもいると思います。つまり、揺れ動くノートPCの液晶を眺めながら作業をする人たちがいると思うのです。

　そんな作業は、目を疲れさせ、きっと視力を悪くします。・・・そこで、ノートPCに搭載されている加速度センサを使って、揺れの成分を取り除くようにWindowを動かすエディタを作ってみた。題して、「加速度P(I)D制御の防振エディタ」です。つまり、その瞬間の加速度=位置の差(Propotional)と、その瞬間の加速度の微分=位置の差の差(Differential)をさらに演算した結果を用いて、エディタのウィンドー位置を防振補正し、「揺れ動く環境の中でも目を疲れさせないエディタ」を作ってみたのです。

　そんな「加速度P(I)D制御の防振エディタ」を使っているようすを撮影してみました。それが、上に貼り付けた動画です。画面中央右の「加速度P(I)D制御の防振エディタ」が、その他のWindowsパーツと違って、防振の方向に動いている（動かそうとしている）のがわかるだろう、と思います。

ちなみに、その拡大動画が下に貼り付けたものです。画面右が防振エディタで、画面の左後ろにあるのが普通のエディタになります。
　ケータイで撮影した動画ではわかりづらいと思いますが、真面目にやれば効果が結構あるように思えるのです。・・・ということは、あと数年もすると、「加速度P(I)D制御のノートPCの防振表示画面」というものも、ごく当たり前になっているかもしれません。

■エクセルでシミュレーション　Vol.10　二次元非定常熱伝導問題シミュレーション＋P(ID)制御エクセルシートを作ってみよう　

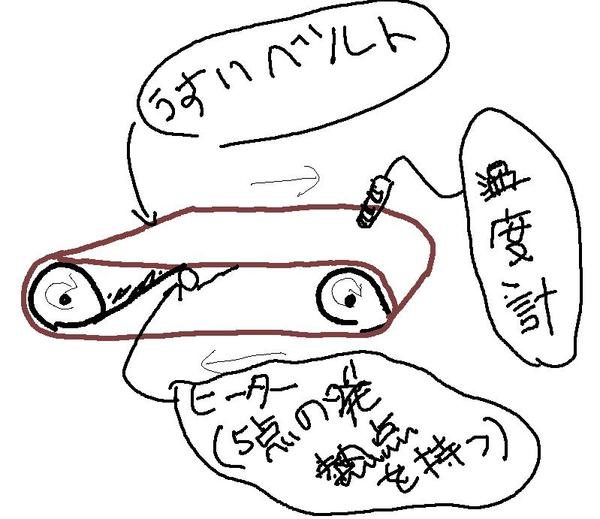　「エクセルでシミュレーション　Vol.9　二次元非定常熱伝導問題の温度変化グラフも作ってみよう」で、二次元非定常熱伝導問題を解くシートを使いながら（実用的範囲では三次元問題と大差がない）、ヒーターで回転するベルトを高温にした場合の、その回転ベルトの温度分布がどのように変化していくかを計算し、グラフ化し、さらにベルト中の一部分の温度を時系列的にモニターする機能を付けた、シートで遊んでみました。

　そこで、今回は、センシングしたベルトの温度を用いて、ヒーターの温度を簡単なPID制御を使ってフィードバック制御するエクセル・シートを作ってみることにしましょう。

PID制御とは、調整量を（現在の）出力値と目標値との差に比例＝Proportionalした量、その（過去からの）積分=Integralに応じた量、および（その瞬間に次にどのように変化するかという）微分=Differentialに応じた量にしたがって変える制御です。言いかえれば、現在（Proportional）・過去（Integral）・未来（Differential）の挙動に応じて、制御調整量を変えてやろうという制御です。比較的、古典的な制御手法ですが、現在でも、もっとも一般的な制御手法です。

　まずは、前回のエクセル・シートでヒーター部分を単純に（計算をさせ始めてから＝回転ベルトに対するヒーターを動かし始めてから）100℃にし続けた場合の計算過程を示してみます。つまり、何の制御もしない場合です。その計算結果が、下の動画です。上の動画で上に示したグラフが、回転ベルトの温度分布を示したグラフです（回転ベルトを切り開いたように温度分布を示しています）。動画中の下の折れ線グラフは（上のコンター図で灰色丸部の温度の時間変化を示したグラフです）。ちなみに、縦軸は0℃から150℃までで、横軸が時間軸です。

　下の折れ線グラフを見れば、上のコンター図で灰色丸で示した部分の、温度が時間に応じて上昇し、やがて100℃近くになっていることがわかります。

　さて、次にPID制御を行ってみることにしましょう。…とはいえ、最初は簡単のために、「灰色丸で示した部分の温度と目標調整温度である100℃との差をヒーターに足す（ネガティブ・日―ドばっく）」という「P=比例成分=現在の違い」だけを利用したP(ID)制御を行ってみます。つまり、現在の出力と目標出力の差異のみをヒーター出力に（適当な比率で）足し合わせてみるのです。言いかえれば、ベルトの温度が0℃なら、ヒーターを200℃くらいにすることで、急激にベルトを温め温度を調整し、目標温度100度と現在のベルト温度の差が小さくなってきたら、ヒーターの温度を110℃くらいに変えてやる・・・というような制御をしてみます。そんなシミュレーション計算を行ってみた結果が、下の計算結果になります。ちなみに、ヒーターの制御温度はエクセルのシートでB32セルで計算されています。また、灰色丸のセンサ取り付け部分（を示した）の温度を示す下の折れ線グラフは、先ほどと同じく、縦軸は0℃から150℃までの温度を示し、横軸が時間軸となっています。

　この結果動画を見るとわかるように、「P=比例成分=現在の違い」だけを利用したP(ID)制御（=積分成分と微分成分を使わない）制御では、ベルトの温度は早く立ち上がりますが、ベルトの温度は振動して、なかなかすぐに安定してくれません。しかも、早く温度を立ち上げようとすると、温度振動は大きくなってしまい、温度振動を防ごうとすると、なかなか温度が早く立ち上がってくれない、という相反する関係になっています。いわば、（ある程度、減衰がある）強いバネと弱いバネの振動と同じような現象が起きてしまいます。

　さて、それでは、一体どうしたら良い制御ができるのでしょうか。・・・せっかく、簡易にエクセルのような（表計算＝スプレッドシート・ソフトウェアを使った）熱伝導方程式を使ったシミュレーション計算を行うことができる環境があるわけですから、今回扱ったPID制御のような古典的な制御をもう少し復習してみようと思います。

　そして、せっかく熱伝導方程式を計算してみたりしているわけですから、そういった微分方程式（つまり現在から未来を示す式）を使うことで実現できる、最適化制御についても考えてみることにします。