hirax.net::Keywords::「オブジェクト指向」のブログ

■Mathematicaで「オブジェクト指向風」記述　

　春過ぎの頃、「分光スペクトル・色処理用のMathematica 7.0用ライブラリ」を作りました。そのライブラリを使うと、たとえば、D65光源下で、赤紫色の絵具を重ね塗りしていく際の色変化を CIE Lab 空間のグラフで表示させると、

labPlot[ 
  Map[lab,Table[
           transmissionSpector[D65,
                   magentaFilter, d],
                   {d,0,10.0,0.1}]
     ]
]; 

というようなコードになります。labPlotという名前の関数が一番外側にいて、その内側にMap関数がいて、さらにその引数のひとつにTable関数がいて、その内側にtransmissionSpectorがいて・・・、という風に関数・括弧で外側から包まれているような具合の書き方になります。

　こういう書き方をしていると、括弧の対応がわからなくなったり、処理の流れがわからなくなったりしてしまうように感じることがあります。そんな時、気分転換がてら、Mathematicaのコードを「オブジェクト指向風」記述で書き直したりします。どういうことかというと、たとえば、こんな関数を定義してやります。

Light[new]:=Module[
  {Spector=D65,
   self},
  self[setSpector,spector_]:=(Spector=spector;self);
  self[spector]:=Spector;
  self]

　すると、

a=Light[new][setSpector, D65][spector][600]

というように記述をすることができます。これは、スペクトル属性を持つ「光オブジェクト」をつくり、そのスペクトルをD65光源と同じにし、そのスペクトルの600nm波長の強度をaに代入する、という内容です。最初の例のような、括弧で多重に囲われているのではなく、括弧が連続しているので、括弧の対応や処理手順がわかりやすくなっています。

　コードのミソは、「Module内で宣言した（一意に識別できる名前が付けられる）変数self」により、オブジェクトを表現している、というところです。また、selfを返す関数を作ることにより、Light[new][setSpector, D65][spector][600]という風に処理を連ねていくことができるわけです。

　もちろん、こういう「オブジェクト指向風」記述をわかりやすく感じる時もあれば、そうでない場合もあるわけで、状況によって、あるいは、その時の気分で好きな風に書く、のが趣味プログラミングとしては一番楽しいような気がします。

■Mathematicaライブラリをさらに「オブジェクト指向風」にしてみました　

　以前、分光スペクトル・色処理用のMathematicaライブラリ（関数群）を作りました。そして、この前Mathematicaで「オブジェクト指向風」記述をすることで、括弧の対応や処理手順を見やすく・わかりやすくしてみました。もちろん、「わかりやすい」というのはあくまで主観的な話です。

　今日は、もう少し本格的な例を作ってみようと考えて、そのMathematicaライブラリに、Spectorクラス・Layerクラス・Lightクラスを作成・追加してみたのです。物体を光で照らした時に見える分光スペクトルを、モンテカルロ的に解く機能を適当に付けてみました。

　そんなわけで、スペクトルを扱うSpectorクラス、立体形状を扱うLayerクラス、そして、適当に光追跡を行う機能を盛り込んだLightクラスを仕立ててみたのです。

　たとえば、デフォルト設定をそのまま使うなら、

layers=Layer[new]
aLight=Light[new]
aLight[in,layer][showTrace]

といったコードを書くと、三次元物体中を照らす光の色が、どのように変わっていったかを立体的に表示させることができます。

　あるいは、

Spector[new][set,blueSpector][spectorPlot]

と書けば、青い色のスペクトル分布を描いてくれます。Layersは・・・形状を定義する関数を少しオブラートに包んだクラスです。

そんなわけで、数日後には、バグ確認・使い方の例などを加えた上で、サイトからダウンロードできるようにします。また、適当に仕立てたこのツールを使い、何か解析でもしてみようと思います。

■Mathematicaで発色シミュレーションをオブジェクト風記述にする　

　Mathematicaで発色シミュレーションをモンテカルロ法で行うライブラリを作りました。オブジェクト風記述にできるのが特徴です。（今週末まで修正作業を行うつもりなので、多少、仕様は変わるかもしれませんが）たとえば、

Light[new][in,Layer[new]][showTrace]

という記述をすると、下のグラフのような、三次元構造の中で反射・屈折・散乱を行う「光」のスペクトルが、どのように変化していったかを知ることができます。

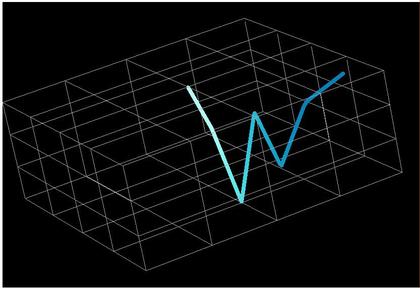
　この例の場合は、Layer[new]で、デフォルトのコンストラクタで作成された水色の層に入射した光の挙動を眺めてみたものになります。層内で多重反射した後に、水色に染まって層の外へ出て行ったことがわかる、という例になります。

　ライブラリは、週末にサイト上へアップロードする予定です。

■開発言語「Scala」ベースのJavaプログラミング環境「Scalalab」　

　開発言語「Scala」ベースのJavaプログラミング環境「Scalalab」

　オブジェクト指向言語のScalaをベースに、高レベル運用機能と統合環境を加えることで、JVM向けの学術的なプログラミング環境構築を目指す。 Matlab／Scilabスタイルの学術的コンピューティングプラットフォームプロジェクト「jLab」の姉妹プロジェクトとなり、jLabも Scala言語にマイグレーション中という。

■オブジェクト指向のRubyに、数式処理ソフトウェアMathematicaの機能を自然な形で取り入れてみよう!?　

　「Rubyで数独ソルバを書いてみる」でMathematicaで書かれたコードをRubyに翻訳してみました。その作業をしながら考えたことは、「Mathematicaの機能をRubyに自然に取り込むとしたら、一体どういう言語仕様になるのだろうか」ということです。すべてのものが「リスト」であり、基本的に関数型言語であるMathematicaの機能を、多くのものを「オブジェクト」として扱うオブジェクト指向のRubyに（Rubyになじんだやり方で）取り入れるとしたら、一体どんな記述になるのだろう？という疑問です。

　RubyとMathematicaを繋いだものとして、Ruby/Mathematicaがあります。Ruby/Mathematicaで「Cos(x)をxで積分した結果」を求めるコードは下のようになります。

math=Mathematica::Mathematica.new.start
puts math.eval_foreground('Integrate[Cos[x], x]')

　このコードは'Sin[x]'を出力しますが、「オブジェクト指向」のRubyに溶け込んでいるとは言えない記述になっています。

　そこで、頭の整理がてら、もしもMathematicaのコードをRubyに溶け込ませるとしたらどうなるかを考えながら、「Mathematicaの機能を(.NETベースの)IronRubyに取り込むコード」をつらつら書いてみました。

　書いたコード（ライブラリ）は後述することとして、まずは、そのコードを使った例を紹介してみることにします。たとえば、「Cos(x)をxで積分した結果」を求めるなら、こんな感じの記述になります。

p 'x'.Cos.Integrate 'x'

これは、'xという文字列オブジェクトにCosメソッドを適用し、さらに"x"で積分するというメッセージを投げる、という具合の記述です。コードをそのまま読んでいくなら、「'x'のコサイン関数をxで積分する」という具合になります。

　あるいは、'2 x + 3 == 0'という方程式を、xについて解くなら、

'2 x + 3 == 0'.Solve 'x'

という具合の記述になります。何だか、少し「Rubyみたいな」コードに見えてくるのではないでしょうか？

　同様に、「（Rubyネイティブの!）配列"[[1,2,3],2,3]"について、それぞれのサイン関数を求め、数値化する（その結果を出力する）コード」なら、こんな具合です。

p ([[1,2,3],2,3]).map.Sin.N

　ここで、"map"はRubyのメソッドで、"Sin"と"N"はMathematicaの関数です。RubyのメソッドとMathematicaの関数が入り混じっていることがわかります。それらは、頭文字が大文字なのがMathematicaの関数で、頭文字が小文字なのがRubyの関数ということで区別することができます。RubyとMathematicaでは命名規則が異なるので、名前がぶつかることはありません。 　ちなみに、

p 3.Times(10).Plus 5

というコードを書けば、これは「3に10を乗算した結果に5を足した結果を出力する」ということになります。この"Times"も"Plus"も、あたかもRubyっぽく見えますが、いずれもMathematicaの機能（関数）です。

　さて、オブジェクト指向のRubyにMathematicaの機能を自然な形で取り入れるために、試しに書いてみたコードは、下のようになります。

　…下のコードを要約すると、メソッド名が見つからない場合に呼ばれるmethod_missingで、「見つからないメソッドがあった場合には、その命令をMathematicaに投げちゃえ」というだけのコードです。つまりは、単に(Ruby上で)未知のメソッドを「右(Ruby)から左(Mathematica)に受け流す」という「ムーディ勝山」方式…ということになります。しかも、オブジェクトの総本山、Objectクラスにその「ムーディ勝山」メソッドをいきなりMix-inしてしまう…という、とんでもないコードです。一発ネタ的コードとして、楽しんで頂けたら幸いです。

# 2010/05/12 jun hirabayashi jun@hirax.net

class Mathematica
  require 'Wolfram.NETLink'
  include Wolfram::NETLink
  # ここにMathKernel.exeへのパスを記述する
  PAR="-linkmode launch -linkname 'C:...\\MathKernel.exe'"

  def Mathematica.to_m(array)
    strArray=[]
    array.each do |item|
      if item.kind_of? Array
	strArray＜＜Mathematica.to_m(item) 
      else
	if item.kind_of? String
	  strArray＜＜'"'+item+'"'
	else
	  strArray＜＜item
	end
      end
    end
    '{'+strArray.join(',')+'}'
  end
  
  def Mathematica.to_a str
    require "JSONParser" 
    jsonParser=JSONParser.new
    s=str.gsub(/, ([^{]{1})/,',"\1')
    s=s.gsub(/([^}]{1}),/,'\1",')
    s.gsub!(/\{([^{]{1})/,'["\1')
    s.gsub!(/([^}]{1})\}/,'\1"]')
    jsonParser.parse s    
  end

  def Mathematica.callback
    proc {
      @kernelLink.EvaluateToInputForm 'MVClose[]',0
    }
  end

  def initialize()    
    ObjectSpace.define_finalizer self,Mathematica.callback
    @kernelLink=MathLinkFactory.CreateKernelLink PAR
    @kernelLink.WaitAndDiscardAnswer
  end
  
  def do(q)
     @kernelLink.EvaluateToInputForm q,0
  end
  
end

module MathematicaModule
  def method_missing(name, *args)
    $mathematica=Mathematica.new unless $mathematica
    if self.kind_of? Array
      obj=Mathematica.to_m(self) 
    else
      obj=self 
    end 
    if name.to_s
      results=$mathematica.do( [name,'[',
          ([obj]+args).join(','),']'].join('') )  
    end
    return results
  end

  def To_a
    Mathematica.to_a self
  end
end

class Object
  include MathematicaModule
end