2013-01-24[n年前へ]
■シュワルツネッガー・ファインマン…あの有名人(の顔)曲線を、検索エンジンWolfram Alphaで描いてみよう! 
 数式処理ソフトMathematicaの開発元であるWolframが提供している検索エンジンWolfram Alphaでは、「有名人(の顔)曲線」を眺めることができます。たとえば、
Albert Einstein curveと検索すると、アルバート・アインシュタインの顔をパラメータ曲線として描いたグラフ画像を眺めることができます。
数式処理ソフトMathematicaの開発元であるWolframが提供している検索エンジンWolfram Alphaでは、「有名人(の顔)曲線」を眺めることができます。たとえば、
Albert Einstein curveと検索すると、アルバート・アインシュタインの顔をパラメータ曲線として描いたグラフ画像を眺めることができます。
今日は、そんな「有名人(の顔)曲線」の一覧を作ってみました。どの顔が「誰であるか」がわかるでしょうか?あるいは、どこかに隠れているはずの「アーノルド・シュワルツネッガー」を見つけ出すことができるでしょうか?

ちなみに、登場している人(曲線)たちは、Justin Bieber-like curve,Silvio Berlusconi curve,Wolf Blitzer curve,Charlie Chaplin curve,Anderson Cooper curve,Tom Cruise curve,Dalai Lama curve,Ellen DeGeneres curve,Paul Adrien Maurice Dirac curve,Albert Einstein curve,Richard Feynman curve,Bill Gates curve,Goethe curve,Che Guevara curve,Adolf Hitler curve,Angelina Jolie curve,Kim Jong Un curve,Lady Gaga curve,Jay Leno-like curve,David Letterman curve,Abraham Lincoln curve, curve,Marx-Engels-Lenin curve,Angela Merkel curve,Barack Obama curve,Barack Obama (with hair) curve,Conan O'Brien curve,PSY curve,Vlamidir Putin curve,Srinivas Ramanujan curve,Mitt Romney curve,Arnold Schwarzenegger curve,Josef Stalin curve,Stephen Wolfram curve,Howard Stern curve,John von Neumann curve,Oprah Winfrey curveといった具合です。そして、この画像群を作るためのMathematicaコードは
list = WolframAlpha["Person curve", "Result"];
result = Table[
a = (WolframAlpha[#, "PodCells"][[2]]) &@
(list[[#]]) & @@ {i};
Export["temp.jpg", a];
ImageCrop[Image@Import["temp.jpg"],
{210, 210}, {Right, Bottom}]
, {i, 1, Length@list}]
といった具合です。
2013-02-16[n年前へ]
■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ 
 数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
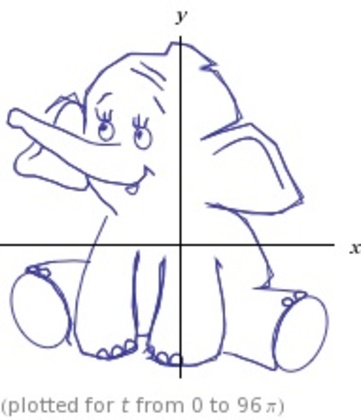
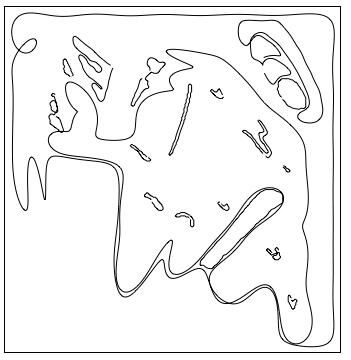
「ゾウさん曲線」あるいは
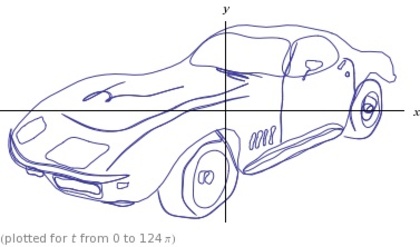
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?
数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
「ゾウさん曲線」あるいは
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?

実は、こういった「画像を表現するパラメータ曲線(群)」は、(かなりの部分を)自動的な作業により、比較的簡単に作り出すことができます。
それはこのような手順です。

- (通常画像から自動生成する場合)画像を白黒濃淡(グレー)画像にして、(少し画像をぼかした上で)濃淡値の等高線を作る
- (通常画像から自動生成する場合)各等高線は(画像境界部などの例外を除けば)閉曲線になっているので(等高線が途切れたりすることはないですから)、各閉曲線をフーリエ記述子で表現する
- (イラストから生成する場合)複数曲線からなるイラストを作り、各曲線をフーリエ記述子で表現する
- 各曲線を表現するフーリエ記述子の低次の項(低次の3角関数)だけ抜き出し、リストにする(並べる)
- …それらのパラメータ曲線群を並べたもの=任意の図形を描き出す曲線の集合になる
 「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
そして、そんな(単純のために閉曲線であるとします)閉曲線を描き出す(1周するごとに周期関数となる)パラメータの動きをフーリエ変換することができますから、結局のところ3角関数を重ね合わせたものをパラメータにして表現される曲線として、任意の(閉)曲線を表すことができる…というわけです。これが図形のフーリエ記述子による表現です。
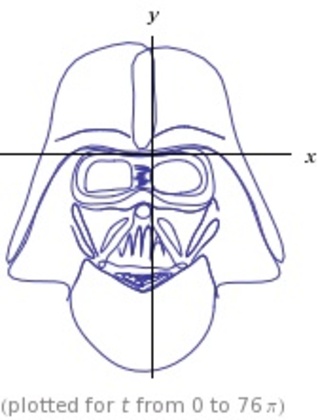 さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
これがWolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピです。…作り方を眺めてみれば、あまり「意味や価値・美しさのない曲線(存在)」に思えてしまうかもしれませんね。
2013-05-01[n年前へ]
■「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密 
 「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密を書きました。
「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密を書きました。
実は、こうした曲線数式は、「フーリエ記述子」という技法を使って自動・単純作業から簡単に作り出すことができるものです。ちなみに、「フーリエ記述子」というのは、たとえば次のようなテクニックです。
…これらが、知識検索エンジンWolfram Alphaが作り出す「さまざまな曲線数式」の作りテクニックの秘密です。…実際、「表示されている曲線を示す数式」を眺めてみれば、「三角関数の足し合わせ」で表されていることがわかります(つまり、数学的には、実際のところ、それほど美しいものではありません)。
2013-06-17[n年前へ]
■検索エンジン Wolfram Alpha が作り・表示する各種の「曲線」の裏側 
 検索エンジン Wolfram Alpha が作り・表示する各種の「曲線」の裏側が、
WOLFRAM BLOG で Making Formulas… for Everything—From Pi to the Pink Panther to Sir Isaac Newton として詳しく解説されています。(参考:「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密・Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ)
検索エンジン Wolfram Alpha が作り・表示する各種の「曲線」の裏側が、
WOLFRAM BLOG で Making Formulas… for Everything—From Pi to the Pink Panther to Sir Isaac Newton として詳しく解説されています。(参考:「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密・Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ)
かなりボリューム満点な記事ですが、実際に動かすこともできるWolfram CDF Player 用ファイル(MakingCurves_blog.cdf)もあるので、フーリエ記述子で描かれた世界を実感しつつ・楽しむことができるかも。
2013-06-23[n年前へ]
■”賭博黙示録カイジ”の顔数式曲線…それは、人間、いや生物の進化・退化の歴史だった!? 
 ”賭博黙示録カイジ”の顔数式曲線…それは、人間、いや生物の進化・退化の歴史だった!?を書きました。
”賭博黙示録カイジ”の顔数式曲線…それは、人間、いや生物の進化・退化の歴史だった!?を書きました。
…こんな風に、マンガの図柄を数式で表された曲線にしてみると、マンガ化の絵柄の違いがわかって面白いかもしれません。たとえば、カイジは180次まで必要だけど、丸っこい絵柄の手塚治虫は10次までで十分だとか、ドラえもんは3次で十分だけど、スネ夫は(特に頭部は)80次の高次の項まで必要だとか…そんなマンガ図柄の特徴が見えてくるかも?…しれませんね。