2004-06-19[n年前へ]
■無限のポテンシャルと有限の時間 
人の可能性や能力は無限にあるの。だけど、人には有限の時間しかないの。これって、面白いパラドクスだと思わない?J.P.ホーガン
運動量は加えられた力積で変化する。力積は「力」×「時間」で定義される。人が持つ潜在的な力・ポテンシャルは無限、だけど時間は有限だとしたら、その結果となる人の運動量は、無限×有限=…?
■We see your potential 
子供達が学んでいく姿が見えます。夢が現実になっていくのが見えます。私たちには見えます。小さな彼らの、大きな夢が。あなたの中にある無限の可能性が見えます。「ポテンシャルって何?」とたまに訊かれる。「すぐには見えるものじゃないけれども、何かが潜在的に持っている力、みたいな感じ」と答えることが多いような気がする。そして、「その見えないものを見えるようにするのが電子写真」と答えることが多いような気もする。そんなことを思い出すマイクロソフトのコマーシャル。冒頭の音楽も映像もナレーションも大好きなコマーシャル。「今は見えないかもしれないもの、だけど、あなたが持っている可能性と未来」が見える、というコマーシャル。
ピアノが奏でる音楽を聴きながら今回のCMを眺めたり、ギターの弦の音を聴きながら、これまでのCMで、一人のお母さんの背中のたなびくマントや、ギターを弾く青年をいつかとりまく大観衆や、そして、年老いたウェイトレスが近い未来に大学を卒業していく姿を、そんな景色を眺めてみるのも気持ちが良いかも。

2005-02-11[n年前へ]
■津波研研究報告 
「津波防災アンケートを対象としたテキストマイニング手法」「危険度ポテンシャルを導入した津波避難シミュレーション」「住民意識・行動を考慮した津波避難シミュレーションモデル」などなど、なかなか興味を惹かれるような「津波研研究報告 土木学会東北支部講演概要」
2005-07-26[n年前へ]
■測地系のズレと地震グラグラ 
 「日本測地系と世界測地系のズレ」の話を読み、先日の渋谷で揺れの大きい地震に驚き、学生時代に学んだ内容を思い出した。それは、第二次世界大戦前にあった同じような「二つの測地系のズレ」の話である
「日本測地系と世界測地系のズレ」の話を読み、先日の渋谷で揺れの大きい地震に驚き、学生時代に学んだ内容を思い出した。それは、第二次世界大戦前にあった同じような「二つの測地系のズレ」の話である
 第二次世界大戦前、東京を原点とする日本の測地座標系と長春を原点とする旧満州の測地座標系が結合された時にも同様の「二つの測地系のズレ」問題が発生した。これは、東京原点付近の地殻構造が複雑でジオイドが「地球全体に適合する楕円体」に対して傾斜しているからである。(各原点の位置計測精度によるズレによるものでなく)各原点のジオイド形状の違いにより、その問題が生じた。
第二次世界大戦前、東京を原点とする日本の測地座標系と長春を原点とする旧満州の測地座標系が結合された時にも同様の「二つの測地系のズレ」問題が発生した。これは、東京原点付近の地殻構造が複雑でジオイドが「地球全体に適合する楕円体」に対して傾斜しているからである。(各原点の位置計測精度によるズレによるものでなく)各原点のジオイド形状の違いにより、その問題が生じた。
 測地系で用いられる準拠楕円体は、「原点におけるジオイド」に接する「ベッセル楕円体」として定められる。ジオイドとは「重力の等ポテンシャル面のうち平均海面と一致するもの」である。地形形状や地面内部の物質分布などにより、滑らかではあるが決して単純な形状ではない。特に、東京原点付近のような地殻構造が複雑な地域では複雑に凹凸を持つことになる。
測地系で用いられる準拠楕円体は、「原点におけるジオイド」に接する「ベッセル楕円体」として定められる。ジオイドとは「重力の等ポテンシャル面のうち平均海面と一致するもの」である。地形形状や地面内部の物質分布などにより、滑らかではあるが決して単純な形状ではない。特に、東京原点付近のような地殻構造が複雑な地域では複雑に凹凸を持つことになる。
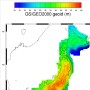 そのため、(ジオイドが凹凸形状をした)東京を原点とする日本のベッセル楕円体と「地球全体に適合する楕円体」は中心位置が大きくずれたものとなる。それに対して、(大陸内部に位置しジオイドの傾斜量が小さい)長春を原点とするベッセル楕円体と「地球全体に適合する楕円体」のズレは比較的小さい。その結果、東京を原点とする日本測地座標系と長春原点の旧満州測地座標系の間にズレが生じたわけである。
そのため、(ジオイドが凹凸形状をした)東京を原点とする日本のベッセル楕円体と「地球全体に適合する楕円体」は中心位置が大きくずれたものとなる。それに対して、(大陸内部に位置しジオイドの傾斜量が小さい)長春を原点とするベッセル楕円体と「地球全体に適合する楕円体」のズレは比較的小さい。その結果、東京を原点とする日本測地座標系と長春原点の旧満州測地座標系の間にズレが生じたわけである。
最近巷で見かける「日本測地系と世界測地系のズレ」も原因を辿れば、東京原点付近の地殻内部構造に端を発していることになる。つまり、結局のところ、日本で頻発する地震とその原因は同じであるということになる。測地系の位置ズレ問題とプレートの位置ズレ問題(地震)は似たような話、と言うことができるかもしれない。
2008-07-21[n年前へ]
■エクセルでシミュレーション Vol.4 [定常理想流体準備 編] 
夏の午後の空に浮かぶ雷雲を見ながら、昨日は静電界シミュレーションをマイクロソフト・エクセルで手軽にしてみまたわけです。暑い夏空をシミュレーションしてみたので、今度は、冷えた湧水が地下で流れているを眺めてみたくなりました。そんなシミュレーション計算をするために、理想流体の「定常的な流れ場」を表計算ソフトで解くための前準備を、今日はしてみました。
というわけで、そのためのラクガキが下の画像になります。

ここまでくると、もう「エクセルでシミュレーション Vol.1 [静電界準備 編]」と同じです。ポワソン方程式とラプラス方程式は、端的に言ってしまえばほとんど同じなので、後は「2次元の(ポテンシャル)流れ場を記述するラプラス方程式を、(エクセルの)セル間の計算式で解く」ことができることになります。
