hirax.net::Keywords::「入門」のブログ

■Spectrum Color Conversion　

　Spectrum Color Conversion は分光的な色変換を行うことができるWEBページです。 Spectrum Color Conversion::RGBtoCMY はディスプレイで用いられているような赤・緑・青のRGB加算混色で示された色（スペクトル）を、印刷などで用いられているシアン・マゼンダ・イエローのCMY減算混色で表現された色（スペクトル）へと変換します。その逆に、CMYからRGBへの変換を行うのが、Spectrum Color Conversion::CMYtoRGB です。各色に対する入力値は、RGBtoCMY・CMYtoRGBのいずれの場合も、0から255までの値を入れるようになっています。なお、CMYtoRGB の際のD65という欄には、255という数値が入っていますが、これは減算混色時にインクを照らす照明光の明るさです。この数値を変える必要は特にありませんが、もしも、この照明光D65の強度を変えたりしてみれば、その強度に応じて明るくなったり・暗くなったりすることは確認できると思います。

　CMY<=>RGB の色変換の際に用いている基準は、「スペクトル強度の差の自乗和が最小になること」です。つまり、人の視覚特性などに特化した色変換ではなく、単純に分光強度の形状が近くなるような色変換を行っています。また、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルは非常に大雑把な値を使っています。特に、シアン・マゼンダ・イエローに関しては、印刷で用いられているインクとは異なり、比較的理想に近い吸収スペクトルの場合を示しています。もしも、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルを眺めてみたい場合には、RGBtoCMYやCMYtoRGBの入力値として、単色だけを255にして、それ以外の色を0にしてみて下さい。たとえばシアンだけがある場合の単色スペクトルを眺めたければ、シアン=255, マゼンダ=0、イエロー=0にする、という具合です。すると、その色だけを使った時のスペクトルを見ることができるわけです。ただし、減産混色の場合に表示されるのは、いわゆる吸収スペクトルではなく、インクに吸収されなかったスペクトルということになります。また、CMYが示している量には対数変換がかけられています。

　RGBtoCMYとCMYtoRGBは、相互に入力スペクトルと再現されたスペクトルを比較することもできますから、RGBとCMYの間で相互に色変換を繰り返しながらスペクトルの変化を眺めてみるのも面白いかもしれません。

　なお、このSpectrum Color Conversion は、離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージをWolfram Technology 社のMathematica上で作成し、webMathematica エンジンを用いることで、web アプリケーションとして動作しています。

• 分光画像処理入門
• 応用Mathematica

■「無名関数」と「吾輩は猫である」　

　夏目漱石の「吾輩は猫である」は、雑誌「ホトトギス」に1905年1月に発表された。最初は、冒頭の章だけで完結する短い読み切り小説だった。

　吾輩は猫である。名前はまだ無い。　…吾輩がこの家へ住み込んだ当時は、主人以外のものにははなはだ不人望であった。どこへ行っても跳ね付けられて相手にしてくれ手がなかった。いかに珍重されなかったかは、今日に至るまで名前さえつけてくれないのでもわかる。

　「吾輩は猫である」を連想したのは、Mathematicaの「純関数」の勉強のための練習題材を書いていたときだ。Mathematica の入門・中級の講習会に参加すると、この純関数とやらが登場した途端に、講師が話す内容を見失ってしまうことが多い。講師の筋道が見えなくなってしまう理由は、純関数の必要性・存在価値といったものが今ひとつわからないままに、純関数がいきなり登場してくるからである。もちろん、「（数値でなく）関数を引数として与える」ということに慣れていない生徒が多いこともあって、いつも、純関数が登場した瞬間に、何かその場が失速したような感覚を受ける。

　話の流れ・必然性がなくても、文法をただ暗記することができる人であれば、おそらく何の問題もないのだと思う。あるいは、他のプログラミング言語をよく知っていて、文法の必然性が自然と理解できる人たちであったなら、これもまた問題は起きないのだろうと思う。しかし、私も含めて、入門・中級の講習会に来ているような、そうでない多くの人たちの場合は、純関数が登場した途端に、話についていけなくなることが多いように感じるのである。

　Mathematica における純関数 "Pure Function" というのは名前(シンボル)を持たない関数で、ほかの関数への引数などとして、関数の内容を書いた一瞬だけ使われるものだ。もう少し違う呼び方をしてしまえば、つまりそれは「無名関数」だ。「無名」というところが重要で、名前がないから、使ったら最後もう二度と呼ぶ・使うことはできない、ということである。つまりは、「使い捨ての関数」だ。この「関数を使い捨てる」というところで、どうしても引っかかってしまう。値を入力するのであれば、あまり考えることなどせずに、数字キーを2・3回押せばすむ。だから、値に名前（シンボル）と付けずに、使い捨てにすることには慣れている。けれど、関数を書く場合には、（ハッカーでない私たちは）頭も多少使わざるをえない。すると、せっかく考えて・苦労して書いたのだから、名前をつけて、あとで呼んでまた使うことができるようにしたい、などと思ってしまうのである。使い捨ての「無名」ということと、苦労をともなう「関数」ということを、なかなか重ね合わせることができないのである。

　そこで、自分なりの「純関数の存在価値・意義」を作ることで、その存在意義を納得したくて、純関数を使った例題を作ってみた。実は、それが前回の Spectrum Color Conversion を動かしているベース部分、「離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージ」である。これは、無名関数（純関数）を使うための例題である。このパッケージを使うと、スペクトルを描くのに、

plotSpector[ (128 red[#] + 255 blue[#])& ];

(128 red[#] + 255 blue[#])&

rgb=fitSpector[(D65[#]-128 cyan[#])&,red,green,blue]

　こんな例題を作ることで、無名関数アレルギーが低減した、と言いたいところなのだけれど、関数を使い捨てることには、やはりまだ慣れることができそうにない。関数を引数として渡すことは自然に感じられるようになっても、無名関数に名前をつけて、再度その関数を呼んでみたい気持ちはなかなか止められそうにない。名前をつけるより、その関数の中身をそのまま書いた方がわかりやすいとわかっていても、単純な名前をつけてしまいたくなる欲望はなかなか止められそうにない。

　その理由を考えてみると、やはり、苦労をともなう「関数」を使い捨ての「無名」にしてしまう、ということに一因がある。そして、もう一つ、名前をつけることで、単純化して安心してしまいたくなる、ということがあるように思う。ほんの何文字かの関数であっても、その内容を自分の頭で考えるよりは、なにがしかの単純な言葉で表現された関数名を聞いて納得したくなることがあるように思う。

　「吾輩は猫である」の第一章の最後、つまり、当初の読み切り短編小説「吾輩は猫である」はこのように結ばれる。

　吾輩は御馳走も食わないから別段 肥りもしないが、まずまず健康でびっこにもならずにその日その日を暮している。鼠は決して取らない。おさんは未だに嫌いである。名前はまだつけてくれないが、欲をいっても際限がないから生涯この教師の家で無名の猫で終るつもりだ。

■「点字」というエンコーディング　

　エレベータに乗ると、階数が描かれたボタンには、必ず点字でも階数が刻まれている。いたる所に、当たり前のように、点字が刻まれたものがある。けれど、その読み方を知っている人は決して多くない、と思う。少なくとも、私は知らなかった。

　点字印刷機のパンフレットに、点字で五十音やアルファベットや数字などが羅列してあった。そのたくさんの点字を見ていると、そこには明らかなルールがあることが見て取れる。点字は、とてもわかりやすい「決まり」で表されている。

UTF-8,EUC, ShiftJIS…そんな文字コードに触れたことがある人であれば、「点字」というエンコーディングを眺めてみると、きっと全ての人がとても面白く感じると思う。たとえば、とほほの点字入門を見れば、その面白さがわかると思う。そう、あの「とほほ」氏だって、その点字の面白さにハマっているのである。

　「点字」というエンコーディングを眺めたとき、きっと「あぁ、こんなことができるかも」と何か新しいアイデアを思いつき・実現できる人は多いと思う。そして、もしかしたら、そんな風にして実現されたアイデアの幾ばくかは何かの形となって残っていくかもしれない、とも思う。「点字」というエンコーディングは面白いと思う。

■ニッチなニッチな個人サーバ構成を図解する　

　下の図は、「ニッチなニッチな個人サーバ」の構成を図解になります。何が「ニッチなニッチ」かというと、個人でサーバを動かしていて・ソフトウェアやネットワークとはほぼ無縁の生活をしていて(何しろApacheの綴りをすべてApachと間違えて書いているくらいです)・それでいて、コンテンツ提供のサーバソフトを自分でいじったりしている・・・という状況を、とりあえず「ニッチ」としてみたのです。

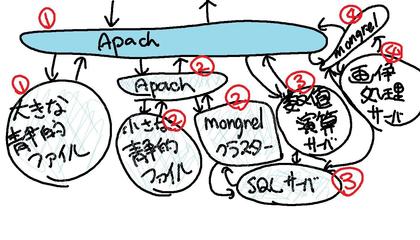
　hirax.netは現状4台のサーバで動いています。「大容量ファイル配信」「小さな静的ファイル配信」「メインコンテンツ配信用のRailsアプリを動かす mongrelクラスタ」「いくつかの実験サービスを動かすRails アプリを動かすmongrelクラスタ」「SQLサーバ」「各種数値演算用サーバ」「画像処理サーバ」といったもを、それぞれのPCに役割分散することで動いています。役割分散させると管理が面倒なので、いずれは、まったく同じ機能・同じ構成の仮想サーバにでも処理を分散させるようにしたいのですが、なかなか、そんな再構築作業ができないでいます。

　そもそも、「ニッチなニッチな個人サーバ」ですから、そんな増改築は本来必要でないように思いますが、遊びがてら色々増改築を繰り返してきた結果、こんな古い温泉街の老舗ホテルのような、あるいは、四国かどこかにあるという「軍艦島マンション」のような入り組んだ手作りサーバ構成になってしまいました。

　「Rails入門書を読んだ勢いで、個人サーバ用のアプリをRailsで書いて、自アプリでサーバ運用する人」も少なくないだろう、と思います。便利なブログツールやサーバもたくさんあるわけですが、（素人ながらも）自分で何か作ってみたくなり、適当に動かしている人もチラホラいるだろう、と思います。そんな「素人が手軽に動かすことができるお手軽・気軽なサーバ構成」は、一体どういうものなんでしょうか。他の方々のサーバは「軍艦島マンション」構成にはなってはいないものなのでしょうか……。

■中谷巌「入門マクロ経済学 第三版」　

　「入門　経済学」といった本の読みあさったので、次はもう少し詳しい本を読んでみることにした。そこで、選んだ一冊目が、中谷巌　「入門マクロ経済学 第三版」だ。「少し詳しい」と言っても、やはり選んだのは「入門本」なのである。

　今出ている第五版のことはわからないが、この本（第三版）を読んで一番良いなと思ったのが、数式にも、図にも数値が入っていることが多い、ということだ。「練習問題があって、離れた頁に数字が入っている」というわけでなく、教科書の文章中に数式と数字を同時に見ることができ、あるいは、お金の循環を示す図にも数字が入っていて、その収支をイメージだけでなく、数字で納得することができる。

　わかっているか、それとも、わかっていないかが、数字の収支を眺めてみると、あるいは違う例を頭の中で考えてみると、自動的にわかる。だから、納得することができる。

　歴史上、バブルは何回もありました。イギリスで起こった南海泡沫事件、米国における192o年代の株式ブームなど、回顧すると「なぜ？」と思われるような異様な事件が繰り返し発生しているのです。南海泡沫事件にはあの偉大な物理学者ニュートンさえ、南海会社に手をだして、多大の損失を蒙ったということですから、・・・・

中谷巌　「入門マクロ経済学」

　この本を読みながら、同時に同氏 中谷巌氏の著書を紹介する「なぜ私は変節したか？、市場原理主義の急先鋒だった中谷巌氏」という記事を読む。