1998-12-17[n年前へ]
■TuboLinux3.0でIPマスカレード 
CATVでインターネット
インストールしたPCの情報は以下の通り。
- GraphicBoard DiamondStealth3D 2000 (S3 Virge)
- EtherCard Corega PCI-T
http://blade.nagaokaut.ac.jp/cgi-bin/scat.rb/~poffice/news/fj.os.linux/15328
http://www.lares.dti.ne.jp/~gaako/linux_12.html
http://cesdis.gsfc.nasa.gov/linux/drivers/ne2k-pci.html
に辿り着く。結局、NE2000-PCI互換のボードとして認識できるようである。
ところが、TurboLinux3.0を近所の本屋で買ってしまった。これなら、CoregaPCI-Tの認識は自動的に終了してしまう。フキ出版 前原輝雄著の「新版Linuxでインターネット」と
http://www.fureai.or.jp/~fukiage/
の「TurboLinuxでのIPマスカレードのインストール」を参考に設定する。
/etc/rc.d/rc.localでmodprobeを使ってIPマスカレードを組み込む。
modprobe ip_masq_quake
modprobe ip_masq_Vdolive
modprobe ip_masq_cuseeme
modprobe ip_masq_raudio
modprobe ip_masq_irc
modprobe ip_masq_ftp
を/etc/rc.d/rc.localに追加する。
そして、ipfwadmを実行するスクリプトファイルを作成する。/home/sbin/にipmasqというスクリプトファイルを作る。
以下がその内容である。
#!/bin/sh
case "$1" in
start)
/sbin/ipfwadm -F -a m -S 192.168.1.0/24 -D 0.0.0.0/0
/sbin/ipfwadm -F -p deny
/sbin/ipfwadm -I -p accept
/sbin/ipfwadm -O -p accept
echo "Firewall & masquarading rules set"
;;
stop)
/sbin/ipfwadm -F -f
/sbin/ipfwadm -I -f
/sbin/ipfwadm -O -f
;;
*)
echo "Usage:ipmasq {start|stop}"
exit 1
esac
exit 0
そして、
chmod u+x /home/sbin/ipmasq
としておく。
これで
/home/sbin/ipmasq start
でスタート
/home/sbin/ipmasq stop
でストップできる筈だった。
しかし、何故かうまくいかない。ところが、linux-mailinglistで同じ問題が議論されていた。そこで、その中でまとめられていた対策を行う。
cat /proc/sys/net/ipv4/ip_forward
をすると、0という結果になる。これが、まずいというので、
echo 1 > /proc/sys/net/ipv4/ip_forward
で1にしてやる。すると、何の問題もなく動くようになる。
結局、/etc/rc.d/rc.localに
#dynamic ip-adress enable
echo 1 > /proc/sys/net/ipv4/ip_forward
を記述する。
Windows95/98マシンの方では、GatewayのアドレスとしてにLinuxボックスの内部IPアドレスを指定する。
1999-01-30[n年前へ]
■渡り鳥の秘密 
3000kmの彼方へ
先日、福島のいわき市の近くに友人を訪ねた。その近くで、はるか海を渡ってきた白鳥の群れを見た。そこでどこから来るのかとか、どうやって来るのかなどの話をした。大体、以下のような疑問である。
- Q.1:海を渡るのにどの位の時間がかかるのか?
- Q.2:位置(あるいは方向)はどのように認識するのか?
- Q.3:どこから来るのか?
- Q.4:なぜ渡るのか?
Q.3のどこから来るのかについては、仙台市科学館の中のGooseSchool(http://www.smus.city.sendai.jp/goose/home.html)に簡単な説明があった。そこにガンの「渡り」の地図が示してあった。その図を引用させて頂く。いや、もちろん「白鳥でなくガンであるし、そもそも飛んでくる場所が違う」のはわかっている。しかし、先の疑問の「どこから来るのか」はべつにいわき周辺の白鳥にこだわった疑問ではないのだから、他の場所の他の動物でもいいのだ。
 |
さて、残る疑問は、
- Q.1: 海を渡るのにどの位の時間がかかるのか?
- Q.2: 位置(あるいは方向)はどのように認識するのか?
このGooseSchool(http://www.smus.city.sendai.jp/goose/home.html)には「渡り」をどのように行うかという簡単な説明がある。それによれば、
- A.1: 人工衛星用位置送信機を取り付け経路を追跡した結果では2日間で2000kmをノンストップで渡り続ける。
- A.2: 時間は体内時計で知り,方向は星や太陽で分かる。鳥はコンパスや六分儀のような能力を両方持っている。
そこで、簡単に手に入った
- 「鳥の渡りの謎」 (ロビン・ベーカー著 網野ゆき子訳 平凡社発行 ISBN4-582-52717-5)
- 「鳥学の世界へようこそ」 (ディヴィッド・ラック著 蓮尾純子 訳 平河出版社ISBN4-89203-192-5)
「鳥の渡りの謎」の原著の表現では「渡り」を"navigation"と表現し、「鳥学の世界へようこそ」の原著の表現では"migration"と表現しているのも視点の違いとして面白い。
さて、この2冊の本はいろいろな実験を行った論文を引いて、「渡り」に関しての実証を行っている。動物が絡んだ実験は、実験の精度を高めることがなかなか困難に思えるが、そこはしょうがないだろう。というわけで、必ずしも実験が信用できるわけでもない。特に磁気に関する実験に関して精度の低さを感じる。
しかし、今回は自分で実験も解析もしていないので、簡単なまとめだけにしておく。
- 鳥(種類、地域、条件)により「渡り」の際に使用する航法(navigation)は異なる。
- 方位を頼りにするやり方も、位置を頼りにするやり方もある。使用されるのはどちらか片方のみというわけでもない。
- 位置のセンサーとしては、目印、音、におい、磁場*、重力*
- 方位のセンサーとしては、太陽の位置、光の偏光パターン、星、月などの位置、地磁気*
さて、今回は下調べばかりであった。これでは、いけない。いけない。自分で実験もしなければ意味が無い。というわけで、近日中にある実験をする予定である。
1999-03-25[n年前へ]
■電界計算をしてみたい[有限要素法編その1] 
有限と微小のパン
今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。
 |
何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。
 |
これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣 著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。
本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田 潔 著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。
次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。
このNotebookを使った計算、出力例を以下に示す。
| 平行平板電極の間に誘電体層があるモデル | 平板電極と三角柱電極の間に誘電体層があるモデル | 平板電極と円柱電極の間に誘電体層があるモデル |
 分割要素 |  分割要素 |  分割要素 |
 電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |
 半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |
Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。
- 油界 <- 電界
- 堰素 <- 要素
- 誘油 <- 誘電
- 姦み込む <- 組み込む
- 表傭 <- 表面
- 壓さ <- 高さ
- 堆心 <- 重心
- 肖似 <- 近似
- 内占 <- 内部
- 傭積 <- 面積
- 回寂 <- 回転
- 進当 <- 適当
- 懷瞰 <- 鳥瞰
中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。
1999-07-05[n年前へ]
■目に映る明るさって何ですか? 
君は天然色
前回、デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、
- カラーから白黒への変換はどうする?
- セピアカラーって一体何だ。
- セピアカラーへの変換はどうやろう?
カラーから白黒への変換はどうする? どうしよう? これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。) 例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。
 |
とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。
いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。
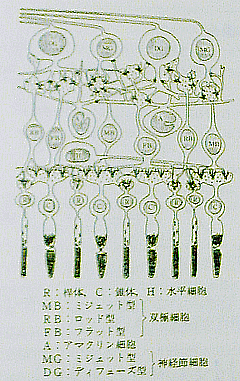 「視覚と画像」 大頭・行田 著 森北出版より |
それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。
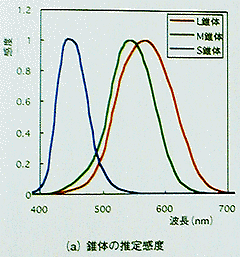 CQ出版 洪 博哲著 「お話・カラー画像処理」より |
次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。
 「視覚と画像」 大頭・行田 著 森北出版より |
後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。
というわけで、グレー化のために使っているのはこの式だ。
- Red: ptr[2]
- Green: ptr[1]
- Blue: ptr[0]、として
やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。
さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から
- 色に対する感じ方(眼とフィルム)( http://www.mmjp.or.jp/rwicp/data106.html )
- カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
- 明るさの見え方(明暗対比)( http://www.mmjp.or.jp/rwicp/data506.html )
- 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )
また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。
なお、以下のような答え方は遠慮致したい。
例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」
例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」
1999-09-17[n年前へ]
■モアレ、デバイス、2項分布の三題話 
淡色インクの副作用
今回は、9ヶ月間も寝かせた伏線にまつわる話である。いや、別に寝かせるつもりは無かったのだが、いつのまにかそんなに時間が経ってしまった。
以前、
という話があったが、その2つを結びつけるミッシングリンクについて考えてみたいと思う。「2項分布のムラについて考える(1999.01.08)」の最後に「今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、続く...」と書いた。「その続き」というわけである。始めに「2項分布のムラについて考える(1999.01.08)」の要点をまとめると以下のようになる。それは、
- ランダムと呼ばれるものの内で代表的な2項分布においては、当然のごとく「ある領域での平均値はばらつく」。
- そして、そのばらつきは直感的に考える程度よりももっとばらつく。
- 例えば、2値画像で考えるならば、2048dpi程度の解像度でランダムなデータを並べた場合には、人間の目はざらつきを感じてしまう。
そして、「モアレはデバイスに依存するか?(1998.11.20)」での要点は
- モアレにはデバイス依存性がある
- 線形な重ね合わせが成り立たない場合にはモアレが発生する。
最近のインクジェットプリンターはCMYKの4色インクだけでなく、淡色インクも使うものもある。淡色のインクを使うことで階調豊かな画像を印字できるわけだ。4色インクだけではディザなどを使って、解像度を下げて階調を出さなければならないわけであるが、それが不要になるわけだ。
解像度を下げないですむわけであるから、ディザのざらつきを感じないですむわけだ。しかし、淡色のインクを使った場合の効果というのはそれだけではないように思われる。HP(ヒューレッドパッカード)などのWEBのプリンター紹介を読んでいると、「淡色のインクを重ねて濃度を出す」というような記述を目にする。これは「少なくとも淡色インクでは線形性(あるいはそれに近い関係)が成り立つ」ということだ。
インクジェットプリンターの解像度を上げたときに、インク滴が意図しないところへずれてしまうことはきっとあるだろう。その際に他のインク滴と重なったらどうなるだろうか?意図しなくても他のインク滴との重ね合わせは発生してしまうだろう。
重ね合わせが成り立たない、非線型なインクではモアレが発生する。言いかえれば、意図しない濃度のばらつき・ざらつきが発生してしまう。「2項分布のムラについて考える(1999.01.08)」で考えたようにランダムに重ね合わさるから広い領域では一定だろうというのは予想外に成り立たないのである。でたらめというのは私の予想外に大きく効いてくるのである。
しかし、重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しないことになる。参考までにインクジェットの印字画像の拡大写真を示してみる。
 |  |
「重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しない」と、書いただけでは意図するところが伝わらないと思うので、「モアレはデバイスに依存するか?(1998.11.20)」で使った画像を用いて考えてみる。この画像は重ね合わせがある幾何学模様で生じているが、この現象がランダムに起こっているものとして読み替えて欲しい。
 |  |  |
下は、淡色のインクで重ね合わせ(インク滴の意図しない重なり)が生じた場合である。
 |  |  |
なんの模様も生じていなく、意図した通りの画像出力ができているのがわかると思う。
ということで、今回の話(というか前の2回の話)の繋がりは、
淡色のインクを用いたインクジェットプリンターでは、意図しないインク滴の重ね合わせが生じてしまっても、濃度変化が生じにくく、意図しないインク滴の重ね合わせがでたらめに発生してしまったとしても、画像にはあらわれない可能性があるということである。
うーん、マニアックな内容だ。「身近な疑問を調べる」という看板に偽り有り、である。しかも単なる推論だ。
しかし、もしもインクジェットプリンターを買う人がいるならば、淡色のインクを使っているものを購入するといいかもしれない、ということがわかっただけでも良しとしておこう。