1998-11-20[n年前へ]
■モアレはデバイスに依存するか? 
まず、以下のような2つの同心円画像をつくる。(なお、このような画像を簡単に作るために、Photoshop用のフィルターを作った。詳しくは「Photoshopの同心円フィルターを作る。」を参照して頂きたい。)以下の2つの画像は少し中心位置がずれている。また白く見えるところは255の値を持ち、黒く見えるところは0の値を持っている。(画像自体は512x512であり、表示の際に128x128に変換している。だから、この画像をそのまま保存して頂ければ、512x512のサイズで保存することができる。)
 |
 |
- 黒(0)+黒(0)=0(すなわち黒)
- 白(255)+白(255)=255(すなわち白)
- 黒(0)+白(255)=255(すなわち白)
- 画像1を白黒反転し、画像1'を作る。
- 画像2を白黒反転、画像2'を作る。
- 画像1'と画像2'を加算し、画像3を作成する。
- 画像3を白黒反転し、画像3'を作成する。
 |
それでは、以上の画像変換を小さい画像でまとめて表示してみる。
 |  |  |
ところで、上の3つの画像をそれぞれ平滑化してみる。すると、以下のようになる。
 |  |  |
以下でもう少し詳しく考えてみる。
重ね合わせにおける加算演算
下のような画像A、画像Bを考える。拡大してあるが、画像自体は1x2ピクセルのサイズである。また、白=255、黒=0とすれば、いずれも平均値は128程度である。 |  |
- 黒+黒=黒
- 白+白=白
- 黒+白=黒
 |  |  |
 |  |  |
 |  |  |
これに平均値も示すと以下のようになる。ここでは、LBPなどの紙に出力する際によく使われる、白=0、黒=255という表記をする。
 |  |  |
 |  |  |
 |  |  |
同じ128+128でも、結果は128になるか256になるかの2種類ある。同じもの同士であれば、結果は128であるし、そうでなければ256になる。そのために、平均値が保存されないのである。このように、平均値が保存されない、言い換えれば、加算演算の結果が線形でない場合にはモアレが発生することになる。もしも、マクロに見て「128+128=256」が多い領域があれば、それはモアレの黒い部分であり、そうでない所は比較的明るい部分であるということになる。
ロゲルギストの-モアレが生じる理由は黒さの非線形性による-という言葉はこの「128+128=128、と128+128=256という結果の違いがあり、それがモアレの原因である」ということを示している。
それでは、そのような現象「128+128=128という非線形性」が起きない状態を作ってみる。それには加算の結果である黒がサチらないようにすれば良い。
 |  |  |
 |  |  |
 |  |  |
これでは、いずれの状態でもグレー+グレー=黒、すなわち、64+64=128という風になっている。これは黒がサチっていないからである。すなわち、-モアレが生じる理由である黒さの非線形性さ-がない状態になっている。
それでは、この状態で計算実験Aと同じことをしてみる。それを計算実験Bとする。念のため、計算実験Aをもう一度示す。
 |  |  |
 |  |  |
 |  |  |
| 画像1の黒=0を128にした画像4を平滑化したもの | 画像2の黒=0を128にした画像5を平滑化したもの | 画像4,5を加算したもの |
モアレができていないのがわかるだろうか。これはグレー(128)+グレー(128)=256(もっと黒)で線形な関係が成り立っているからである。平均化された画像で濃度がどこも倍近くになっているのがわかると思う。
モアレのデバイス依存性
LBPではトナーが有る所、すなわち、画像が有る所はほぼ完全に影になる。例え、2枚重ねてもやはり影のままである。しかし、インクジェットならどうだろうか。OHPで使うと、黒といってもLBPに比べて薄い。1枚のOHPの黒よりも、2枚のOHPの黒を重ねた方がかなり黒い。ということは、「黒+黒=もっと黒」と同じである。したがって、OHPを重ね合わせても濃度が保存されている。すなわち、モアレが比較的に出来にくいことになる。ということは、OHPを何で作るかによってモアレの具合が変わることになる。付け加えれば、実際のOHPの場合には透過率を考えなければならない。透過率というものは単なる重ね合わせでない、具体的に言えば、加算演算でなく乗算演算である。それでも、話としては大体は同じことである。
今回はOHPの話に絞ったが、透過原稿でなく反射原稿についても同じである。むしろ、反射原稿の方が乗算演算でなく、加算演算である分、今回の話そのままである。したがって、一般的なモアレについてインク(もしくはそれに相当するもの)の加算演算の具合によって、モアレの発生具合が違うと考えられる。
また、話の単純のために白黒の話に限ったが、カラーのモアレなどについてもほぼ同じであろう。トナーとインク、また、混ざりやすいものと混ざりにくい物の違いなどでも面白い結果が出そうである。TVや液晶のようにほぼ線形の重ね合わせが成り立つであろうものと比較するのも面白そうである。
今回の話を考えている途中で、OHPの重ね合わせと干渉の共通点については、結構奥が深いような気がしてきた。そのため、別の回でもう少し詳しく考えたい。
1999-02-14[n年前へ]
■感温液晶でNotePCの発熱分布を可視化する 
熱いところで感じてみたい St.Valentine 記念
東急ハンズで実験材料をいくつか買った。その中から、感温液晶シートを使って計測を行ってみたい。
色が変わる材料というものは多い。温度により物質の色がかわる現象はサーモクロミズムと呼ばれる。光により色が変わるサングラスのような現象の場合はフォトクロミズム呼ばれる。けっこう、色々な応用を見かける。
通常の感温液晶はコレステリック(Cholesteric)効果により反射光のスペクトルが変わるため、色が変化する。
これが感温液晶シートである。よくで見かけると思う。
 |  |
さて、それでは感温液晶を使っていくつか測定を行ってみたい。まずは、NotePCの発熱分布を調べてみる。最近のNotePCはかなり熱くなるものが多い。暖かいというよりもアッチッチ状態になるものさえある。
それでは、
- Toshiba Libretto50
- Panasonic Let'sNote mini(AL-N4)
いずれも、感温液晶シートをNotePCの上に載せることにより、評価を行っている。今回は発熱分布を知ることが目的であるので定量的な評価は行っていない。もし、温度を定量的に行いたいのであれば、色と温度の対応曲線をあらかじめ測定する必要がある。
以下に結果を示す。
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 |
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 感温液晶シートのサイズがA4であるため、Let'sNote miniにちょうどフィットする。 |
Libretto50ではPCカードのNICを右に挿しているため、キーボードの右側部分の発熱が大きい。また、下面ではハードディスク部分の発熱がわかる。また、ク*ックア*プしているせいかかなりアッチッチである。
Libretto50,Let's Note miniいずれにおいても液晶のドライバーがある部分(液晶の左)は発熱が激しいのがわかる。
本来ならば、愛用しているTOSHIBA Portege320でも計測を行いたい所だが、ただいま長期入院中である。間もなく使用1年になるが、これまでに入院3回を経験し、入院期間は計2ヶ月にわたる。昔の小説家もビックリの病弱さである。他の使用者の話を聞いていても実に不安定な機種のようだ。一体、疲労骨折を経験していないPortege320というのは、はたして存在するのだろうか。あぁ...
今回は手元にあったNotePCでのみ測定を行ったが、近所の協力の下に色々なNotePCの発熱分布を調べる予定である。特にパームレスト周りの発熱分布などは割に軽んじられているだけに、興味がある。
今回は感温液晶を使った温度分布の簡単な可視化をしてみた。同じような測定は色々してみる予定である。
感温液晶と同じように、温度で変化する材料は多い。例えば、FAXでよく使用される感熱紙もそうである。
他にも、RICOHの熱可逆性情報表示フィルム
http://ext.ricoh.co.jp/saiyo/sin/prof/eyes/page4_2.html
などもそうである。
これなどはお店のポイントカードなどでよく見掛ける。私の財布から探してみると、オートバックスのポイントカードがこれと同じようなものである。70-130℃位の温度変化により透明度を変化させる材料である。これ位の温度であると、真夏の車中にカードを放置するとどうなるか心配なところである。
今回の情報に関連するWEB一覧
- 伊藤のホームページ(http://www.infonia.ne.jp/~itous/)
- 岡山県教育センター(http://www.pref.okayama.jp/kyoiku/sido/edu_cent/seminar/rika/rikasho/zikken.htm)
- お湯で変色するサーモクロミズム化合物をつくる(高橋 正)(http://www2b.biglobe.ne.jp/~murasho/news22.htm)
- 液晶について(http://www.osakac.ac.jp/labs/fujita/asai/ekisyo.html)
- 感温液晶を用いた非定常熱伝達の計測システムの基礎的研究(http://village.infoweb.ne.jp/~fwhz0564/kenkyu.htm)
- 感温液晶マイクロカプセルによる可視化(http://koneeko.linux.or.jp/AandO/gfd_exp/exp_j/tech/elc.htm)
1999-02-26[n年前へ]
■ヒトは電磁波の振動方向を見ることができるか? 
はい。ハイディンガーのブラシをご覧下さい
(1999.02.26)
リチャード・ファインマンの本の中で次のような問題があったように思う。
「偏光板がフィルターが一枚だけある。その偏光フィルターの偏光方向をどのようにして知れば良いか?」
その本の中での答えは、
「物体の反射光を偏光フィルターを通して見てみる。」
だった。ブルースター角で入射した光の反射光は、入射面に対して電場の振動方向が垂直になっている、ということを利用するわけである。
分かりやすいように、偏光フィルターを通してみたガラスの反射光をデジカメで撮影してみる。左が反射光を通すような角度に偏光フィルターを回したものであり、右が反射光をカットするような角度に偏光フィルターを回した場合である。この左の場合、すなわち、反射光が一番通過している角度から液晶の偏光面がわかるわけである。
 |  |
ところで、このようなファインマンが示したような方法を用いなくても、そもそもヒトは電磁波の振動方向を見ることができるのである。以前、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「鳥は太陽の位置、光の偏光パターンを位置のセンサーに使う」という話があった。ヒトも同じく光の偏光方向、すなわち、電磁波の振動方向を見ることができるのである。鳥はどう見えるかは私にはわからないが、ヒトならば自らが実験台になれるので、電磁波振動方向をどう見ることができるか調べてみたい。というわけで、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「近日中にある実験をする予定である」と書いたものが今回の確認実験である。なお、光の進行方向と磁界の振動方向を含む面を「偏光面」、電界の振動面を含む面を「振動面」と呼ぶ。
電磁波の振動方向をヒトが見ると「ハイディンガーのブラシ "Haidinger'sBrushes"」というものが見える。それを知ったのは、いつものごとく「物理の散歩道」からである。網膜に複屈折性があるために「ハイディンガーのブラシ」が見えるのだという。
私はこれまで、「ハイディンガーのブラシ "Haidinger's Brushes"」を見たことがない。いや、正確に言えば意識したことがない。そこで、判別しやすいように直線偏光を用意してやることにした。そこで、東急ハンズで偏光フィルターを買ってきた。
そして、空を見てみる。もちろん、偏光の偏りが強い、太陽を中心にして90度の角度をなす同心円方向である。詳しくは、
- 可視-赤外域での偏光観測による衛星観測手法の開発基礎研究(http://www.mri-jma.go.jp/Dep/sa/Lab1/labt01-s.html)
- エアロゾル観測(http://mars.im.kindai.ac.jp/KISYO/YPROJECT/kansoku.html)
さて、ヒトである私は、空を眺めて格闘すること5分程で、「ハイディンガーのブラシ"Haidinger's Brushes"」がわかるようになった。私が見たハイディンガーのブラシ"Haidinger's Brushes"を示す。
 |
この絵で太陽の方向は右上であり、偏光面は次の絵の青の矢印方向になる。
 |
というわけで、ヒト(少なくとも私は)電磁波の振動方向を見ることができるのである。慣れてしまうと、白い紙を見つめているときなども(条件によっては)見えるようになる。色を扱う人は意識すると面白いと思う。
ところで、偏光フィルターがどういうものか知らない人のために、NotePCの液晶に偏光フィルターを重ねた写真を示す。
 |  |
なぜ、こうなるかわからない方は、
などを参考にして欲しい。液晶ディスプレイの構造がわかると思う。そして、面白いことに気づいた。NotePCの液晶からの光は直線偏光である。ということは、NotePCの液晶にはハイディンガーのブラシが映っているのである。正確に言えば、NotePCの液晶を見ているあなたの視界の中央には、ハイディンガーのブラシが映っているのである。と、気づいてみると確かに見えている。
というわけで、液晶ディスプレイを使用している方はハイディンガーのブラシを見て頂きたい。以下のやり方がわかりやすいと思う。
1.このWindowを最大化する
2.下へスクロールして画面を真っ白にする。
3.液晶ディスプレイ(NotePC)を回転させる。
4.画面(視点)の中央に(視点に対して位置が)動かない黄色いもやが見えるはず。もちろん、回転はする。
液晶ディスプレイやヘッドマウントディスプレイ(HMD)を色々見てみたが、どれにもハイディンガーのブラシは存在していた。視界の中央に不思議な十字架のように現れているのである。現代の液晶技術が負う十字架である。
誰もが、目の前にあるのにそれに気づかないというのも、実に面白い。まるで、「青い鳥」のようである。そして、そういうことはとても多いのではないかと思う。それはそれで面白い話だ。
- それでは、ハイディンガーのブラシをご覧下さい -
2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
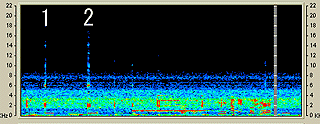 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-03-19[n年前へ]
■一家に一台、分光器 
ハサミとテープで「できるかな?」
いきなりであるが、分光器を作りたい。光を波長別に分ける機器である「分光器」である。とある実験をするために、分光器が必要なのである。その「とある実験」の影には、大きな野望があるのだが、まだ明らかにする訳にはいかない。とりあえず、色の話題を考えるときに分光器があると便利だから、という理由にしておきたい。
どうやって分光器を作るか考えてみる。普通であれば、グレーティング(回折格子)やプリズムといったものを使うことになるだろう。家の中を探してみれば、プリズムなどもあるはずなのだが、WEBで情報を探してみると面白い情報があった。
- CDを利用した分光器の製作
- ( http://www.sunfield.ne.jp/~oshima/omosiro/spec.html )
- 遮光フィルムを用いた分光器の製作(その1)
- ( http://www.asahi-net.or.jp/~DJ9K-SMZ/goods/spectre/spectre.html )
次に示すのが、HIRAX一型分光器である。ハンディ・超軽量の優れものだ。テープとハサミと去年のカレンダーを駆使し、フリーハンドで作成した、製作時間20分の大作である。どうも私の仕事はテープとハサミを駆使することが多い。それは、ハードでもソフトでも、どちらでも同じことである。出来の悪いノッポさんである。
 |
左下がスリット部になっている。中央上の折れ曲がっている部分にグレーティングが配置している。次の写真を見るとグレーティングがあるのが判ると思う。HIRAX一型分光器の内部は散乱光を防止するために、黒く塗ってある。しかし、下の写真を見れば判るように、グレーティングの周りの片側は塗り忘れてしまった。まるで、「耳なし保一」である。
 |
こちらの開口部から目で覗くなり、デジカメで撮影するなりするのだ。そうすれば、スペクトルが確認できる、というわけである。
例を示してみたい。グレーティングが曲がっているせいで、スペクトルが歪んでいるし、スリットが結構太いし、サイズのせいもあってスペクトルの分解能はそれほど高くない。しかし、結構きれいな映像を得ることができる。まずは、太陽光のスペクトルを見てみる。
 |
これはデジカメで撮影したものである。スリットが太いので確認しづらいのだが、太陽光のフラウンホーファー線(FraunhoferLine)の一つHβ吸収線が486nm(ここでは水色の中央部)辺りに見えるような気がしないだろうか? いずれ、スリット幅を小さくして、もう少し精度の高い実験をしてみる予定である。
さて、次の例は「自宅の蛍光灯のスペクトル」である。
 |
- 黄色、橙色 579、577nm
- 黄緑色 546 nm
- 水色 436 nm
- 紫色 408、405 nm
 |
目で覗いたり、デジカメで撮影したりするのも面倒なので、可視・赤外領域に感度を持つCCDボードを秋月で買ってきた。次回、このCCDボードを取り付けて見る予定だ。そして、定量化をしてみたいのである。そして、ある野望のためにせっせと実験を続けていく予定である。