hirax.net::Keywords::「反復計算」のブログ

■エクセルでシミュレーション　Vol.10　二次元非定常熱伝導問題シミュレーション＋P(ID)制御エクセルシートを作ってみよう　

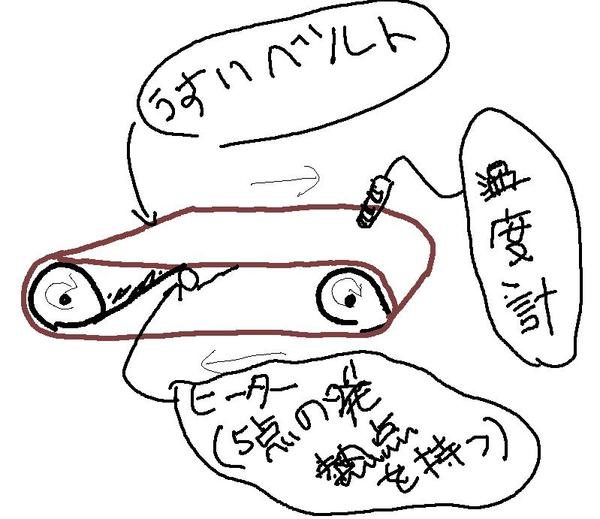　「エクセルでシミュレーション　Vol.9　二次元非定常熱伝導問題の温度変化グラフも作ってみよう」で、二次元非定常熱伝導問題を解くシートを使いながら（実用的範囲では三次元問題と大差がない）、ヒーターで回転するベルトを高温にした場合の、その回転ベルトの温度分布がどのように変化していくかを計算し、グラフ化し、さらにベルト中の一部分の温度を時系列的にモニターする機能を付けた、シートで遊んでみました。

　そこで、今回は、センシングしたベルトの温度を用いて、ヒーターの温度を簡単なPID制御を使ってフィードバック制御するエクセル・シートを作ってみることにしましょう。

PID制御とは、調整量を（現在の）出力値と目標値との差に比例＝Proportionalした量、その（過去からの）積分=Integralに応じた量、および（その瞬間に次にどのように変化するかという）微分=Differentialに応じた量にしたがって変える制御です。言いかえれば、現在（Proportional）・過去（Integral）・未来（Differential）の挙動に応じて、制御調整量を変えてやろうという制御です。比較的、古典的な制御手法ですが、現在でも、もっとも一般的な制御手法です。

　まずは、前回のエクセル・シートでヒーター部分を単純に（計算をさせ始めてから＝回転ベルトに対するヒーターを動かし始めてから）100℃にし続けた場合の計算過程を示してみます。つまり、何の制御もしない場合です。その計算結果が、下の動画です。上の動画で上に示したグラフが、回転ベルトの温度分布を示したグラフです（回転ベルトを切り開いたように温度分布を示しています）。動画中の下の折れ線グラフは（上のコンター図で灰色丸部の温度の時間変化を示したグラフです）。ちなみに、縦軸は0℃から150℃までで、横軸が時間軸です。

　下の折れ線グラフを見れば、上のコンター図で灰色丸で示した部分の、温度が時間に応じて上昇し、やがて100℃近くになっていることがわかります。

　さて、次にPID制御を行ってみることにしましょう。…とはいえ、最初は簡単のために、「灰色丸で示した部分の温度と目標調整温度である100℃との差をヒーターに足す（ネガティブ・日―ドばっく）」という「P=比例成分=現在の違い」だけを利用したP(ID)制御を行ってみます。つまり、現在の出力と目標出力の差異のみをヒーター出力に（適当な比率で）足し合わせてみるのです。言いかえれば、ベルトの温度が0℃なら、ヒーターを200℃くらいにすることで、急激にベルトを温め温度を調整し、目標温度100度と現在のベルト温度の差が小さくなってきたら、ヒーターの温度を110℃くらいに変えてやる・・・というような制御をしてみます。そんなシミュレーション計算を行ってみた結果が、下の計算結果になります。ちなみに、ヒーターの制御温度はエクセルのシートでB32セルで計算されています。また、灰色丸のセンサ取り付け部分（を示した）の温度を示す下の折れ線グラフは、先ほどと同じく、縦軸は0℃から150℃までの温度を示し、横軸が時間軸となっています。

　この結果動画を見るとわかるように、「P=比例成分=現在の違い」だけを利用したP(ID)制御（=積分成分と微分成分を使わない）制御では、ベルトの温度は早く立ち上がりますが、ベルトの温度は振動して、なかなかすぐに安定してくれません。しかも、早く温度を立ち上げようとすると、温度振動は大きくなってしまい、温度振動を防ごうとすると、なかなか温度が早く立ち上がってくれない、という相反する関係になっています。いわば、（ある程度、減衰がある）強いバネと弱いバネの振動と同じような現象が起きてしまいます。

　さて、それでは、一体どうしたら良い制御ができるのでしょうか。・・・せっかく、簡易にエクセルのような（表計算＝スプレッドシート・ソフトウェアを使った）熱伝導方程式を使ったシミュレーション計算を行うことができる環境があるわけですから、今回扱ったPID制御のような古典的な制御をもう少し復習してみようと思います。

　そして、せっかく熱伝導方程式を計算してみたりしているわけですから、そういった微分方程式（つまり現在から未来を示す式）を使うことで実現できる、最適化制御についても考えてみることにします。

■名前付きセルのあるエクセルのワークシートをC++言語プログラムに変換してみよう　

これまで「続　エクセルの計算ワークシートをRubyでC言語に変換してみよう」や「エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう」で、エクセルの表計算シートを他の言語のプログラムに変換する、なんていうことをしてきました。ここで想定している「エクセルの表計算シート」というのは、「エクセルで作った離散化シミュレーション用.xlsシート」を主眼に置いています。つまり、何らかの方程式を差分化し、エクセルシート上でその差分化された空間を表現し、反復収束計算ことで求めたい結果を得る、そんなためのエクセルシートを主眼に置いています。

　ところで、そんな風にエクセルシートを使うときには、セルに名前をつけたくなります。たとえば、真空の透磁率をA1セルに入れたら、そのセルを"A1"セルでなく、"eps"なんていう名前で参照したくなります。そこで、たとえばこんな風にセルに名前をつけます。すると、そのセルの値を、"A1"というようにも参照できるのに加えて、"eps"なんていう名前でもアクセスすることができるようになります。そうすれば、他のセルでは"=eps*4"なんていう風に数式を入力することができるわけです(参考ビデオ）。

　そこで、今回は名前付きセルを使ったエクセルのワークシート（簡単のために、一枚目のシートだけを使ったエクセルブックを前提にしています）をC++言語プログラムに変換するRubyスクリプトを書いてみました。変換用のRubyスクリプトや、名前付きセルを使った（ラプラス方程式を解く）エクセルシートや、エクセルシートから変換・作成されたC++言語ソースファイルは、ここに置いておきました。このサンプルのエクセルファイルでは、中心のセルの値を変化させるために入れるセルに"centerVal"という名前を付けています。そのため、変換されたC++ソースには、

  C3=centerVal;

names={}
book.names.each do |name|
  cell=$1.gsub('$','') if /!([^!]+)$/=~name.RefersTo
  names[cell]=name.name
end

　名前付きセルを使ったエクセルシートを使い物理定数や中間変数などをわかりやすく表現した上で、離散化シミュレーションをシート上の「いかにもわかりやすく「差分化された空間で」実感した後に、（その自分自身が作ったスプレッド・シートを元に）変数の名前が（少なくともA1とかD4とかいう名前よりは）わかりやすいシミュレーションプログラムが自動生成されるとしたら、つまり、自分自身がスプレッド・シート上で作ったものが、C++言語の（もちろん他の言語でも）プログラム・ソースとして眺めることができるとしたら、…これって結構面白いと思いません？

■続　エクセルにおける循環参照時の計算順序　

　「エクセルにおける循環参照時の計算順序」で書いたような反復計算がおこなわれるのは、あくまで「循環参照」がされているセルに対してである。この「循環参照がされているセルに対して」ということは、えてして忘れてしまいやすい。つまり、シートの一部に「循環参照」がされているセルがあれば、シート全体が反復再計算されるのだ、という勘違いをしてしまいやすいように思う。

　反復計算がされるのは、あくまで「循環参照」がされているセルだけ、である。「循環参照」がされているセル群だけが反復計算の対象になり、それらのセル群の（前回計算結果との）変化量が所定値以下になるまで、それらのセル群に対して再計算を（前回記事のような順番で）行うことになる。

　シート上で「循環参照がされていないセル」に関しては、再計算されることはなく、初回の計算時の値がそのまま使われる。だから、たとえば、どこかのセルに乱数値を返すようなものが含まれていたとしても、つまり、計算ごとに明らかに変化するようなセルが含まれていたとしても、（循環参照がされていない限りは）そのセルの値は初回の計算で決まり、変化することはない。考えてみれば、当たり前の話だが、油断するとその当たり前を忘れてしまう。

　えてして、反復計算が行われる時には、シート全体が再計算されるという勘違いが頭の中に忍び込むことがある。そして、その間違った先入観のもとに、エクセルでプロトタイピングをしたりすると、思ったような計算がされず、ラピッド・プロトタイピング、すなわち、素早くたたき台を作とうと思ったはずなのに、多量の時間を費やす羽目になってしまったりする。

　エクセルの基本的な機能だけを、しかし、その基本的な機能を深く解説した本を読んでみたい。

■エクセルで飛び出す"立体"粒子群アニメーションを作ってみよう!?　

　21世紀に入った頃から、「表計算ソフトを使って、色んなシミュレーションをしてみる」ということをしています。いつも、夏になるとそんなことをしています。だから、暑い夏が来ると、いつもエクセルの勉強を”少しだけ”します。そして、いつもエクセルを憎み、一年くらいは触りたくなくなります。…けれど、憎みと愛は裏表、というわけで、結局エクセルに触り続ける毎日です。

　さて、そんな年中行事とは関係なく、昨日は「エクセルのグラフをマウスでグリグリ動かしながら赤青メガネで飛び出す立体動画で眺めよう!?」ということをしてみました。そこで感じたのは、エクセルは三次元的に眺める価値のあるグラフはなかなか作ることができない、ということでした。

　しかし、そんな風に限界を感じるときは、そこで感じる限界は多くの場合、自分の限界そのものである、ということもよく感じます。…というわけで、今日は、エクセルで粒子挙動シミュレーションを行い、その結果をアナグリフ立体動画として表示してみることにしました。

　そこで、まずは、（反復計算を用いて）簡単な「粒子挙動シミュレーション」をエクセルで行うことができるようにしました。そして、その上で、その粒子群の動きの計算結果を位置・大きさを（適当に）透視変換をした上で、散布図（バブルチャート）として、アナグリフ立体表示できるようにしてみたのです。そうすれば、左右視差による遠近感に加え、バブルの大きさが遠近に合わせた大きさで表示されることで、自然に立体感をもって眺めることができるわけです。

　その結果を、先日、作ったアナグリフ表示アプリケーションでアナグリフ立体動画にしてみた結果が、下に張り付けた動画になります。ムービーキャプチャーはいつものようにカクカクしてしまっていますが、もちろん、本当は、とても滑らかに動いています。というわけで、今日は「エクセルで飛び出す"立体"粒子群アニメーション」を作ってみました。