2000-10-29[n年前へ]
■「しょんべん小僧」の物理学 
あともう一歩、前に出ろ
以前、- スクール水着の秘密 - 腹の部分のデカイ穴 流体力学入門編2 - (2000.08.24)
「男性にはよくある風景だけれど、女性にとっては未知のミステリアスゾーン」といってもたくさんあると思うが「男子トイレ」というものだって、女性にとっては未知のミステリアスゾーンだろう。
次の絵はよくある男子トイレの一風景だ。便器前のポジションに立つとどうしても目に入る位置にこんな内容を書いたチラシが張ってあることが多い。
「ちょっと待て、あともう一歩前に出ろ。」
 |
もし、その張り紙がなかった場合にはどうなるだろうか?その場合には、下の絵のような事故が発生してしまうのである。実際のところ、ほとんどの公衆便所で見かける風景だ。
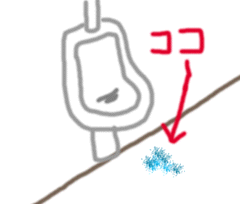 |
そう、便器にロックオンして放水をしたハズなのに、何故かターゲットである便器まで「小便」が届かずに便器下を汚してしまうのである。実にマズイ事態ではあるがよく見かける風景でもある。便器内を狙ったハズの小便が残念ながら目標地点まで辿り着かなかった場合に起きる悲劇である。
もちろん、どんなに飛距離が小さくても、すなわち小便が放水銃の先から真下に垂れてしまった場合でも、便器の顎の上から放水作業を行っていれば何の問題もないわけだ。しかし、世の中の男性達は何故か遠くから狙いたがるのである。先程の、「ちょっと待て、あともう一歩前に出ろ。」という張り紙ではないが、もう一歩前に出て便器の顎の上から放水作業を行いさえすれば良いのではあるが、何故か漢(ここではあえて、漢と書いてオトコと読むことにしよう)達はそれができないのである。
さて、この現象には別に公衆便所でなくても発生するわけで、どこのトイレでも便器の下を汚してしまうことになる。そのため、家庭によっては妻から
はるか古の昔から「男らしさ」のひとつが「立ち小便」でなかったか?、そして「立ち小便」は「男らしさ」の最後の砦ではないのか?という気も私は少しだけしたりするのだが、便器周りを汚しまくる現実の前ではそんな「男らしさ」は2000円札よりも価値がないのである。2000円札ならば喜んで受け取ってくれる人もいるだろうが、便器の下に落ちようとする「小便」は誰も受け取ってくれない。いや、実際のところ小便を喜んで受け取ってくれる人もいるのかもしれないが、少なくともそんな人の数は2000円札を喜んで受け取る人の数よりはきっと少ないだろうと思うのである。
そしてさらに、「男らしさ」が「立ち小便」なら、そんなものイラナイと言われてしまいそうな気もするし、「立ち小便」が「男らしさ」の最後の砦か!?と言われてしまいそうな気も強くするので、ここらへんについての社会学的な考察は追求しないでおこう。
それでも、私は世の中の虐げられている「しょんべん小僧」達のため、そして「男らしさ」の最後の砦を守るために、男子トイレの「しょんべん小僧」達がどうしたら、放水ミスをしないかを物理的に考えてみることにしたい、と思うのである。
さて、便器まで小便が届かないという「放水ミス」はどのようにすれば防ぐことができるだろうか?小便の飛距離を小さくしないためにはどのようにしたら良いだろうか?そのためには、まず小便の飛距離がどのようにして決まるのかを考えなければならないだろう。
下のちょっとリアルな「しょんべん小僧」の放水作業ではないが、小便の軌跡はきれいな放物線を描く。
 |
すなわち、空気抵抗などは無視した場合のピストルの弾と同じく
- 銃筒の先端を出るときの初速度
- 銃筒の角度
銃筒の先端を出るときの初速度 = V0と表すと、小便の飛距離は
銃筒の角度 =θ
a V0^2 Sin[2θ] (aは定数)と表される。この式を見ればθ = 1/2 rad.の時にSin[2θ]が1になるので一目瞭然であるし、また感覚的にも自然であるが、銃筒の角度の方は上向き45度の角度に向けるときに小便の飛距離は最大になる。一方、初速度V0の方は速ければ速いほど、小便の飛距離は伸びる。
それを示したのが、次の図である。「小便の銃筒の先端を出るときの初速度と銃筒の角度を変えた時の小便の飛距離」を示したものだ。
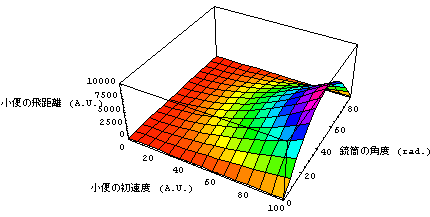 |
すると、便器まで小便が届かないという「放水ミス」すなわち、小便の飛距離を小さくしないためには、銃筒の角度を大きくしすぎたり、小さくしすぎたりしないという知見が得られるわけであるが、そんなことは当たり前だ。誰もトイレで銃筒を真上に向けたり、真下に向けたりはしないのである。先のちょっとリアルな「しょんべん小僧」ではないが、手で放水銃を支持している限り何の問題も無いのである。
つまり、便器まで小便が届かないという「放水ミス」はほとんどの場合「放水銃の角度」のせいではないのである。つまり、「銃筒の先端を出るときの初速度」が問題だったと考えるのが自然である。
それでは、「銃筒の先端を出るときの初速度」はどのようにして決まっているのだろうか?それを大雑把に考えてみたのが次の図である。腹筋で膀胱に圧力Pをかけて、銃筒の先端から小便を初速度V0で放水作業を行うのである。
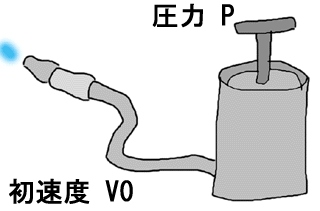 |
ところで、上の絵でポンプとして表した膀胱に圧力Pをかけた場合には、膀胱からb P (bは比例定数)と表せる量の小便が銃筒に送り込まれるものとしよう。その場合、その量の小便が銃筒の先端から単位時間に出るわけであるから、銃筒の先端の口径をAとすれば、
V0 = b P /Aと表すことができる。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのである。
さて、いくら腹筋が強い人であっても腹筋をいきなり締め付けることはできない。つまり、腹筋で膀胱を締め付ける圧力Pというものは徐々に大きくなるのである。
すると一見、「銃筒の先端を出るときの初速度V0」も0から徐々に大きくなる、すなわち、放水作業を開始した最初の瞬間は「銃筒の先端を出るときの初速度V0」= 0であって、小便の飛距離も0である、つまり、便器まで小便が届かないという「放水ミス」が必ず起きるかというと、実はそういうわけではない。
ポンプである膀胱から銃筒の先端までは、ある程度の長さがある。もちろん、その長さは一定ではないのだが、とにかくある程度の長さがある。そのため、小便が銃筒の先端から出る瞬間には、ポンプである膀胱にかかっている圧力Pは0ではないのである。すなわち、膀胱から銃筒の先端まである程度の長さがありさえすれば、「銃筒の先端を出るときの初速度V0」は結構大きくすることができるのだ。もちろん、腹筋を鍛えて、腹筋に急激に力を掛けることができれば、その効果はさらに上がることは言うまでもない。
だとしたら、一般的に便器まで小便が届かないという「放水ミス」は一体何時起きるのであろうか?それは、「銃筒の先端を出るときの初速度V0」を決める膀胱にかかる圧力Pが低下し、なおかつ最初の瞬間と違い「膀胱から銃筒の先端までの長さ」を有効に活用できない、放水作業を終える瞬間である。飛行機でも着陸が一番難しいというが、この放水作業もやはり放水作業を終える瞬間が一番難しいのである。そのため、多くの場合小便達は便器内への着陸に失敗し、便器の下を汚してしまうのである。
しかし、私は「男らしさ」の記念物でもある「立ちしょうべん」を守るために、一つの解決策を考えついたのである。「男らしさ」の最後の砦を守る技術を提唱したいのである。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのであるから、放水作業のラストに膀胱を締め付ける圧力Pが小さくなった、あるいは、膀胱を締め付ける圧力Pを有効に膀胱からの排水に変換できない排水作業のラストにおいて、銃筒の先端の口径Aを小さくしてやればよいのである。そうすれば、「銃筒の先端を出るときの初速度V0」は「銃筒の先端の口径A」に反比例するのであるから、膀胱から出てくる小便の量が低下しても、「銃筒の先端を出るときの初速度V0」を0にならないように維持することができるのである。これにより、放水ミスを防ぐことができるハズなのである。
さて、私は「男らしさ」の最後の砦である「立ちしょうべん」を守るために、このような技術を考えてみたわけであるが、この技術の実証作業は行っていない。果たして、「銃筒の先端の口径A」を自分の意識で小さくすることができるか!?というところに大きな問題点があるような気もするのであるが、それは「男の意地」で克服できると私は信じている。外部から制御するって手もあるのだし。って何の手の話だ、全く。
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2001-01-16[n年前へ]
■バスト曲線その2 今日書いたメール。 
あの方程式は
>液体の圧力は水平方向ではなく表面の法線の方向に働くので
このとおり、表面の法線方向の関係に直されていますし、それが「自由境界におけるLaplace の関係」そのものですよね。
>というのは液体の圧力は水平方向ではなく表面の法線の方向に働くので、
>ヤング率が大きくなる程半球に近付くはずです。
単に液体の自由境界を計算するときと同じように解けば、あの文章の末尾に
>ちなみに「水風船バストモデル」は無重力下ではどのような
>形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。
と書いたように仰るとおり半球に近づくように一見思えます。
ここで無重力下というのは、皮膚の張力が重力に較べて十分大きい、ということなわけで「ヤング率が大きくなる」のと同じなわけです。
ところがところが、です。
「あの方程式を解くときの境界条件は胸板側の長さ・バストの体積を先に決めています。」
また、「あの座標軸の下で方程式を解く」ために、あの方程式はY,B(Y)の一対一の対応を必要としています。それが、「バストが本当に垂れてしまうような状況は考えていなかったりするので」という前提ですね。
この二つの境界条件・前提の下で、「ヤング率が大きくなる程半球に近付くはず」が本当に正しいかどうか、考えてみては如何でしょうか?
この二つの条件を除外しようとすると、方程式を作って解くのがとたんにメンドーになります。
というわけで、一般化されたバスト方程式をぜひ作って解いてみて下さい。
2001-01-27[n年前へ]
■オッパイ星人の力学 仏の手にも煩悩編 
時速60kmの風はおっぱいと同じ感触か?
本サイトhirax.netは「実験サイト」というジャンルに分類されることが多いようである。何が実験で、何が実験でないのかは私にはよくわからないのだが、とにかく「実験サイト」と呼ばれるサイトは数多くある。そして、その数ある実験サイトの中でも、人間そして愛について日夜取り組んでいるサイトの一つが「性と愛研究所」である。その「性と愛研究所」を読んでいると興味深いことが書いてあった。テレビ番組の「めちゃめちゃイケてる!」の中で何でも「時速60キロの風圧はおっぱいの感触である」と言っていたらしい。そしてまた、「性と愛研究所」では「おっぱいの感触と風圧に関する考察」の中で、「時速60kmでは全然おっぱいの感触ではなくて、ちょうど時速100kmを境に急におっぱいの感触を感じます。」というメールを紹介しながら、
「時速100kmの風では、本物は触れないけどお手軽に疑似体験、名付けて『プリンに醤油でウニ』ではなくなってしまう。それでは、まるで『キャビアにフォアグラでトリュフの味』だ。青少年のために疑似おっぱいを探してあげる必要があるな。」と結論づけている。
この「時速60kmの風」現象は「できるかな?」的にとても興味深いと思われるので、今回じっくりと考えてみることにしてみた。そして、この結論に何らかのプラスαをしてみたいと思う。
そう、前回「オッパイ星人の力学 第四回- バスト曲線方程式 編- (2001.01.13)」でオッパイの表面で働いている力について考えてみたのは、実は単に今回・そしてさらに次回の話のための準備だったのである。(さて、ちなみに今回は会話文体をメインに話が進む。「性と愛研究所」ではないが、この手の話は会話文体の方が書きやすいように思うし、私のバイブル「物理の散歩道」でも「困ったときの会話文体」と言われていたので挑戦してみた次第である。言うまでもないが、AもBも私が書いてはいるが、私自身ではない。)
A : 「東名高速で出勤途中に確認してみたんだが、やはり時速100kmあたりが妥当な感じだったな。」
B : 「何を根拠に妥当なのかがよくわからないが、確かに時速60kmでは手に何かが触っているという感触すらないな。それにしても、哀しい出勤の景色だぞ、それ。」A : 「ほっとけ!だけど、少し考えてみると、このおっぱい(ニセモノ)の感触問題は結構面白く、技術的にもなかなかに深い話だと思うんだよ。」
B : 「はぁそうですか…、としか言いようがないな。」A : 「まぁ、聞け。何しろこのおっぱい(ニセモノ)の感触問題には流体力学のエッセンスがぎっしりと詰まっているんだからな。」
B : 「そんな話は聞いたことはないが、とりあえず聞かせてもらおうか。」A : 「このおっぱい(ニセモノ)の感触問題を解くためには、とりあえず車の窓から手を出したときの指の周りの空気流を計算すれば良いわけだ。」
B : 「ちょっと待て。何で指の周りなんだ。手のひらじゃなくて?」A : 「簡単なことさ。試しにおっぱいを揉む仕草をしてみろよ。」
B : 「こ、こうか?あぁっ?手のひらじゃなくて指で揉んでるっ!」A : 「そうだろ。何故かわからないが、おっぱいを揉む仕草=Mr.マリックが超魔術をかける時のような指使いらしいんだよ。」
B : 「うむ、確かにそのようだな。」A : 「だから、時速60kmの風からおっぱいの感触を受けているのは指先だと考えるのが自然だろ。それなら、とりあえず下の図のような「指の間を抜けていく空気の流れ」を計算してみれば、おっぱい(ニセモノ)の感触問題が解けるわけだ。」
B : 「実写の手に二次元の計算結果を三次元的に合成するという凝った処理が、実にクダラナイことに使われている例だな…」
 | 高速で走る車の窓から手を出して、その手の指の間を抜けていく空気の流れを計算しよう。 鉛直方向の指の等方性を考えて、右の図に示すような指を輪切りにするような水平面のみを考える。 こんな写真を撮るときに、自己嫌悪に陥りがちなのは何故だか知りたい今日この頃。 |
A : 「こういう「空気の流れ」ような流体の力学は、ニュートンのプリンキピアに始まり、オイラーとベルヌーイにより非圧縮・非粘性の理想流体の運動方程式とエネルギー保存則が導かれた。それがオイラーの運動方程式とベルヌーイの式だ。オイラーの運動方程式はちなみにこんな感じだ。」
加速度 = 外力 + 圧力勾配力 v : 速度 |
A : 「基本的には「加速度 = 外力 + 圧力勾配力」という形だな。この非圧縮・非粘性の理想流体の場合はラプラシアンがゼロのポテンシャル流れと呼ばれる単純な流れになる。試しに、そんな場合をNast2Dを元にしたプログラムで計算してみた結果はこんな感じになる。ホントはこの計算自体は完全な理想流体ではないのだが、まぁ大体はこんな感じだ。」
B : 「おっ、あっという間に計算したな。」A : 「まぁ、ポテンシャル流れならエクセルでもちょちょいと計算できるくらいだからな。ちなみに、これは窓から手を出してしばらくしてからの空気の流れだ。」
 |
A : 「で、どうだ?」
B : 「いや、どうだ、と言われても困るが、なんかキレイだな。だけどちょっと小さくて見にくいなぁ。」A : 「そう言われれば確かにそうだ。じゃぁ拡大してみるか。」
 |
B : 「で、この結果から何がわかるんだ?」A : 「この図で空気は左から右へ流れているわけだが、左端の空気の速度と右端の空気の速度は、実は同じなんだ。」
B : 「そう言われても、よくわからないが?」A : 「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
B : 「えっ?おかしいじゃないか、それなら逆に言えば指も空気から何の抵抗を受けないってことか?」A : 「そういうことだ。これがダランベールのパラドックスだ。」
B : 「じゃぁ、何か?この指先に感じるまぎれもないおっぱいの感触は幻だとでもいうのか!? そんなのオレは認めないぞ!」A : 「まぎれもない、っていうほどのものでもないし、ニセモノおっぱい自体は何か一種の幻のような気もするが、もちろん感触自体は幻であるハズはない。そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全てはおっぱいの感触を説明するために、だ。」
B : 「それウソだろ。ナヴィエとストークスが聞いたら怒るぞ。」
加速度 = 外力 + 圧力勾配力 + 粘性力 v : 速度 |
A : 「見ればすぐわかるだろうが、この非圧縮流体に対するナヴィエ・ストークスの方程式は、最後に粘性項が入っている以外はオイラーの運動方程式と全く同じだ。」
B : 「なるほど。こうしてみると意外に簡単な式だな。」A : 「あぁ、オイラーの運動方程式に粘性項が入っただけだからな。そのせいで計算はちょっと複雑になるが、最近のパソコンならノープロブレムだ。というわけで、粘性を考慮して計算してみた結果が次の図だ。」
 |
B : 「おっ、ちょっと様子が違うな。何か、ジェットエンジンみたいに尾を引いてるぞ。」A : 「そうだろ。指の後ろのl様子がずいぶんと違うだろう。で、これを拡大してみたのが次の図だ。」
 |
B : 「左端の空気の速度はもちろんさっきと同じだが、指の後ろでは空気が渦巻いているし、右端の空気の速度は全然違うな。」A : 「もっとリアルに、窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみた計算結果のアニメーションが次の図だ。指の周りに空気が渦巻いていく様子がよくわかるハズだ。」
 | 窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみたもの。指の周りに空気が渦巻いていく様子がよくわかる。 メッシュを細かく切ったおかげで、計算結果は1GB弱。なんてこったい。 |
B : 「指が空気の中を走り抜いていく様子がよくわかるな。確かにこれなら、空気の抵抗を受けまくりだな。」A : 「そうだ。空気は指から力を受けるし、逆に、指は空気からしっかりと力を受けるわけだ。」
B : 「なるほど、この計算結果は指先に感じるまぎれもないおっぱいの感触を説明しているわけだな。いい感じじゃないか。流体力学そして粘性項さまさまじゃないか!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「おやっ?ちょっと待てよ!これでは、ただ現実を説明してみただけで、何の解決にもなってないぞ!時速60kmと時速100kmの風の感触の差を説明しているわけでもないし、青少年のためのもっと安全な擬似おっぱいを提供しているわけでもない!」A : 「いや、それがそういうわけでもない。実はこの先があるんだ。このナヴィエ・ストークスの方程式の解はレイノルズ数という無次元数によって決定されるんだ。今回の場合で言うと、レイノルズ数は「指の直径x 車の速度 / 流体の運動粘性率」という形になる。そして、このレイノルズ数が大きくなるほど渦が延びていくんだ。」
B : 「なるほど、わかってきたぞ。つまりあれだな。時速60kmから時速100kmに速度を上げれば、それに応じてレイノルズ数が大きくなって、空気の渦もおおきくなるし、おっぱいの感触も確実なものになるわけだな。勉強になるな。」A : 「う〜ん、実際には密度の違いの方が大きいんだが、ナヴィエ・ストークスの方程式の理解としてはそれでいいかもな。あと、単にレイノルズ数を大きくしたかったら指を太くする、っていうのでもいいわけだ。」
B : 「そう言われても指の太さはなかなか変えられないしなぁ。」A : 「指サックとか色々手はあると思うが、もっといい方法がある。さっきの式を眺めてみれば流体の運動粘性率が小さくなれば、レイノルズ数は大きくなる。例えば、水の運動粘性率は空気のそれの十五分の一だ。」
B : 「ってことは、水の中だったら、レイノルズ数も大きいし、密度も大きいし、指先に抵抗を受けまくりってことだな。すると、水中で手を動かしてみれば、それは空気中の高速クルージングと同じってことになるな!」A : 「そうさ、風呂の中で手をひとかきすれば良いだけの話さ。何もわざわざ時速100kmの車の窓から手を出す必要はないんだ。実際、風呂の中で確かめてみたけど、なかなかイイ感じだ!」
B : 「時速100kmで走る車の窓から手を出すのに較べれば、風呂の中で手をひとかきすれば良いだけなんて、まさに青少年のためのもっと安全な擬似おっぱいだな!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「それはもういいっ言ってるだろ。」A : 「ところで、ふと考えてみたことがあるんだ。さっき、指を太くすれば遅い速度でもレイノルズ数が大きくなるって言っただろ。東大寺の大仏なんかかなり指が太いじゃないか。」
B : 「確かに、そうだな。」
A : 「今調べてみると、大仏の掌の長さは256cmだ。つまり普通の人間の10倍くらいある。だったら、指の太さも10倍はあるだろう。ってことは、ほんのそよ風が吹いただけでも、大仏の手にはしっかりとしたおっぱいの感触が感じられているんじゃないのかな?」
B : 「単に手が大きいから空気の抵抗も大きいだけどいう気がしないでもないが、指の長さもでかいしさぞかし超巨乳の感触かもしれんな!そう考えると、あの大仏の手も何か実にイヤラシイ手つきに見えてくるから不思議だな!」A : 「う〜ん、悟りを開いているから、指先のヘンな感触なんかには惑わされないんだとは思うけどな。しかし、案外と仏もそんな煩悩と日夜闘っていたりするのかもしれないなぁ。しかも、その煩悩がホントーにあるのかもよくわからない幻のような擬似おっぱいってところが面白くないか?大仏の指先は二十一世紀の煩悩そのものを暗示しているのかもしれん。仏の手にも煩悩ってところだな!」
B : 「言いたい放題だな、全く。」
さて、今回は「オッパイ星人の力学第四回 - バスト曲線方程式 編- (2001.01.13)」と繋がるところまで話が辿り着かなかった。おっぱいの表面張力、マボロシのような指先の流体力学、そして大仏の煩悩をめぐる大河ドラマは人生そのもののようにまだまだ続くのである。
2001-09-25[n年前へ]
■純愛で世界を描ききれ 
Study of the Regular Division of the Plane with Innocent Love
先日、出張先で話をしようとした途端、いきなりこんなコトを言われた。
「最近、更新頻度が下がってますねぇ、あとアッチ系のネタが多いですねぇ。」また別の人には、
「たかが風圧がオッパイに思えるものでしょうか?自分には、そこがなんとも不思議で納得できないのであります。」などと言われた。本来、私は真面目な話をしに行ったハズなのであるが、思わず弁解したくなって、
「一体、指の何処でその感触を感じると思われますか?」
「それに、モンローウォークの動画はまるで全裸みたいに見えて、思わず自分はウィンドーを閉じてしまったのであります。」
「いや、掌の広げ方次第で、空気が指に与える圧力が動的に変化するのだが、その指の動きに応じて動的に弾力が変化するさまがアノ感触に近いという想像は如何なものだろうか?たかが風圧、されど風圧、と謙虚に考えるべきではないだろうか?」とか
「空気流が指の側面を押す力が主たる個所だろう、それすなわち、指の周りからこぼれるおちるアレが指に与える感覚なのである。」とか、
「実はOLスーツ編の動画も作成したのだが、そっちの方が私的にはイヤラシク倫理的にNGだったのだ。」とか色々言ってしまったのである。しかし、実はその話をしている仕事場には他にも人が何人もいて、しかもその人達には私は面識は無い。ということは、私は他人の仕事場にイキナリ来たと思ったら、「アノ感触」とか「OLスーツ」とかそんなことを話し出すトンデモない奴にしか見えないのである。これはちょっといけない。いや、かなりマズイ。
そこで、そんなことを言われないために、今回は「できるかな?」のスタート地点である「画像」の話題を考えてみたい。しかも、ただ考えるだけではつまらないので、「できるかな?」風に「愛」を込めて「画像」について考えてみたい、と思う。というわけで、今回は題して「純愛で世界を描ききれ」である。
八月に台風が関東地方を直撃した日、私は東京タワーのすぐ横で「高画質化のための画像処理技術」という研究会を聴講していた。会場に辿り付くまでの間ひどい雨と風に襲われて、最初のうちは「こ・これは、風速25m/s位はあるな。ってことは25mx 3600 s /1000mで時速90kmか…ってことは、計算によればE〜Fカップが今まさに体中にぶつかってきているのかぁ!」なんて(自分を元気づけるために)考えていたのだけれど、風だけでなくて雨もひどかったので、ついには濡れねずみになってしまい、ただ「………」と何も考えずとぼとぼ歩くだけのゾンビ状態になってしまった。
何はともあれ、そんな感じでやっとのこと会場に辿り付いて、いくつかの話を聞いていたのだけれど、その中でもとても面白かったのが、大日本印刷の阿部淑人氏の「シミュレーテッド・アニーリングによるディザマトリックスの最適化」という話だった。色々な項目を適当に重み付けしながら、ハーフトーンパターンを自動で生成して、理想のハーフトーンパターンを作成しよう、というものである。その話の後半では、工芸的なスクリーンの話も俎上に上がり、M.C.Escherの"Sky& Water I"をグラデーションの例に挙げてみたり(残念ながら実際にそんなハーフトーニングをしたわけではないが)、菩薩像を般若心経でハーフトン処理してみせたり、となかなか「できるかな?」心をくすぐるものだった。そこで、私も似たようなことにチャレンジしてみて、さらにはM.C.Escherの版画を使ったハーフトーニングを行ってみたいと思うのである。
 |
そもそも、ハーフトーニングとは多値階調を持つ画像などをニ値出力の(もしくは少ない階調しか持たない)機器で出力するために、多値の階調をニ値(もしくは少ない階調)の面積比率で置き換えることにより出力する方法のことである。例えば、下の例はグレイスケールのグラデーションパターンを円スクリーンによりハーフトーニングしたものである。
 上を円スクリーンによりハーフトーニングしたもの  |
Photoshopを使っている場合には、簡単に任意形状のハーフトーニングを行うことができる。例えば、こんなパターン![]() をカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
をカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
という風にニ値化ハーフトーニングを行うことができる。ところが、じゃぁこれと同じようにEscherの版画を使ってハーフトーニングしようと思っても、そう簡単にできるわけではない。なぜなら、このハーフトーニングが明暗比較によって行う以上、ハーフトーニングに使うパターンは多値の画像でなければならないのである。
Escherの版画も版画という(例えば白か黒かといった)ニ値の出力機器を用いているため、やはりニ値の画像に過ぎない。例えば、下の版画はEscherの”Studyof the Regular Division of the Plane with Horsemen”である。
 |
上の版画の一部を(ちょっとだけ細工をしつつ)抜き出してみたのが下の画像だが、白黒半分づつのニ値画像であることがわかるだろう。また、きれいな繰り返しパターンになっていて、平面にこのパターンできれいに埋め尽くすことができるのがわかるだろう。
 |
この画像をPhotoshopのカスタムパターンを用いて、グレイスケールをニ値化ハーフトーニングすると、この画像がニ値画像であるため、下のように階調をきれいに出力することができず、結局のところ「黒か白か」といった階調飛びの画像になってしまうのである。
 |  |
そこで、まずはニ値の画像を元に多値のハーフトーン用パターンを作成するプログラムを作成してみた。作成するやり方としては、初期値を元にして暗い方。明るい方それぞれの方向にローパスフィルターで演算をしつつ、256階調分のハーフトーンを作成し、さらにそれをPhotoshopで処理できるように多値画像として出力することができるようにしてみた。先の発表のやり方で言えば、「高周波を減らす」という項目に重みをおいて、ハーフトーンパターンを自動生成するアプリケーションを作成してみたわけだ(バグ満載状態で)。説明は一切無し、しかもボタンを押す順番を間違えると上手く動かないという状態ではあるが、一応ここにおいておく。名前はhiraxtone.exeでバージョンは0.0…01という感じである。(白黒ニ値だけど24bitモードの)Bitmapファイルを読み込んで、多値のスクリーンを生成するようにしてある。
それでは、このhiraxtoneを用いて、ニ値画像を元に作成した多値階調ハーフトーンパターンの一例を次に示してみる。これは、先の"Studyof the Regular Division of the Plane with Horsemen"の一部分を縮小したニ値画像をもとにして処理してみたものである。 |  |
でもって、上で作成した多値階調ハーフトーンパターンを用いて、グラデーションパターンをハーフトーニングしてみた例が下の画像である。「単純にパターンニ値化した場合」と違って、「hiraxtone1で作成したパターンを使用した場合」はグラデーションが保持されているのがわかると思う。また、階調が保持されているというだけではなくて、まるでEscherのオリジナルの"Studyof the Regular Division of the Plane with Horsemen"のようなパターンにできあがっていることも判ると思う。
 |  |  |
さて、ニ値画像パターンを利用してハーフトーニングすることができる、となると他にも色々と遊ぶことができる。例えば、自分だけのハーフトーンパターンを作ってみたくなることだろう。そして、さらにはその素晴らしいスクリーンに自分の名前を付けて広めてやりたい、と思うのは至極当然の話である。古くはBayerなどがそうしたように、自分が作ったスクリーンに自分の名前をつけてみるわけだ。
とはいえ、私が仮にスクリーンを作成してみたところで、そのスクリーンを私の名前で呼んでくれる保証はどこにもないのである。そこで、卑怯な手ではあるが、自分の名前を元画像にしてスクリーンを作成してみることにした。こうすれば、否でも応でもこのスクリーン形状を呼ぶために人は私の名前を使うことになるわけだ。
というわけで、私の名前「純」という漢字を元データにして、ハーフトーンスクリーン「純」を作成してみた。また、「純」とくれば当然もうひとつ「愛スクリーン」もさらに作ってみた。いや、別に「純愛」を目指そう、と気負っているわけではなくて、単にうちの兄弟は長男が「純」で長女が「愛」なのである。いや、少し気恥ずかしいけど、ホントの話そうなのだからしょうがない。
さて、作成した「純・愛スクリーン」さえあれば、「純愛」で世界を描ききることができるわけで、早速描いてみたのが、下の仲間由紀恵である。オマエの世界イコール仲間由紀恵か?とか、ソレってホントに「純愛」か?とか、つまらないツッコミを入れられそうな気もするが、そんなことはどうでも良いのだ。私はTRICK以来仲間由紀恵のファンになってしまったのだから、しょうがないのである。そしてまた、「純愛」を馬鹿にしてはイケナイ、と私は少しばかり思うわけなのである。(私の名前だから)
 |  |
上の二枚をじっくり眺めてみると、結構キレイに仲間由紀恵が描かれていることが判ると思う。しかも、他でもないこの二枚の画像において、私は「純愛」で仲間由紀恵を描ききっているのである。これより、「純」で「愛」な仲間由紀恵はそうそういないハズなのだ。きっと、本物の仲間由紀恵が見たら「何てピュア〜でラブリーな私かしら。きっと、これを描いた人は心のキレイな人なのね!」と感激すること間違いなし、なのだ。
ちなみに、「純愛スクリーン」でハーフトーニングした仲間由紀恵の左眼の部分を拡大してみたのが下の二枚の画像である。瞳の奥にも、「純」と「愛」が溢れていることが判るハズである。それは言い換えれば、この仲間由紀恵の瞳は「純」イコール「私」で満ち溢れ、さらにはその瞳は「愛」で満ち溢れているのである。
(目の部分の拡大図) 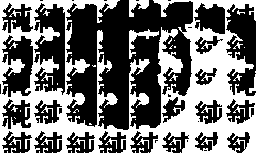 | (目の部分の拡大図)  |
う〜ん、正直ちょっとムナシイけれど、だけどちょっと気持ちが良いのもまた事実なのである。やはり、「純・愛スクリーン」で描かれる世界はとても素晴らしい世界なのである。そうなのである。
さて、今回作成したhiraxtoneは、実際のところ自分でも言うのもなんだが、本当のところ今ひとつキレイな出力ができないし、大体思ったように動いてくれないのである。低周波優先として重み付けをしたハズなのに、どうもそんな風に動いていないし、計算にも時間がかかりすぎる。全てはビールを飲みながら行き当たりばったりにプログラミングするところがいけないのかもしれないが、どうも今ひとつなのである。また、本来であればもう少し元データの形状を残すことを優先(それは高周波優先にならざるをえないだろう)にするようなオプションもつけてみたいのである。
が、とはいえ今回はいい加減思いページになってきたこともあるし、ちょっと疲れてきたこともあるし、とりあえず「純愛」で世界を描ききったところまでで今回は終りにして、続きは次回以降に遊んでみたいのである。