hirax.net::Keywords::「学校」のブログ

■世間は上等な学校じゃねえんだよ。　

上等な私立卒業したって、世間は上等な私立じゃねえんだよ。
　　　西原理恵子

■（日本の）学校で正解が一つの問題ばかり解き続けること　

　週刊SPA! 鴻上尚二　ドン・キホーテのピアス 707 「騒動になった熊本県の社会科」テストを考える　の一部を要約するとこうなる。

　人生の正解は一つに決まらないにも関わらず、（日本の）学校では（用意された）正解が一つの問題ばかり解き続ける。そして、実社会に出たら、正解は一つじゃないという当たり前のことに気づき、愕然とする。

■教育費と茄子の花は千に一つも徒はない　

　スラッシュドットでのコメントから知った、西原理恵子の言葉（毎日新聞の元記事）。
　西原理恵子の言葉だけをひきたいところだけれども、文脈背景の紹介上、林真理子の言葉も引用する。

林真理子＞　独身のお金持ちの友人が電話してきて「私たちが払った税金をヤンキー（不良）の子に使われるのは嫌だ。民主党は何を考えているのか」と言っていた。

西原理恵子＞　子どもが大きくなって年金を払い、高齢者を養うんですよ。ヤンキーが将来刑務所に行けば、もっとお金がかかる。人を人とするためには教育と職業が必要。それは国家が何よりも先にやらなければならないこと。議員の給料払うなら、ヤンキーの教育費に使え。

　教育・職業といったことは、西原理恵子のマンガ中で語られるリフレインのひとつだ。たとえば、「営業ものがたり 」なら「うつくしい　のはら」あるいは、「朝日のあたる家」といったマンガ中に、繰り返し登場する。あるいは、対談でも時折口にする。

私はまいにち字をならいに行く。
字をおぼえましょう。
字がよめたら　世の中がわかる。
商売ができる。ごはんが買える。

「うつくしい　のはら」冒頭

　「親の意見と茄子の花は千に一つも徒はない」ということわざがあるが、教育費もそういうものかもしれない。…うーん、そんなこともないか。

　教育とは、学校で習ったことをすべて忘れた後に残っているものである。

アルベルト・アインシュタイン

■初恋相手までの距離は30cm　

　あなたの初恋の相手はどんな人でしょうか。…たとえば、初恋相手の名字はどんな名前でしょうか？

　私の初恋相手は名字が「は行」で始まる人でした。それが一体どういうことかというと、学校の教室には五十音順で男女の机が並べられ・２つの机ごとにくっつけられていて、名字が「は」行で始まる「”ひ”らばやし」くんは、隣の人（机を並べている人）を好きになったのでした。実に単純です。

　世界は広く、数十億人の人たちが地球の上で暮らしています。世界も・地球も広大です。しかし、こと「初恋相手までの距離」となると、実は意外に狭いのではないでしょうか？たとえば、私のような「机を隣り合わせた相手に生まれて初めての恋をする」といった単純明快近視眼的な人だって多いのではないかと思います。

　なにしろ、人気マンガ「タッチ」の主人公兄弟たちだって、幼なじみのお隣さん（浅倉南ちゃん）が初恋の相手でした。…そんなマンガの主人公たちそと同じように、向こう三軒両隣な「ご近所さんのお隣さん」が初恋相手だという人も、無視できない数いるのではないか、と想像します。

　初恋相手の名前を思い浮かべてみれば、「五十音で同じ行（列？）だったりする人の比率が有意に高い」のではないでしょうか？たとえば、あなたとあなたの初恋相手を思い浮かべると、実は五十音が近かったり＝出席番号順が近かったり、あるいは、身長順が近かったりするということもあるかもしれません。 五十音順とか、身長順とか、（平安時代なら）いろは順とか…そんな「ルール」に従った距離が近い辺りで初恋が生まれていたりすることもあるのではないでしょうか。

　今日立てた仮説は、「日本では、自分の名字と初恋相手の名字の五十音には（田舎の名字比率を考慮しても）相関がある」というものです。それは、初恋相手までの距離は意外なほどに手近かであるという「初恋相手までの距離は30cmの法則」です。（…その30ｃｍが無限に遠かったりするんですけど、ね）

■「トラック曲線＝（半円＋直線）×２」という運動会シーズンのナゾ!?　

　秋といえば運動会の季節です。この季節になると、いつも頭に浮かぶ「謎」があります。…それは「徒競走」をする校庭にある「トラック」の形に関する疑問です。

　校庭のトラックは「両端の半円を直線で結んだ形」です。…はい、勘が鋭い人であれば、もう気づいただろうと思います。運動会シーズンにいつも考え込んでしまう謎というのは、なぜ

トラック曲線＝（クロソイド曲線＋円弧＋直線）×２

トラック曲線＝（半円＋直線）×２

　「トラック」の形状が「直線と半円」で形作られているとすると、直線コースから半円部分に突入した途端、急に、曲率がゼロからある程度大きな値に変わってしまいます。言うまでもなく、直線とは「曲率がゼロである」真っ直ぐな線であり、円とは曲率が一定の曲線であるからです。ということは、トラックを走るランナーたちは、体が進む方向を決める”ハンドル”をいきなり切らなければなりません（下図の黒線トラック）。

　しかし、高速道路のカーブと同じように、トラックのカーブにおいて直線と円弧部分をクロソイド曲線で繋いでおいたならば、最初から最後まで曲率が滑らかに変化していきます。クロソイド曲線というものが、曲率を連続的に変化させていく曲線なので、曲率ゼロの直線と任意の有限曲率を持つ円弧の間を、クロソイド曲線は滑らかに繋ぐことができるわけです。 　ということは、トラックを「（クロソイド曲線＋円弧＋直線）×２」という数式で記述したならば、ランナーは限りなく滑らかに・自然にトラックのカーブを走り抜けていくことができるはずなのです（下図の青線トラック）。

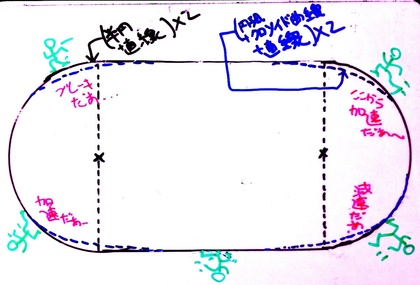
　それにも関わらず、学校の校庭にあるトラックが、すべて（半円＋直線）×２という数式でトラックが形作られているからには、きっとそれなりの理由があるのだろう、と思います。その理由を知りたい…というのが「この季節になると、いつも頭に浮かぶ疑問」なのです。