2008-07-18[n年前へ]
■エクセルでシミュレーション Vol.1 [静電界準備 編] 
 「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは(私たちのような勉強世界からの REST OF US にとっては)とても素晴らしいと思います。
「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは(私たちのような勉強世界からの REST OF US にとっては)とても素晴らしいと思います。
ところで、現在では”表計算プログラム=マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。
 自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」をしてみました。
自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」をしてみました。
まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。2次元世界を離散化するということは、エクセルの表がそうであるように「世界(画面)をセルで分割する」ということです。

上で(x,y座標空間での)差分方程式にしたものを、さらにエクセル(表計算ソフトウェア)で解くときのやり方を図解したものが下の図です。「ある点の電位(φ)は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。
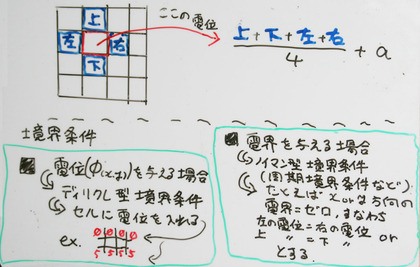
また、2種類の境界条件(電位を指定するディリクレ条件/電界を指定するノイマン条件)をどのようにエクセル上で処理するか、というのが下の部分になります。
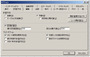
こういったセルの値が「(そのセル自身を含む)セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。

以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。
2010-08-23[n年前へ]
■離散化した「微分方程式」を描いて遊ぶのにお勧めなプログラミング言語は何でしょうか? 
 ふと思い立ち、とある技術雑文を書き始めました。内容は、適当な物理現象のふるまいを数式で記述して、その動きを把握すると同時に・その物理現象をどのように制御したら良いのかを考えてみよう、というものです。
ふと思い立ち、とある技術雑文を書き始めました。内容は、適当な物理現象のふるまいを数式で記述して、その動きを把握すると同時に・その物理現象をどのように制御したら良いのかを考えてみよう、というものです。
物理現象のふるまいを記述し・解析してみようとする時、とりあえず簡単な方法として「微分方程式モドキを書き、その動きを眺めてみる」というものがあります。「一瞬のふるまいを記述する」ような微分方程式や、差分方程式や、あるいは、漸化式のようなものをまずはラフスケッチのように描いてみて、あとは、初期条件を決めることで「すべての瞬間のふるまい」を追いかける、というようなやり方です。そして、その動きを眺めてみるわけです。
 …すると、そんな作業は、数列(というかベクトル列)を再帰的に解かせる記述をする作業になることも多いように思います。そんなとき、実際に計算もさせつつ、そんな記述を行うときには、一体どんなプログラミング言語が良いのだろう?とふと考えました。…なぜかというと、再帰的な定義式を書いたあとに、計算速度向上やオーバーフローを防ぐために、いつもそのコードをループ文で書き直す作業をしていることにようやく気付いたからです。…こんな作業は(自分でやらずとも)自動的に行ってくれる処理系は絶対あるはずだ、ということにようやく今更ながらに気付いたのです。
…すると、そんな作業は、数列(というかベクトル列)を再帰的に解かせる記述をする作業になることも多いように思います。そんなとき、実際に計算もさせつつ、そんな記述を行うときには、一体どんなプログラミング言語が良いのだろう?とふと考えました。…なぜかというと、再帰的な定義式を書いたあとに、計算速度向上やオーバーフローを防ぐために、いつもそのコードをループ文で書き直す作業をしていることにようやく気付いたからです。…こんな作業は(自分でやらずとも)自動的に行ってくれる処理系は絶対あるはずだ、ということにようやく今更ながらに気付いたのです。
 再帰的なコードを書いたら、あとはそれをループ処理に変え最適化を行ってくれる「いわゆる末尾最適化」をしてくれるプログラミング言語にはどんなものがあるのでしょう?Scheme、Haskell…それともそれ以外の何かでしょうか。離散化した「微分方程式」で遊ぶのにお勧めのプログラミング言語は何でしょうか?
再帰的なコードを書いたら、あとはそれをループ処理に変え最適化を行ってくれる「いわゆる末尾最適化」をしてくれるプログラミング言語にはどんなものがあるのでしょう?Scheme、Haskell…それともそれ以外の何かでしょうか。離散化した「微分方程式」で遊ぶのにお勧めのプログラミング言語は何でしょうか?
2014-05-27[n年前へ]
■エクセルでラプラス方程式を解いて「血管がある皮膚周りの光強度分布」を計算してみよう!? 
 赤い血が流れているはずの血管が青く見える理由で行った計算を大雑把に解けば、たとえば完全拡散体として扱うことができます。それはすなわち、任意の微小領域が周囲に発する光強度は周囲(の微小部分が発する光強度)の平均値になるということで、つまりはラプラス方程式で表される解になります。
赤い血が流れているはずの血管が青く見える理由で行った計算を大雑把に解けば、たとえば完全拡散体として扱うことができます。それはすなわち、任意の微小領域が周囲に発する光強度は周囲(の微小部分が発する光強度)の平均値になるということで、つまりはラプラス方程式で表される解になります。
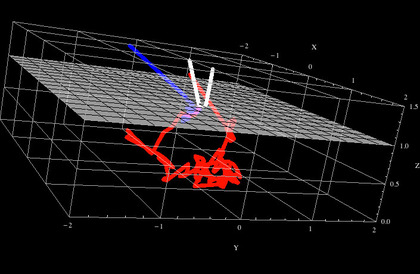
…というわけで、ラプラス方程式を離散化して、お手軽なエクセルで「皮膚内部に血管がある時の、その周辺の皮膚内部・表面での光強度分布を(たとえば青色波長で)可視化してみたのが下図になります。エクセルの各セルは離散化された空間上の各領域を示していて、そこに示されている色と値が光強度を示しています。
画面真ん中辺りに(画面=シート鉛直方向に)血管が流れていて、画面=シート上側にあたるのが皮膚表面です(画面下側が皮膚最奥部です)。

さらに青色・赤色波長の「(光が散乱して方向を変えるまでの)平均自由行程」を踏まえて、表面での光強度分布の違いを描いてみると、限りなく大雑把な近似に基づいた計算をすると、下図のような感じです(縦軸はその波長における周辺近傍の平均強度を基準にした相対値です) 。
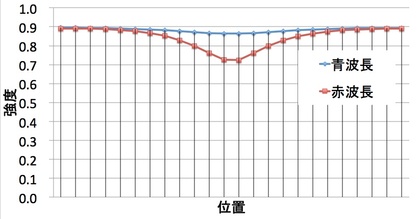
血管が下部にある部分を眺めると、青色波長では、その周囲の部分とさほど変わらない光を発しています。けれど、そこを赤色波長で眺めれば(表皮近くの毛細血管ではなく)皮膚下部に流れる血液に光が吸収されて、光強度が(近傍周囲より)減少していることがわかるかと思います。…だから、赤い血が流れているはずの血管が(周囲に対して相対的に)青く見える、というわけです。