hirax.net::Keywords::「数値計算」のブログ

■風呂場の水滴を考える。　

オールヌードの研究員

　風呂場の天井から浴槽めがけて、水滴がしたたって音がしているのはよくある風景である。ピーンという(もちろん人によっても印象は違うのだろうが)気持ちのいい音がしている。似たようなものとしては、水琴窟などもある。この音がなぜ鳴るかは、ロゲルギストの「物理の散歩道」に詳しい考察がある。それによれば、水滴が一粒落ちたように見えても、実は何粒かに別れており、ちょうどカルガモの親子のようになっているという。つまり、大きな親の水滴の一粒の後を、何粒かの小さな子どもの水滴が追いかけているという具合である。まず、水滴の親が水面に空洞をつくり、その中に子どもの水滴が飛び込むことにより音が出るという。結局、水滴の音を作っているのは、その子どもの水滴の方だという。「物理の散歩道」の中では、針をつたって水滴を落とせば、子どもの水滴ができないという。

　風呂に入って、濡らした手から水滴を落としてみる。指の爪の先から水滴を落とすと音はほとんどしないが、指の「はら」から落とすと派手に音がする。ぜひ、自分でも確かめていただきたい。
　爪先は比較的尖っているので、落ちる水滴は一粒だが、比較的平らな指の「はら」からの場合には、カルガモ親子のような水滴が落ちているせいだろう。

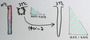
　なぜ、このような違いが生じるかを推測してみたい。まずは、下の絵を見て欲しい。

左は指の「はら」から落ちる水滴、右は爪の先から落ちる水滴、いずれも想像図

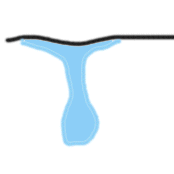　上の上手な絵が言いたいのは、次のような推測である。

• 平らな表面から水滴が落ちる際には、長く伸びた水のブリッジが出来ていて、1つぶ目の水滴が落ちた後も、このブリッジ部分が「カルガモの子ども」のように小さな水滴となって後を追いかけていくのではないか。
• それに対して、尖った表面から水滴が落ちる際には、先のブリッジ部分のほとんどは水でないため、後続の水滴は発生しない。

　計算モデルとしてどのようなものを使うかであるが、私の知っている範囲では大きく分けて2種類のやり方がある。

• 流体をモデル計算する。すなわち、Navier-Stokesの方程式を解く。
• 流体を粒子のようなものの連続体として解く(ex.格子ボルツマン法)

電気通信大学情報工学科情報数理工学講座渡辺研究室( http://assam.im.uec.ac.jp/fluid.html )

水滴が分離する直前 ( http://assam.im.uec.ac.jp/fluid.html)

　また、水滴が水面に衝突する状態の計算は、電気通信大学情報工学科情報数理工学講座渡辺研究室にもあるし、他にもNaSt2DというFreeの2次元Navier-Stokes方程式のソルバーを用いて行われた計算結果が
http://www5.informatik.tu-muenchen.de/forschung/visualisierung/praktikum.html
にある。

水滴の水面に衝突する瞬間 (http://www5.informatik.tu-muenchen.de/forschung/)

　Michael Griebel氏らによるNast2Dのコードは公開されているので、その中身をいじりながら、計算を行う予定である。

　とりあえず、今回はバックグラウンドを紹介する所までで、次回(といってもすぐではないだろう)に計算の本番に入りたい。

　手のひらの実験から考えると、風呂場で水滴の音が聞こえるのは天井が平らなせいだということになる。ならば、鍾乳石のようなつらら形状の天井の風呂場では音がしないのだろうか？しかし、水滴は空気中で落下していく最中には空気の抵抗をうける。そのため、大きな水滴は落ちる最中に分裂し、複数の水滴になってしまう。
となると、

• 落ちる水滴の最初の大きさは、どう決まっているのか。
• 水滴は落下するスピード、水滴の大きさがどの程度になると分裂するのか？

　ところで、インクジェット方式のカラープリンターも液滴で画像を描くのだから、液滴の様子は重要な筈である。液滴が飛び散ってしまっては困るし、位置がずれても困る。各社ともカルガモの子ども水滴をなくすために色々工夫をこらしている筈だ。
　実は風呂場の水滴問題は重要で、奥が深いのだ。オールヌードで私は考えるのであった。

■ATOK用perl機能追加プラグイン　

　ATOKの変換機能を使ってperlのコマンドを使うことができる「ATOK用perl機能追加プラグイン」を作ってみました。これは、以前作ったATOK用コマンドライン機能追加プラグインを機能縮小・変更したものです。動作するためには、ATOKとperlがWindowsにインストールされている必要があります。

　このソフトウェアを使うと、ATOK上で半角英数で入力中に、例えば

print sin(3)/5

0.0282240016119734

system(calc)

while(<>){print $_;}

print sin(3)/5=

print sin(3)/5 = 0.0282240016119734

■計算ソフトsf　

　行列ベクトル演算も含む数値計算に特化した計算ソフト「sf」　久しぶりに、AmetMultiを引っ張り出して、組み込んでみようか…。

■ゴールデンボールズの放熱問題を解いてみる!?　

　中国語の金玉と日本語の金玉と全然意味が違うという話をしていると（「金玉満堂」と「福来る」）、「日本語の方の語源は何に遡るのか？」「日本語の方が指し示すものの”しわ”は放熱のためか？」という全く別の２つの話題となった。「”しわ”は放熱のためにある」ということの真偽はわからないけれど、もしもその放熱効果を考えてみるならば、”しわ”があることによって、一体どのように効率的な冷却が行われるものだろう？

　放熱・冷却の効果は、皮膚の表面における"各領域での(皮膚と空気層の)温度差"を表面積にわたって積分したものに比例しそうに思える。また、皮膚内部における伝熱も重要であるに違いない。大雑把にラクガキしてみれば、それは下の図の「緑色の面積が大きいほど放熱・冷却効果が大きい」というイメージになる。

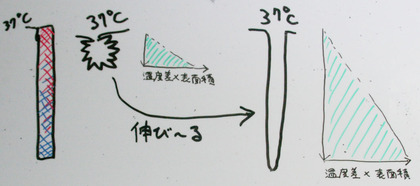
　皮膚の”しわ”の効果、表面積の増加、”しわ”が伸びることによる”皮膚と空気層の温度差"の増加、あるいは、（体の）本体と離れることによる伝熱の違い……などを考えていくと、答えを解析的に解くのは困難であるように思える。

　暑い夏になった頃、夏休みの宿題がわりに"エクセルで金玉の放熱問題を数値的に解いてみる"ことにしよう。暑さを吹き飛ばす放熱問題を解いてみることにしよう。

■光スペクトル操作用のMathematicaライブラリ　

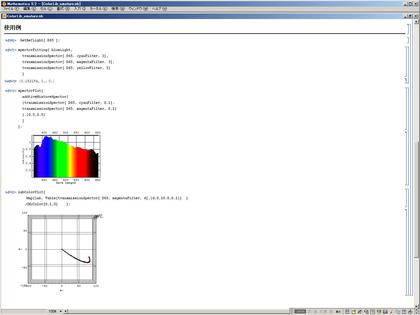以前、Mathematicaの演習用に作った「スペクトル操作用Mathematicaライブラリ」を少し直したので、ここ（”ColorLib_amature.nb”に置いておきます。以前作ったものと同じく、スペクトル・データをリストのような離散データではなくて、関数として（純関数＝無名関数として、あるいは、明示的な関数として）取り扱うという点が特徴だと思います。「（せっかくMathematicaで解くのですから）解析的に解く」「使用者には離散化・数値計算など、面倒くさい汚い部分は見せない・見たくない」という方針で作ったものです。

以前のものからの変更点としては、"spectorPlot"や"labPlot""labColorPlot"など、関数名のMathematicaの命名規則に合わせた変更、加法混色・減法混色用関数の追加・グラフ表示関数の追加・バグ修正といったところです。

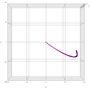
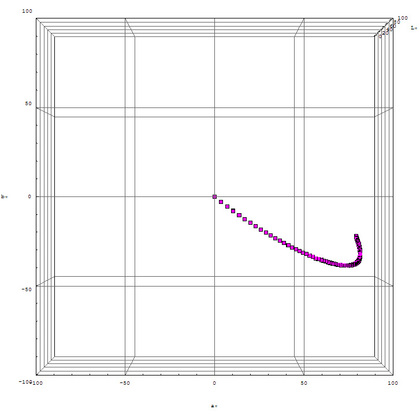　最初のラフスケッチが、絵画の原理を自分なりにおさらいするためのものだったので、濃度変調・面積変調などを扱おうとする場合には、比較的簡単に・気持ち良く作業ができると思います。たとえば、下記のようなコードを書けば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の具合を CIE Lab 空間で眺めたりすることができます。

labPlot[
　Map[lab,
　　Table[transmissionSpector[D65,
magentaFilter, d],{d,0,10.0,0.1}]
]
];

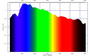
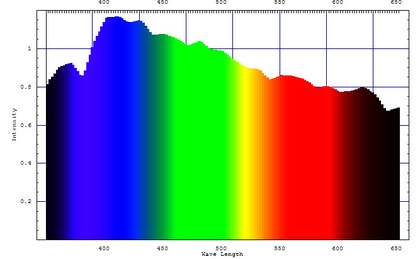　また、白色光照射時に黄色い絵具を塗り拡げる面積を増やしていった場合の反射光スペクトル変化をアニメーションとして作成・グラフ表示するコードはこんな感じです。"addtiveMixtureSpector"は加法混色用の関数で、"transmissionSpector"は減法混色用の関数です。お遊びソフトですが、色々遊ぶこともできるかもしれません。

Map[spectorPlot,
Table[
addtiveMixtureSpector[
{whiteLight,
transmissionSpector[whiteLight, yellowFilter, 1]},
{1-r, r} ],{r,0,1,0.1}]];