hirax.net::Keywords::「表計算」のブログ

■あみだくじシミュレーションをエクセルでプロトタイピングしてみよう　

　「電子ペーパー」でもあるエクセルは、プロトタイピングに向いている。と書いたので、今日は「あみだくじシミュレーション」をExcelで適当に書いて（描いて）みました。そうでした、私は自分自身で作ることが好きなのでした。

作成したエクセルのファイルは、ここに置いておきます。ワークシートの説明（あるいは修正）や、ワークシートを使って色々なことを考えてみよう、ということは明日以降にしてみようと思います。とりあえず、このエクセルのワークシートを実行しているところを動画キャプチャしたものが、下の動画です。

　このエクセル・ワークシートは、循環参照を使い、また計算順序を考慮したバッファリングを使うことで計算が成り立っています。ただし、エクセルの実装の仕組みのために、手動計算を行うためにF9を押しっぱなしにしても、反復計算が全セルに渡って行われるわけではないように思えます(これは検証していない未確認情報です）。そのため、計算を確実に行わせようと思うなら、今のところ、（あみだくじの横棒の数だけ）F9を連打する必要があります。

　あみだくじを考えるなら群論を使えとか、IF関数を使うのであればVBAを使うやり方と大して変わらないのでは？とか、エクセルでない他のプログラミング言語を使った方がよっぽど楽にプロトタイピングをすることができるのに…!?という感想も多々出てくるだろうと思います。

　とはいえ、今日はとりあえず、あみだくじシミュレーションをエクセルでプロトタイピングしてみました。（加減乗除だけで実現したのではない）つまらない実装ですが、（あくまで）暇なときに眺めて遊んで頂ければ、幸いです。

■フルカラー・アナグリフでエクセルのチャート（グラフ）を自然に立体視させるためのコツ　

　暑さをジワジワと感じ始める今頃、いつもエクセル・シミュレーション実習講習会の手伝いをしています。そういうこともあって、この時期、たとえば7月14日に書いた過去記事を眺めてみると、そんな実習講習会の風景や、エクセルの動作・機能・実装を確認しておくために、調査や小ネタ作成などをしていたことを、改めて気づかされます。

　実習講習会は、今回で7年目になります。京都でも一回やりますから、回数でいえば8回やったということで、色々なバージョンのエクセルをそれぞれ独自の使い方をする方々を眺めてきました。当然、日本語ネイティブの人ばかりではありませんから、英語版はもちろん韓国語版やその他の国版のエクセルを使い、それぞれの国の言葉のダイアログ（表現）を眺め、既視感はありつつも実に新鮮な感覚に襲われたりします。

　今年は、昼休みの休憩時間に、自分の実験も兼ねて「エクセルのチャート（グラフ）を赤青（赤シアン）メガネのアナグリフを使うことで、エクセルのチャートを立体的にグリグリ眺めてみよう」という余興（予備実験）をしてみました。参加者やスタッフに赤青（赤シアン）メガネを配り、スクリーンに投影されたエクセルのグラフを立体的に眺めてみたりしたのです。

　やってみてまず気づいたことは、赤シアンメガネだから「（ある程度の）フルカラー」を出すことができるとはいえ、純色の赤色や青色や緑色がチャート（グラフ）の色づけに含まれていると両眼視野闘争が生じてしまうので、チャートの色づけも赤シアンメガネ用の配色にしておくべきだということでした。
　だから、いわゆる「スペクトルカラー風の配色」や「青色から赤色に段階的に色が変わる配色」のチャートはアナグリフ立体表示には使えない、と実感させられました。つまり、フルカラーのアナグリフ用の配色にしたチャートにする必要がある、というわけです。

　今回のような試行錯誤を繰り返して行けば、「フルカラー・アナグリフでエクセルのチャート（グラフ）を、自然に立体視させるためのコツ」を会得することができそうです。来年の今頃には、エクセルで立体動画を眺めることができる、ことを「当たり前田のクラッカー（古い）」にしよう、と考えています。

■エクセルで解く「あみだくじ方程式」と「1次元拡散方程式」　

　「あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる」　from 「n年前へ」

　手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれません。

■エクセル（表計算ソフト）の「表空間と値の拡張」を考える!?　

　エクセル（Microsoft Excel）に「型」を追加する機能が欲しいと思うことがあります。たとえば、複素数やベクトルをひとつのセルで扱ったり、さらにはもっと複雑な属性を持つ「値」を扱いたい、と思うことがあります。

　そうした「（独自の）型」に対して、演算子を自由に定義できたり、セル内での表示方法を自由に定義できたり（「条件付き書式」の自由度が高ければ、独自型の表示スタイルをカスタマイズすることもできるのでしょうか）したい、と思うことがあります。

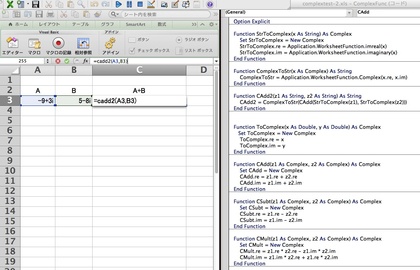　…とそんなことを書いたら、ささっと @IchiroMori さんがシート（コード）を書いて・送ってくれました。「セルに入っている文字列を"imreal"と"imaginary"関数で処理し、独自定義の複素数クラスで処理した上で、"Complex"関数で文字列に戻すというコードです。

　表計算ソフトというものを考えたとき（エクセルは表計算ソフトという範疇にとどまらないものだと思いますが）、表計算ソフトの基本機能は『「表」上で「値」が簡単に計算できる』ということになります。

　そして、そんな表計算ソフトに対して、次の２つの点の拡張をしてみたいと感じることがあります。

１．「表」という部分
　格子状の座標だけでなく、任意の「位置関係」「座標系」「空間」…を使いたい

２．「値」という部分
　任意の属性・特性を持つ「存在（クラス・インスタンスというか）」を扱いたい（属性・値の演算方法やセル・グラフ上での表示方法も含む）

　表計算ソフト（エクセル）の性質『「表」上で「値」が簡単に計算できる』というものを、『空間が各領域で値（属性）を持ち、それらが空間上で作用し合う・作用させ合うことができる』と捉えるならば、その「表」と「値」の拡張ができたなら、一体どんなことができるようになるだろう？と考えたくなります。…空間が各領域で値（属性）を持ち、それらが空間上で作用し合うというのは「世界」持つ基本的な性質ですから、つまりそれは、表計算ソフトが簡単に世界を表現しうるということになります。

　「値」の拡張という部分に関しては、独自クラスを定義した上で文字列にシリアライズ・文字列からデシリアライズすれば可能だろうとは思うのですが、演算子や関数をオーバーロードできないと、既存関数の再利用ができなくなったり、何より「使い勝手」が悪くなるように思います（たとえば、ある属性に対して+=PLUSを定義したとき、その定義がSUM 関数やAVERAGE関数に反映されないと不便ですよね？）。

　…というわけで、表計算ソフトの「表」と「値」の機能拡張ができたなら？と考えるのです。そうすれば、表計算ソフトは、（ある範囲の）世界を表現するのではないかと考えたりするのです。

■エクセルで２次方程式の「解の配置」を図示してみる!?　

　（たとえば）２次方程式、つまりx^2+bx+c==0という方程式の実数解を、中学生か高校生の頃、グラフにしてよく眺めたような気がします。しかし、それらの方程式がいつも１個か２個の解を持つにも関わらず、グラフにして眺めるのは「（時にはゼロ個の）実数解」だったような気がします。

　そこで、今日は「複素数係数を持つ２次方程式の（複素数）解を”可視化する”エクセルシートを作ってみました（ダウンロード先）。"b"と"c"という２つの複素数を入力すると、（ある程度の範囲の）任意の複素数を"x"とした上で"x^2+bx+c"を計算し、その計算結果がゼロ近くになる部分（どんな複素数値を”ｘ”に代入すれば"x^2+bx+c"という式がゼロになるか）を複素平面上で”可視化”する、というエクセルシートです。

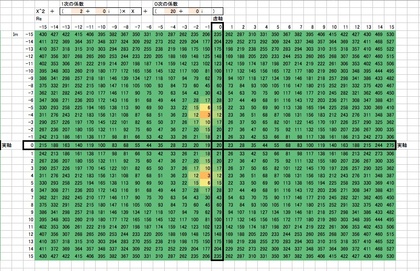
　実数（あるいは時に複素数の）係数b,cを持つ２次方程式の、それら係数b,cを自由自在に動かしてみた時の２次方程式の２つの解（の配置や動き方）を眺めてみると、何だかとても面白いものです。たとえば、実数係数の２次方程式を作った時には、実数軸に線対称な２つの共役数が解になったり、複素数係数を入れてみると…何だか綺麗な対応が見えてきたり…と不思議に魅力的な世界が見えてくるのです。

　明日は、「係数」をドラッグ＆ドロップで動かすと、「解」がどんな風に・どんな配置で動き回るかでも眺めてみよう（眺められるソフトでも作ってみよう）と思います。