2013-12-08[n年前へ]
■「月に引かれてる」のに「反対側も盛り上がる」のはなんで？ 
「月に引かれてる」のに「反対側も盛り上がる」のはなんで？ を書きました。「地球と月が共通重心を
地球と月は、（地球と月を合わせた）共通重心を中心として回転（公転）しています。そんな公転を地球上の各位置が行う時には、地表上の各点は同じ等速の円運動を行い、（その等速円運動する状態を基準とすると）どの点も「月がいる方向とは反対側に働く」同じ大きさの遠心力を受けることになります。
そういうわけで、「月に引かれてる」のに「反対側も盛り上がる」わけです。…あるいは、こんな図を描かなくとも、「月に近い場所ほど強く引っ張られるのだから、月に向かう方向に伸び~るのが当たり前だよね」とも思えるかもしれませんね。
…単純に添付図を描いてみたかったという理由で（あと遠心力の差で月反対側の海が盛り上がるという誤解に対するフォローとして）書いた記事です。
5:38 PM - 8 Dec 13
2015-08-01[n年前へ]
■アムステルダム ゲイ・プライド2015で運河上を「空高く飛ぶフライボード」に驚くの巻
アムステルダムで開催されてるゲイ・プライド2015、その中のイベントのひとつ運河パレードを観に行ってみた。運河を船に乗り進んでいく参加者たちの先頭に立ち、パレード先頭を盛り上げてく「ウォーターシューズ（フライボード）履いて飛び回る人」を見てると、その動きの自由さがたまらなく心地良い。
時に空高く立ち上がり、時には何回かのジャンプを繰り返して上空への加速をつけた後に空中背面回転し…と、地球重力の手から離れていくさまは、まさに「自由」を感じさせます。
I'm through with playing by the rules
of someone else's game.
I'm through accepting limits
'cause someone says they're so.
It's time to try defying gravity.
I think I'll try Defying gravity.
And, you can't pull me down.
Defying Gravity
2018-03-08[n年前へ]
■海沿いの陸地にそそり立つ、ピラミッドのような大古墳
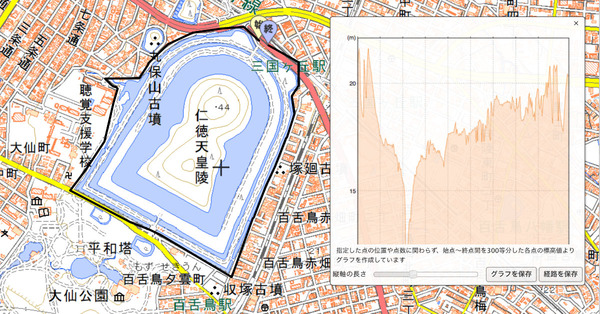
大阪の中百舌鳥近くに行く途中、仁徳天皇陵の一周散歩をしてみる。…すると、天皇陵周りの一周散歩に徒歩で約一時間かかり、その大きさに驚いた。もうひとつ驚いたことが、外堀がパナマ運河みたいに段々が着いていたこと。つまり、不思議に驚かされたことが、仁徳天皇陵の周りにある一番外側の外堀は標高が同じじゃない！ということ。
試しに、国土地理院マップで眺めると、一周をする間の最高・最低値で5ｍくらいの標高差があった。古墳本体を囲う堀は一体化した大きな湖のようで、重力的には等ポテンシャル面を成しているけれど、外堀は同じ標高でない作りになっている。
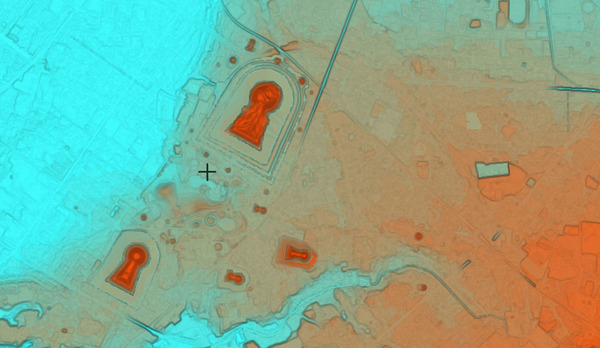
そこで、仁徳天皇陵の「外堀段差」を周囲の地形と一緒に眺めてみる。すると、古墳は、かつての海沿いの傾斜地上に作られていて、その古墳周りに外堀を作ろうとすると、（古墳中央の）水平面とその周囲に段差が作らざるをえない作りになっている。
他の古墳を眺めてみても、まるで水の流れに沿って建つ神社のように、海沿いや川沿いに建っている。…昔の古墳は、海沿いにそそり立つピラミッドのような存在だったのだろうか。
2018-06-27[n年前へ]
■人類が月面上で日常を過ごす時代…それは「あのイタズラが成功する日」かもしれない？
その辺の人（@create_clock） さんのtweetが面白かった。
マンガとかで教室の引き戸に黒板消しを挟んで開けると頭の上に！みたいな描写があるけど、実際にやったことのない人の描写だなと思う。黒板消しの落ちるタイミングが早すぎて頭には当たらない。…確かに、実際にやった過去を振り返ると、黒板消しの落ちるタイミングは早すぎて、誰の頭にも当たらなかった。
10:08 PM - 25 Jun 2018
計算をしてみるとこうなる。教室の入り口の高さは、約2メートル。そこに黒板消しを挟み、ターゲットを待ち構える。ターゲットがドアを開け、身長1.7メートルのターゲットの頭の高さに黒板消しが落ちるまでの時間は、わずか4分の1秒の0.25秒。…そんな短時間に、教室のドアを開け、ドアの真下を通過するのは確かに無理に違いない。
もしも、もうひとつの世界があったとしたらどうだろう？…「教室の引き戸に黒板消しを挟んで開けると頭の上に当たる」…そんなもう一つの世界線、もっと別の場所があったとしたならば、そこは一体どんな場所なんだろうか。
たとえば、教室のドアを開け、ドアの真下に移動するまで、1.5秒掛かるものとしてみる。…もしも、その世界が地球と同じような惑星・密度の場所だとしたら、その惑星の半径は約1900キロメートルという計算になる。そういう星の上で生まれたのなら、「教室の引き戸に黒板消しを挟んで開けると頭の上に落ちる」イタズラができることになる。
もしも、その星の密度が地球と違ったらどうだろう？地表での黒板消しが「頭の高さまで落下する時間」が0.25秒だとして、「教室のドアを開け、ドアの真下に移動するまでの自然な時間、1.5秒」は、ちょうどその6倍に近い。…すると、たとえば、主人公が暮らす世界線がもしも（地球表面比で重力が1/6の）月面上だったとしたら、計算が合うことになる。つまり、教室のドアを開けてから、身長1.7メートルの主人公の頭に黒板消しがあたるまでの時間が、ちょうど1.5秒後…という計算になる。
そうか！そうだったんだ！…ぼくらが昔から眺めたあの景色、「教室の引き戸に黒板消しを挟んで開けると頭の上に落ちる」は決して過去の懐かしい「三丁目の夕日」的な昭和の懐かし風景ではなく、あれは人類が月面上で日常を過ごす遙か未来の日常風景を蜃気楼のように眺めていたに違いない！と気がついた。
そんな発券をしてEureka（エウレカ）！とアルキメデスのように叫び、その瞬間に夢から覚めた。…重力が1/6の世界で、「教室のドアを開けてからわずか1.5秒でドアの真下に移動することは難しい」かもしれない。「教室の引き戸に黒板消しを挟んで開けると頭の上に当たる」…そんなもう一つの世界線は、一体どんな宇宙にあるんだろうか。
」など。