2012-06-25[n年前へ]
2012-06-17[n年前へ]
■「”韓国エステ式レタッチ”はなぜ縮小するとレタッチされていることが丸わかりになってしまうのか？」 
「韓国エステ式レタッチメモ？」から。
韓国エステ式レタッチとは、とくに韓国エステの女性従業員写真によくみられるアニメちっくなPhotoshop修正のことを暫定的にそう呼んでます。･･･（この韓国エステ式レタッチは）縮小すると、なぜかよりわかりやすくなる（レタッチされていることが丸わかりになってしまう）という謎がある。「（人が眺める）視界の広さ」と「大きさの比」とか「画像の周波数特性が自然か」といった「自然・不自然」の問題は、単純かつ奥深いのかもしれません。
韓国エステ式レタッチメモ？
2012-06-14[n年前へ]
■「iOS用Twitterクライアント選抜総選挙投票数分布」を眺めてみる!?
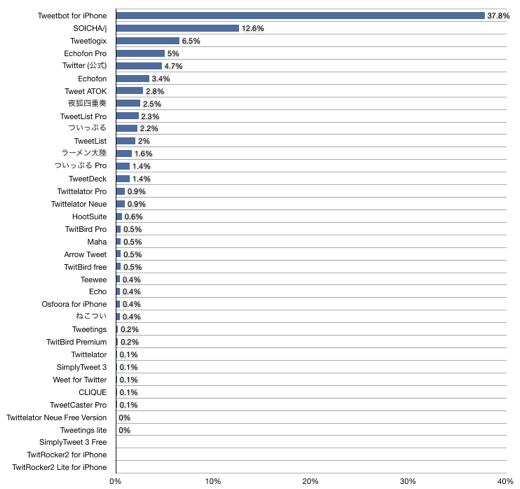「第2回iOS用Twitterクライアント選抜総選挙投票結果」が出ていました。総選挙の得票数分布のグラフが掲載されていたので眺めてみると、有効投票数756票程度であるにも関わらず、冪（べき）乗則に乗っているようです。
（１，２位あたりが冪乗則よりも少し多いようにも見えますが）
2012-06-07[n年前へ]
■「SETIの17年」「乳は父」
今発売中の「月刊星ナビ 2012年7月号」（および次号）に、「（父が）書いた記事”SETIの17年”が掲載されている」と父からメールが来る。…しかし、なぜにATOKは（この文章を打つために）「ちち」と打つと、「乳」を第一候補を出すのだろうか？ 普通、そこは「父」に決まっているだろうに…？
「乳が記事を書く」わけはないのである。父がメールを書くことはあっても、乳がメールを書くなんて話は古今東西聞いたことがないのである。向田邦子だって、「父の詫び状」は書いても､「乳の詫び状」なんて書いてないのだ。おいおい大丈夫か？ATOK。
「ATOKは悪くない」というご意見、多数頂きました。「乳”が”記事を書く」ことはなくとも、「乳”の”記事を書く」ことが多いのではないかとのご指摘…謹んで（特にATOKさまに）お詫び申し上げます。
2012-05-14[n年前へ]
■1m離れ30μmの「大きさ」が見えたら…視力10と呼ぶのです!?
スギ花粉は、およそ直径30μm（マイクロメートル）です。つまり、直径0.5mmのシャーペンの芯の1/10の大きさです。
そのスギ花粉の「大きさ」を、１ｍ離れたところから見ることができる人はいません(存在を見ることはできます)。何しろ、それを（ランドルト環で計る）「視力」に換算すると、視力「１０」というビックリ数値になるくらいです。
身の回りに視力検査で視力１０になったという人がいる…なんてことはありません。「ありえない」ということは、細かな数値を調べるまでもなく、目の大きさや光の波長を思い浮かべるだけで、実に当り前の話です。
アップルによれば、人間の目の解像度では、1メートル離れた直径30マイクロメートル以下のものを見ることができないという。”アップルによれば…という” …この「という」”という”言葉は便利かもしれません。しかし、そんな便利な頻出語句を使うことで書き手が何の理解も消化もしないままに書かれてしまった記事が積み重なっていくことは、デザイン（設計）というものを考える人たち（そうなるかもしれない可能性がある人たち）にとっては、少し残念なことだと思います。
日経BPデザイン『実は「だましのテクニック」を利用しているiPhoneのデザイン』
2012-04-20[n年前へ]
■組み込み向け軽量「mruby」公開
mrubyは組み込みシステム向けに文法をシンプルにし、通常のRubyに比べ少ないメモリーでも動作するようにしたもの。UNIXやLinuxだけでなく、Windows、Mac OS X、BeOSなどでも動作するという。
BeOS…懐かしい。
2012-04-15[n年前へ]
■例外補足で演算子をオーバーロードするエクセルHack！
エクセル（表計算ソフト）の「表空間と値の拡張」を考える!?の続き、エクセルで「複素数」をセルに入力し、"=A+B"といった”普通の記述の”入力で複素数演算を実現させる、という「Excelの独自型」…まず、その実装方法が面白いです。
①複素数セルA1、A2に対し、=A1+A2のように入力
②#VALUE!エラーが出るので、それを検出（Workbook_Changeを利用）
③検出したセルに対し、入力数式を複素数演算用関数を用いた数式に変換（ここは、数式を解析して汎用に変換する機能が必要ですが、これはたぶんできる）
④変換後の専用関数による数式で計算し、そのまま値を返す
この方針を眺めると、 ”エラーを検出し、エラーの元になった文字列をもとに、拡張処理を実行させる”という実装方法が、"No method"例外を補足し、”見つからない”関数名を元にSQLパターン等を生成し、その関数名で「したいこと」を実現するというRuby on Rails のコードを連想します。
例外補足で演算子をオーバーロードする、という面白く・楽しいエクセル Hackです。
2012-04-08[n年前へ]
■エクセルで解く「あみだくじ方程式」と「1次元拡散方程式」
「あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる」 from 「n年前へ」
手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれません。
2012-04-01[n年前へ]
■「科学のブラ」が株式会社トリソプから新発売！
４月１日の「n年前へ」から、『「科学のブラ」が株式会社トリソプから新発売！』
株式会社トリソプが認知心理学を応用した「科学のブラ」を今日発売。キツく寄せて上げる必要もない「女性に優しい」ブラジャーの誕生です。
2012-03-02[n年前へ]
■答がわからない選択問題があったなら？
答がわからない選択問題があったなら？…という「n年前へ」から。
ところで、目の前に、数学の計算問題が置かれていたとして、しかも、その答えがちっともわからないとしたら、あなたなら一体どうすることでしょう？たとえば、それが、4択問題のマークシートなら、…どんなやり方で塗りつぶしを行うでしょう？
そういった分布を示す数値がある時には、ベンフォードの法則が成り立ちます。それは「最初の桁が1である確率は30パーセントにもなる。そして、最初の桁に現れる数字は小さな数値ほど確率が高い」という法則です(２桁以降目の出現分布も導出され、応用されています)。だから、ある時期には、「試験で計算問題を解くことができなかった場合には、「（答えの）最初の桁の数値が１の選択肢を選ぶべし」という科学に裏付けられた（けれど情けない）解法が通用していました。
」など。