hirax.net::Keywords::「バナナの皮」のブログ

■インラインスケートの科学～「転んだ瞬間」の「時間の長さ」　

　インライン・スケートで滑っているとき、路面の段差に気付かずに乗り上げてしまい、車輪がロックし転ぶことがある。平らに見えるアスファルトでも、結構意外なところに凹凸があるもので、路面の先を見ずに滑っているとひっくり返って肘や掌を強く打ちつけてしまい、痛い思いをしたりする。打ち付けるのはたいていの場合「掌」で、それは転んだ瞬間に手で（結局はその先の掌で）身を守ろうとするからである。

　この前転んだ時、「転んだ瞬間」というのは「どれくらいの長さの時間」なのだろうか、と考えた。たとえば、「力いっぱい滑っているときに、いきなり車輪がロックしたら、地面に衝突するまで何秒くらいなのだろう？」と不思議に思ったわけである。そこで、適当に計算してみた結果が下のラクガキになる。

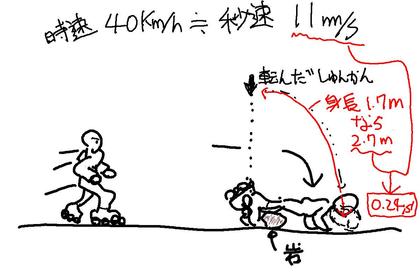
　つまり、とても大雑把に単純化されていて、身長1.7mくらいの人が時速40km≒秒速11mで滑っているときに、いきなり車輪がロックしたとする。そして、足先を中心にして頭の先が秒速11mで（1/4の）円運動をして地面に衝突・・・という状況である。「（1/4の）円周」の長さが、身長1.7mの人ならおよそ2.7mになるので、(秒速11mなら)車輪がロックしてから地面にぶつかるまでは「0.24秒」ということになる。「転んだ瞬間」＝「0.24秒」なのである。短いけれども、転びつつある頭の中では結構長く感じられそうな、微妙な時間である。

　他の場合、たとえば、自転車で全力で走っているとき、バナナの皮の上でコントのように滑ってしまったとき…それぞれの「転んだ瞬間」の「時間の長さ」は一体どのくらいなのだろうか。