2009-04-06[n年前へ]
■インラインスケートの科学～「転んだ瞬間」の「時間の長さ」 
インライン・スケートで滑っているとき、路面の段差に気付かずに乗り上げてしまい、車輪がロックし転ぶことがある。平らに見えるアスファルトでも、結構意外なところに凹凸があるもので、路面の先を見ずに滑っているとひっくり返って肘や掌を強く打ちつけてしまい、痛い思いをしたりする。打ち付けるのはたいていの場合「掌」で、それは転んだ瞬間に手で（結局はその先の掌で）身を守ろうとするからである。
この前転んだ時、「転んだ瞬間」というのは「どれくらいの長さの時間」なのだろうか、と考えた。たとえば、「力いっぱい滑っているときに、いきなり車輪がロックしたら、地面に衝突するまで何秒くらいなのだろう？」と不思議に思ったわけである。そこで、適当に計算してみた結果が下のラクガキになる。
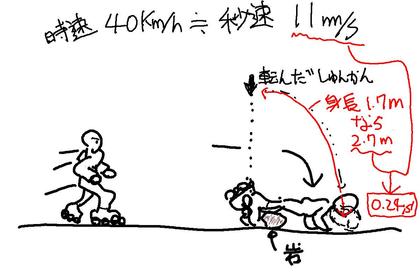
つまり、とても大雑把に単純化されていて、身長1.7mくらいの人が時速40km≒秒速11mで滑っているときに、いきなり車輪がロックしたとする。そして、足先を中心にして頭の先が秒速11mで（1/4の）円運動をして地面に衝突・・・という状況である。「（1/4の）円周」の長さが、身長1.7mの人ならおよそ2.7mになるので、(秒速11mなら)車輪がロックしてから地面にぶつかるまでは「0.24秒」ということになる。「転んだ瞬間」＝「0.24秒」なのである。短いけれども、転びつつある頭の中では結構長く感じられそうな、微妙な時間である。
他の場合、たとえば、自転車で全力で走っているとき、バナナの皮の上でコントのように滑ってしまったとき…それぞれの「転んだ瞬間」の「時間の長さ」は一体どのくらいなのだろうか。
2009-06-02[n年前へ]
■「楕円上を動くふたつの円」で考える「ブラのカップサイズ」
「楕円の周上」に中心を持つ２つの円が、その「楕円の周上」を動くとき、二つの円の位置を変数として、「楕円の周長」と「楕円および２つの円を囲む曲線の中で長さが最小となるものの曲線長」の「差」を求めなさい、・・・という問題があったとする。これは、もちろん立派な数学（算数）の問題である。二つの円の位置を変数とした、一種の最小化問題である。
しかし、下の図（人の胸部部分を単純化した断面図）とともに、そしてこのサイトhirax.net上で上記の「問題文」を眺めると、この問題の趣は少し変わる。上記の問題文が意図するところは、こうだ。「胴体のどこにふたつのバスト（＝円）が位置するかで決まる、アンダーバストとトップバストの差、すなわちブラジャーのカップサイズを求めよ」という問題に変わるのである。
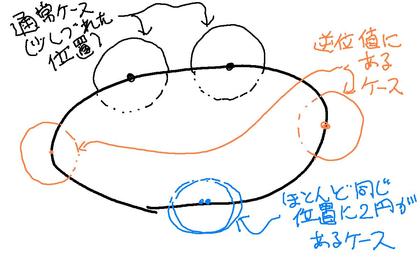
つまり、この問題文はブラジャーのカップサイズの「最適化問題」なのだ。この「最適化」は、人によって、「最大化」指向（嗜好）の場合もあるだろうし、あるいは「最小化」指向（嗜好）の場合もあるかもしれない。しかし、いずれの場合にせよ、この問いは「単純化したバストにおけるブラジャーのカップサイズの最適化問題」なのだ。
さて、図を見れば、そして少し考えればわかるように、このモデルでは（トップバストとアンダーバストの長さの差から決まる）ブラジャーのカップサイズは、二つのバストが反対位置にあるときに最大の値をとる。つまり、ふたつの胸は離れていれば離れているほど、カップサイズは大きくなる。極端な話、たとえば、両脇の下に胸があったりしたら、ブラジャーのカップサイズが大きくなるのである
こんな風に、つらつらと考えてみると、なるほどごく単純な楕円と円だけを材料に作った算数の問題でさえ、なんと奥が深いのだろう！と感嘆する人も多いのではないだろうか。・・・そんなわけないか。
2012-11-05[n年前へ]
■日常生活で役立つ数学の問題「マンション駐輪場割り当て数の将来予測」編
マンションの理事会や管理委員の役職番が回ってきたりすると、マンションの駐輪場の「割り当て数」について頭を悩ませたりすることがあります。たとえば、面積が限られているスペースに、自転車置き場とオートバイ置き場を作らねばならない…けれど、その比率は一体どのようにしたら良いかわからない…といったこともあると思います。
あなたが住んでいるマンションが、１００戸入居できる新築マンションで、けれどまだ10世帯しか入居しておらず、その入居済み10世帯の中でオートバイを持っているのは１世帯でたった１台だけだったとします。
残り90戸の入居がまだ行われていない現時点で、「バイク置き場」の個数を決めてしまわなければならないとしたら、あなたは一体何台程度バイクを置くことができるようにしたら良いものでしょうか？
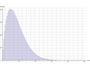
「世帯はバイクを１台しか持つことはない」ものとして、"10世帯の中でオートバイを持っているのは「1世帯たった１台」だけだった"ということをもとにして、世帯がバイクを持つ確率pの（さらに）確率分布を(逆算して)求めてみたのが下のグラフです。
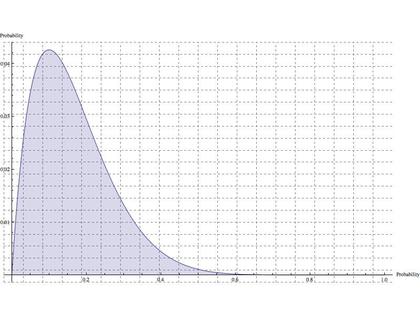
このグラフを眺めてみると、各戸がバイクを持っている確率としては、「確率が一番高いのは1/10程度だけれども、バイクを持つ確率は、それより実は結構高いのかもね」という具合になっています。そして、バイクを持つ確率が上のグラフのような場合に、さらに「100戸全て入居済みになった時点でのバイク保有数予測」をしてみたのが次(下)のグラフです。
10戸入居時点でバイクが１台だけだったから、全部で100戸のマンションならトータル１０台のバイク置き場を用意しておけばいいかなと思ったら…わっ！バイク置き場が全然足りない事態になってしまった ！？と冷や汗をかくことになりそうです。
日常生活の中では、こんな「ご近所さんの間ですったもんだしがちな割り当て数に関する難問題」に出会うことも頻繁にありそうな気がします。…なんていう風に考え出すと、あぁ学校の勉強をもっと真面目にやっておけば良かった…（泣）と思ったりしそう、です。
」など。