2018-06-17[n年前へ]
■「逆上がり」を「自然にできる」ための物理学的メソッド 
 胸ほどの高さにある鉄棒をつかみ、地面を蹴って鉄棒の上に回り込むのが「逆上がり」。慣れると簡単にできますが、一番最初は、なかなか回れず「運動なんかキライだ!」と感じてしまったりするものです。
胸ほどの高さにある鉄棒をつかみ、地面を蹴って鉄棒の上に回り込むのが「逆上がり」。慣れると簡単にできますが、一番最初は、なかなか回れず「運動なんかキライだ!」と感じてしまったりするものです。
よく「学校で勉強することなんて日常生活ではほぼ役に立たない」と言われたりしますが、たとえば「自然がどのような振る舞いを示すかを可能な限り簡易に説明する」のが、たとえば、物理だったりします。…というわけで、今日は、「逆上がり」を「自然にできる」ための物理学的メソッドを考えてみることにします。
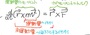
 まず、回転の運動方程式を思い浮かべれば(右図)、逆上がりを成功させるためには、まずはシンプルに地面を蹴る瞬間に回転のイキオイを最大化したくなります。
まず、回転の運動方程式を思い浮かべれば(右図)、逆上がりを成功させるためには、まずはシンプルに地面を蹴る瞬間に回転のイキオイを最大化したくなります。
運動量のモーメント(角運動量)が、大雑把には、回転原点(ここでは単純のために鉄棒位置としておきましょう)と蹴り上げる足が持つ運動量の外積であること、つまり、その大きさが「鉄棒から足先」と「足の運動量」からなる平行四辺形の面積を考えると、それを最大化するために必要なことは「足を蹴り上げる方向は鉛直上方向ではなくて、平行四辺形が直角形となる「斜め上」であることがわかります。つまり、必要なことは「上に高く飛ぶ」ではなく「足を前上方に蹴り上げる」ことだということになります。

もちろん、蹴り上げる際の「足の運動量」を最大化することも重要でしょう。ということは、たとえばサッカーでボールを蹴る「利き足」を「前上方向に蹴り上げられる側の足」にするということも効果的なはずです。つまり、サッカーでボールを蹴り上げるのと同じ動きで、利き足を上に蹴り上げて、その回転を行う運動モーメントを逆上がりの原動力とするわけです。
あるいは、それを言い換えれば、まずは「鉄棒の下に、非利き足で踏み込んだ上で、利き足を斜め前方上に蹴り上げる」というルーチーンが、自然に逆上がりを成功させるための動きとなるわけです。
大人の男性なら蹴り上げる時の足の速度は秒速15メートル(時速55キロメートル)程度です。この速度で人の体を単純化して計算してみると、上記の蹴り方をすれば、確かに逆上がりが成功する結果となります。
ちなみに、サッカー選手なら足を蹴り上げる速度は時速100キロメートルを越えたりします。 サッカーのワールドカップが開催されている今日この頃、サッカー選手の「逆上がり」を見てみたくなります。